Phần tự luận (8 điểm) SVIP

Hướng dẫn giải:

a) $M=\sqrt{75}-\sqrt{12}-\sqrt{48}+\sqrt{3}.$

$M=\sqrt{{{5}^{2}}.3}-\sqrt{{{2}^{2}}.3}-\sqrt{{{4}^{2}}.3}+\sqrt{3}$

$M=5\sqrt{3}-2\sqrt{3}-4\sqrt{3}+\sqrt{3}$

$M=0$.

Vậy biểu thức $M=0$.

b) Với điều kiện $x\ge 0;$ $x\ne 1$ biểu thức $P$ được biến đổi tương đương như sau:

$P=\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{3}{\sqrt{x}+1}-\dfrac{4\sqrt{x}-3}{x-1}$

$\Leftrightarrow \,P=\dfrac{\sqrt{x}\left( \sqrt{x}+1 \right)}{\left( \sqrt{x}-1 \right)\left( \sqrt{x}+1 \right)}+\dfrac{3\left( \sqrt{x}-1 \right)}{\left( \sqrt{x}+1 \right)\left( \sqrt{x}-1 \right)}-\dfrac{4\sqrt{x}-3}{\left( \sqrt{x}-1 \right)\left( \sqrt{x}+1 \right)}$

$\Leftrightarrow \,P=\dfrac{x+\sqrt{x}+3\sqrt{x}-3-4\sqrt{x}+3}{\left( \sqrt{x}-1 \right)\left( \sqrt{x}+1 \right)}$

$\Leftrightarrow \,P=\dfrac{x}{x-1}$.

Vậy với $x\ge 0;$ $x\ne 1$ thì $P=\dfrac{x}{x-1}$.

Hướng dẫn giải:

a) Cách 1: ${{x}^{2}}+5x-6=0$ $\Leftrightarrow \,{{x}^{2}}-x+6x-6=0$

$\Leftrightarrow \,x(x-1)+6(x-1)=0$ $\Leftrightarrow \,(x-1)(x+6)=0$

$\Leftrightarrow \,\left[ \begin{aligned} & x-1=0 \\ & x+6=0 \\ \end{aligned} \right.$ $\Leftrightarrow \,\left[ \begin{aligned} & x=1 \\ & x=-6 \\ \end{aligned} \right.$

Vậy phương trình có nghiệm $x\in \left\{ -6;\,1 \right\}$.

Cách 2: Xét phương trình ${{x}^{2}}+5x-6=0$ có hệ số $a=1;\,b=5;\,c=-6$.

Ta có $a+b+c=1+5+(-6)=0$.

$\Rightarrow $ Phương trình có hai nghiệm ${{x}_{1}}=1;\,{{x}_{2}}=\dfrac{c}{a}=-6$.

Vậy phương trình có nghiệm $x\in \left\{ -6;\,1 \right\}$.

b) Xét phương trình ${{x}^{2}}-2mx+4m-4=0$ $(1)$.

Có $\Delta ={{\left( -2m \right)}^{2}}-4(4m-4)=4{{m}^{2}}-16m+16=4{{(m-2)}^{2}}$.

Để phương trình $(1)$ có hai nghiệm ${{x}_{1}},$ ${{x}_{2}}$ khi và chỉ khi $\Delta \ge 0$

$\Leftrightarrow 4{{(m-2)}^{2}}\ge 0$ luôn đúng với mọi giá trị của $m$.

Theo hệ thức Vi-et ta có: $\left\{ \begin{aligned} & {{x}_{1}}+{{x}_{2}}=2m \\ & {{x}_{1}}.{{x}_{2}}=4m-4 \\ \end{aligned} \right.$.

Theo đề bài ta có ${{x}_{1}}^{2}+{{x}_{2}}^{2}-8=0$ $\Leftrightarrow \,{{\left( {{x}_{1}}+{{x}_{2}} \right)}^{2}}-2{{x}_{1}}{{x}_{2}}-8=0$

$\Leftrightarrow \,{{\left( 2m \right)}^{2}}-2\left( 4m-4 \right)-8=0$ $\Leftrightarrow \,4{{m}^{2}}-8m=0$ $\Leftrightarrow \,4m(m-2)=0$

$\Leftrightarrow \,\left[ \begin{aligned} & m=0 \\ & m-2=0 \\ \end{aligned} \right.$ $\Leftrightarrow \,\left[ \begin{aligned} & m=0 \\ & m=2 \\ \end{aligned} \right.$ (thỏa mãn điều kiện).

Vậy với $m=0$ hoặc $m=2$ thì phương trình ${{x}^{2}}-2mx+4m-4=0$ có hai nghiệm ${{x}_{1}},$ ${{x}_{2}}$ thỏa mãn ${{x}_{1}}^{2}+{{x}_{2}}^{2}-8=0.$

Hướng dẫn giải:

Gọi số hồ sơ đăng kí trực tuyến là $x$ (hồ sơ), điều kiện $x\in \mathbb{N}^*,\,x<650$.

Vì trường THPT nhận được $650$ hồ sơ nên số hồ sơ đăng kí trực tiếp tại nhà trường là $650-x$ (hồ sơ).

Theo đề bài, số hồ sơ đăng kí trực tuyến nhiều hơn số hồ sơ đăng kí trực tiếp là $120$ hồ sơ nên ta có phương trình:

$x-\left( 650-x \right)=120$ $\Leftrightarrow \,2x-650=120$

$\Leftrightarrow \,2x=770$ $\Leftrightarrow \,x=385$ (thỏa mãn điều kiện).

Vậy số hồ sơ đăng kí trực tuyến là $385$ hồ sơ.

Hướng dẫn giải:

a) Theo giả thiết, $AM,$ $AN$ là các tiếp tuyến của đường tròn $\left( I \right)$ với $M,$ $N$ là các tiếp điểm.

$\Rightarrow $ $\widehat{AMI}=\widehat{ANI}={{90}^{\circ}}$.

Xét tứ giác $AMIN$ có $\widehat{AMI}+\widehat{ANI}={{90}^{\circ}}+{{90}^{\circ}}={{180}^{\circ}}$, mà $\widehat{AMI}$ và $\widehat{ANI}$ là hai góc ở vị trí đối diện nhau.

Suy ra tứ giác $AMIN$ nội tiếp đường tròn (dấu hiệu nhận biết).

Vậy tứ giác $AMIN$ nội tiếp đường tròn.

b) 

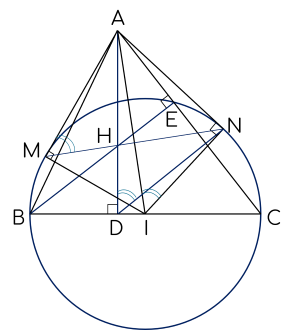
Theo giả thiết $AD$ là đường cao của $\Delta ABC$

$\Rightarrow \,AD\bot BC$ hay $\widehat{ADI}={{90}^{\circ}}$.

Xét tứ giác $ADIN$ có $\widehat{ADI}+\widehat{ANI}={{90}^{\circ}}+{{90}^{\circ}}={{180}^{\circ}}$, mà hai góc $\widehat{ADI}$ và $\widehat{ANI}$ ở vị trí đối diện nhau.

$\Rightarrow $ tứ giác $ADIN$ nội tiếp đường tròn (dấu hiệu nhận biết).

$\Rightarrow $ $\widehat{ADN}=\widehat{AIN}$ (góc nội tiếp cùng chắn cung $\overset\frown{AN}$) $(1)$

Theo câu (a), tứ giác $AMIN$ nội tiếp đường tròn

$\Rightarrow \widehat{AMN}=\widehat{AIN}$ (góc nội tiếp cùng chắn cung $\overset\frown{AN}$) $(2)$

Từ $(1)$ và $(2)$ suy ra $\widehat{AMN}=\widehat{ADN}$.

Gọi $E$ là chân đường cao hạ từ $B$ xuống $AC$, $BE\bot AC$

$\Rightarrow \,\widehat{AEH}={{90}^{\circ}}$.

Xét $\Delta AEH$ và $\Delta ADC$ có:

$\widehat{DAC} $ chung;

$\widehat{AEH}=\widehat{ADC}={{90}^{\circ}}$

$\Rightarrow \,\Delta AEH\backsim\Delta ADC$ (g-g).

$\Rightarrow \,\dfrac{AH}{AC}=\dfrac{AE}{AD}$

$\Rightarrow \,AH.AD=AC.AE$ (3)

Xét $\Delta AEN$ và $\Delta ANC$ có:

$\widehat{EAN}$ chung;

$\widehat{ANE}=\widehat{ACN}$ (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung $\overset\frown{EN}$)

$\Rightarrow \,\Delta AEN\backsim\Delta ANC$ (g-g)

$\Rightarrow \,\dfrac{AE}{AN}=\dfrac{AN}{AC}$

$\Rightarrow \,AC.AE=A{{N}^{2}}$ (4)

Từ (3) và (4) suy ra $AH.AD=A{{N}^{2}}$

$\Rightarrow \,\dfrac{AH}{AN}=\dfrac{AN}{AD}$.

Xét $\Delta AHN$ và $\Delta AND$ có:

$\widehat{HAN}$ chung;

$\dfrac{AH}{AN}=\dfrac{AN}{AD}$ (cmt).

$\Rightarrow \Delta AHN\backsim\Delta AND$ (c-g-c)

$\Rightarrow \widehat{AHN}=\widehat{AND}$ (đpcm).

c)Ta có $\widehat{AMN}=\widehat{ANM}$ (hai góc tạo bởi tiếp tuyến và dây cung cùng chắn cung $\overset\frown{MN}$ của $\left( I \right)$).

$\Rightarrow \,\widehat{ANM}=\widehat{ADN}$.

Theo câu (b), ta có $\Delta AHN\backsim\Delta AND$.

$\Rightarrow \,\widehat{ANH}=\widehat{ADN}$

$\Rightarrow \,\widehat{ANH}=\widehat{ANM}$, mà $H,$ $M$ nằm cùng phía với $AN$.

$\Rightarrow$ Ba điểm $H,M,N$ thẳng hàng.

Hướng dẫn giải:

Gọi $M(a;\,{{a}^{2}})\in (P)$ với $-3<a<2$.

Gọi $H,\,K,\,I$ lần lượt là hình chiếu của $A,\,B,\,M$ lên trục $Ox$.

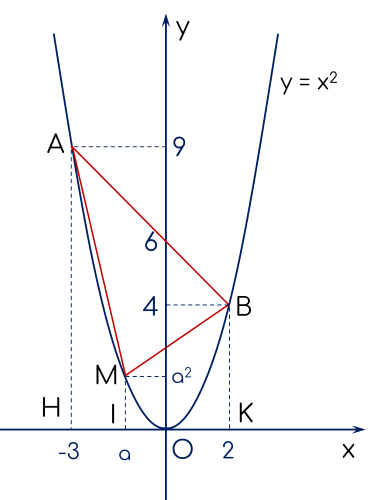
Diện tích tam giác $MAB$ được xác định là:

${{S}_{\Delta MAB}}={{S}_{ABKH}}-{{S}_{AMIH}}-{{S}_{BMIK}}$

$=\dfrac{1}{2}(9+4).5-\dfrac{1}{2}(9+{{a}^{2}}).\left| -3-a \right|-\dfrac{1}{2}(4+{{a}^{2}}).\left| 2-a \right|$

$=\dfrac{65}{2}-\dfrac{1}{2}(9+{{a}^{2}}).\left| -3-a \right|-\dfrac{1}{2}(4+{{a}^{2}}).\left| 2-a \right|$.

Vì $-3<a<2$ nên ta có $\left\{ \begin{aligned} & a+3>0 \\ & 2-a>0 \\ \end{aligned} \right.$$\Rightarrow \,\left\{ \begin{aligned} & \left| -3-a \right|=a+3 \\ & \left| 2-a \right|=2-a \\ \end{aligned} \right.$.

Khi đó ta có: ${{S}_{\Delta MAB}}=\dfrac{65}{2}-\dfrac{1}{2}(9+{{a}^{2}}).(a+3)-\dfrac{1}{2}(4+{{a}^{2}}).(2-a)$

$=\dfrac{65}{2}-\dfrac{1}{2}\left[ (9+{{a}^{2}}).(a+3)+(4+{{a}^{2}}).(2-a) \right]$

$=\dfrac{65}{2}-\dfrac{1}{2}\left( 9a+27+{{a}^{3}}+3{{a}^{2}}+8-4a+2{{a}^{2}}-{{a}^{3}} \right)$

$=\dfrac{65}{2}-\dfrac{1}{2}\left( 5{{a}^{2}}+5a+35 \right)$

$=\dfrac{65}{2}-\dfrac{5}{2}\left( {{a}^{2}}+a+7 \right)$.

Xét ${{a}^{2}}+a+7={{a}^{2}}+2.a.\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{27}{4}={{\left( a+\dfrac{1}{2} \right)}^{2}}+\dfrac{27}{4}\ge \dfrac{27}{4}$

$\Rightarrow \,{{S}_{\Delta MAB}}\le \dfrac{65}{2}-\dfrac{5}{2}.\dfrac{27}{4}=\dfrac{125}{8}$.

Vậy giá trị lớn nhất của diện tích tam giác $MAB$ là $\dfrac{125}{8}$, đạt được khi $a=-\dfrac{1}{2}$, tọa độ của điểm$\,M\left(-\dfrac{1}{2};\,\dfrac{1}{4}\right)$.