Tự luận (3 điểm) SVIP

Hướng dẫn giải:

Gọi $a$ là số tiền vay (triệu đồng), $r$ là lãi suất, $m$ là số tiền hàng tháng trả (triệu đồng).

Số tiền nợ sau tháng thứ nhất là: $N_1=a(1+r )-m$.

Số tiền nợ sau tháng thứ hai là: ${{N}_{2}}=\left[ a(1+r )-m \right]+\left[ a(1-r )-m \right]r-m$

$=a{{(1+r )}^{2}}-m\left[ (1+r )+1 \right]$

….

Số tiền nợ sau $n$ tháng là:

${{N}_{n}}=a{{(1+r )}^{n}}-m\left[ {{(1+r )}^{n-1}}+{{(1+r )}^{n-2}}+...+1 \right]=a{{(1+r )}^{n}}-m\dfrac{{{(1+r )}^{n}}-1}{r}$.

Sau $n$ tháng anh Nam trả hết nợ:

${{N}_{n}}=a{{(1+r )}^{n}}-m\dfrac{{{(1+r )}^{n}}-1}{r}=0$

$\Leftrightarrow 1000{{(1+0,005 )}^{n}}-30\dfrac{{{(1+0,005 )}^{n}}-1}{0,005}=0$

$\Leftrightarrow n=36,55$

Vậy $37$ tháng thì anh Nam trả hết nợ.

Hướng dẫn giải:

 Hình chóp $S.ABCD$ có đường cao $h=\dfrac{\sqrt{2}}{2}$.

Ta có ${{V}_{S.AMC}}=\dfrac{1}{3}{{S}_{\Delta AMN}}.h$

$=\dfrac{\sqrt{2}}{6}.{{S}_{\Delta AMN}}$.

Thể tích khối tứ diện $S.AMN$ đạt giá trị nhỏ nhất khi ${{S}_{\Delta AMN}}$ nhỏ nhất.

Đặt $x=CM,y=NC$

$\Rightarrow MB=1-x,DN=1-y$

Ta có ${{x}^{2}}+{{y}^{2}}=1\Leftrightarrow xy=\dfrac{{{(x+y)}^{2}}-1}{2}$

Với ${{(x+y)}^{2}}\le 2({{x}^{2}}+{{y}^{2}})\Rightarrow 1<x+y\le \sqrt{2}$.

Ta có ${{S}_{\Delta AMN}}=1-{{S}_{\Delta ABM}}-{{S}_{\Delta CMN}}-{{S}_{\Delta ADN}}$

$=1-\dfrac{1}{2}(1-x)-\dfrac{1}{2}x.y-\dfrac{1}{2}.(1-y)$

$=1-\dfrac{1-x}{2}-\dfrac{x.y}{2}-\dfrac{1-y}{2}$

$=\dfrac{1}{2}\Big((x+y)-\dfrac{{{(x+y)}^{2}}}{2}+\dfrac{1}{2}\Big)$.

Đặt $t=x+y\Rightarrow {{S}_{\Delta AMN}}=-\dfrac{1}{4}{{t}^{2}}+\dfrac{1}{2}t+\dfrac{1}{4}$.

Tam giác có diện tích nhỏ nhất là:

${{S}_{\min }}=\dfrac{2\sqrt{2}-1}{4}$ khi $t=\sqrt{2}$.

Vậy thể tích nhỏ nhất của tứ diện $S.AMN$ là:

${{V}_{\min }}=\dfrac{\sqrt{2}}{6}.\dfrac{2\sqrt{2}-1}{4}=\dfrac{4-\sqrt{2}}{24}$.

Hướng dẫn giải:

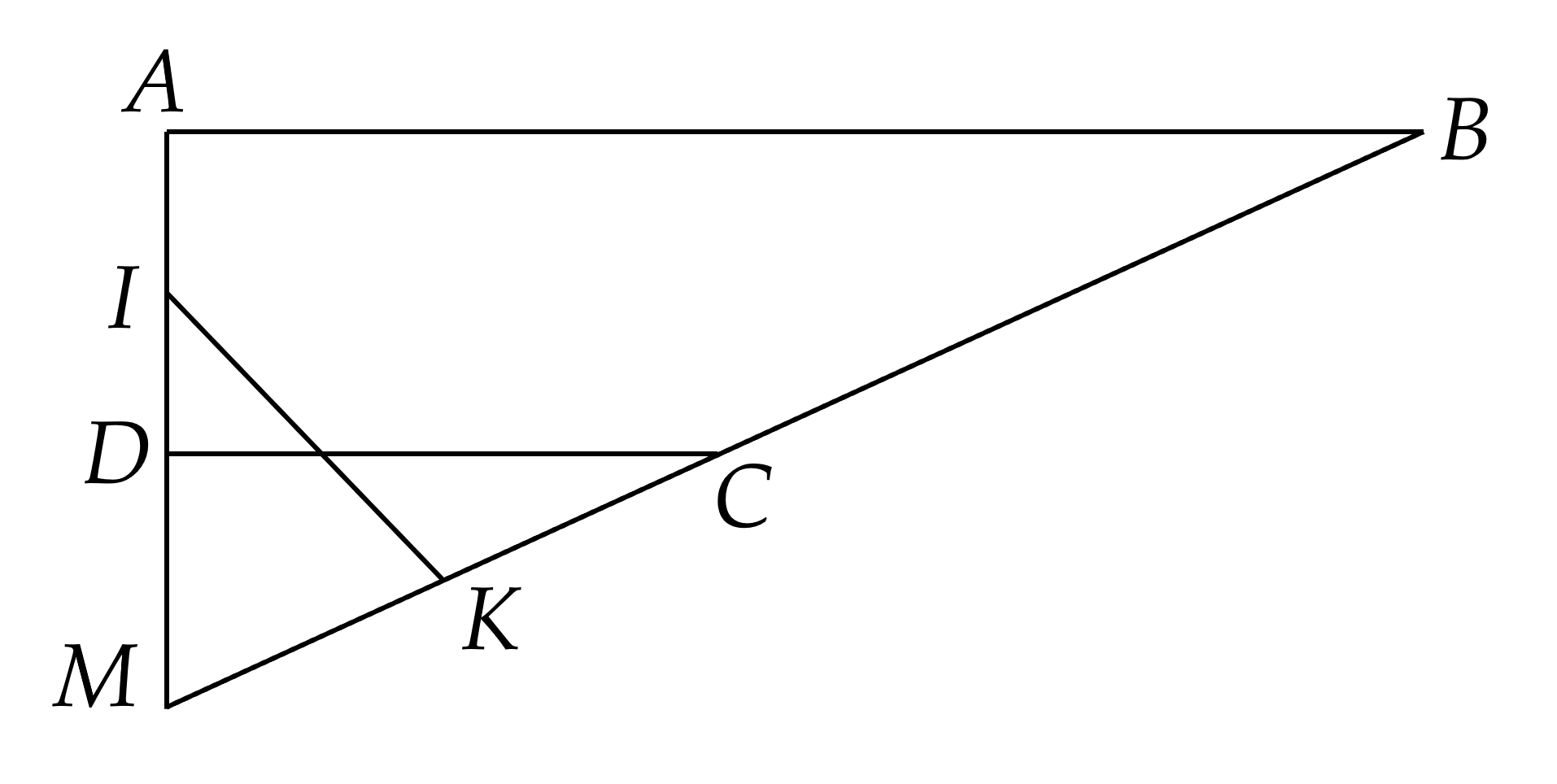
 Kẻ $IK\bot BC\,(K\in BC)\Rightarrow ((SBC);(ABCD))=\widehat{SKI}=60^\circ$

Gọi $M=AD\cap BC$.

Ta có $\dfrac{MD}{MA}=\dfrac{1}{3}\Rightarrow MD=\dfrac{a}{2}$

Ta có $\Delta MIK$ đồng dạng với $\Delta MBA$ nên suy ra

$\dfrac{IK}{BA}=\dfrac{MI}{MB}=\dfrac{a}{\sqrt{{{(3a)}^{2}}+{{(\dfrac{3a}{2})}^{2}}}}=\dfrac{2\sqrt{5}}{15}$

$\Rightarrow IK=\dfrac{2\sqrt{5}}{15}.3a=\dfrac{2a\sqrt{5}}{5}$

Gọi $N$ là trung điểm của $SD$.

Ta có $d(N,(SBC))=\dfrac{1}{2}d(D,(SBC))=\dfrac{1}{4}d(I,(SBC))$

Từ $I$ kẻ $IH\bot SK$ suy ra

$IH=d(I,(SBC))=IK.\sin {{60}^{0}}=\dfrac{a\sqrt{15}}{5}$

$\Rightarrow d(N,(SBC))=\dfrac{a\sqrt{15}}{20}$