 File: 17136207288062370288475005508247.jpg
File: 17136207288062370288475005508247.jpg
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





a: \(\text{Δ}=\left(2m+1\right)^2-4\cdot\left(m^2+\dfrac{1}{2}\right)\)
\(=4m^2+4m+1-4m^2-2=4m-1\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
=>4m-1>0
=>m>1/4
b: Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m+1\\x_1x_2=\dfrac{c}{a}=m^2+\dfrac{1}{2}\end{matrix}\right.\)
\(M=\left(x_1-1\right)\left(x_2-1\right)\)
\(=x_1x_2-\left(x_1+x_2\right)+1\)
\(=m^2+\dfrac{1}{2}-2m-1+1\)
\(=m^2-2m+\dfrac{1}{2}\)
\(=m^2-2m+1-\dfrac{1}{2}=\left(m-1\right)^2-\dfrac{1}{2}>=-\dfrac{1}{2}\forall m\)
Dấu '=' xảy ra khi m-1=0
=>m=1(nhận


a: Xét (O) có
ΔBFC nội tiếp
BC là đường kính
Do đó:ΔBFC vuông tại F
=>CF\(\perp\)AB tại F
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>BE\(\perp\)AC tại E
Xét tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=90^0+90^0=180^0\)
nên AEHF là tứ giác nội tiếp

Δ'=4-m-5=-m-1
để pt có 2 nghiệm phân biệt :Δ'>0 ⇒-m-1>0 ⇔-m>1 ⇔m<-1
áp dụng hệ thức vi ét :
x1+x2=4
x1x2=m+5
x12+x1x2+2x1=2x(x mấy đây ko có sao làm)2-4x2
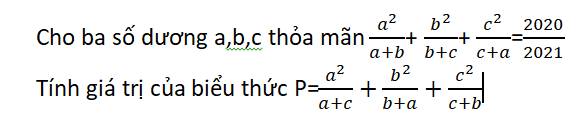
 Giúp mình câu C với ạ
Giúp mình câu C với ạ 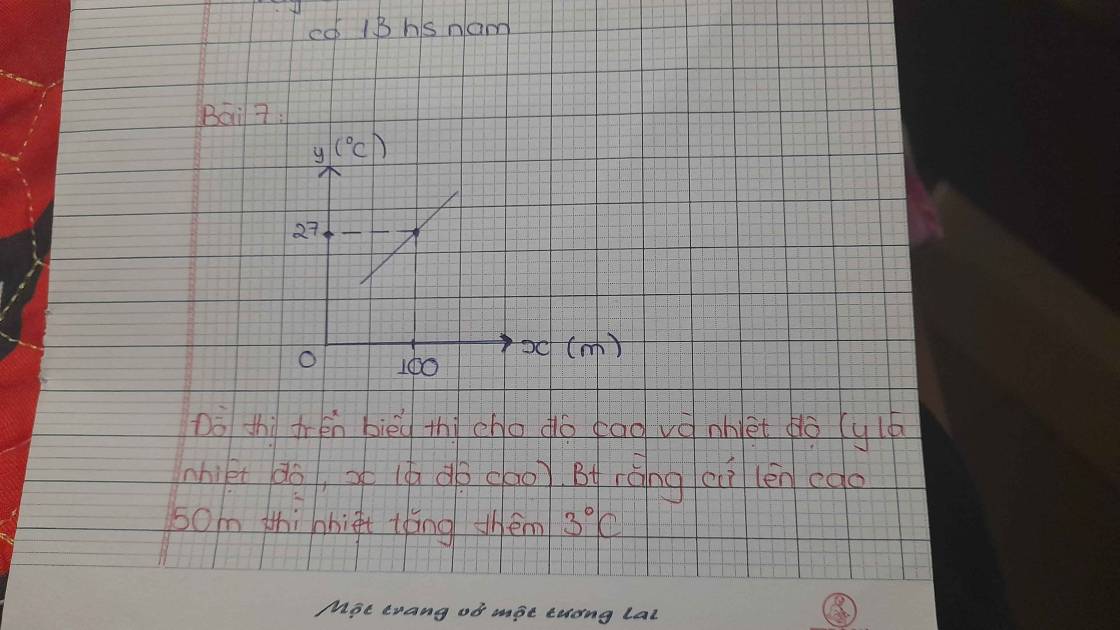

\(\text{Δ}=\left(m+3\right)^2-4\left(m-1\right)\)
\(=m^2+6m+9-4m+4\)
\(=m^2+2m+13=\left(m+1\right)^2+12>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=m+3\\x_1x_2=\dfrac{c}{a}=m-1\end{matrix}\right.\)
\(x_1< \dfrac{1}{2}< x_2\)
=>\(\left(x_1-\dfrac{1}{2}\right)\left(x_2-\dfrac{1}{2}\right)< 0\)
=>\(x_1x_2-\dfrac{1}{2}\left(x_1+x_2\right)+\dfrac{1}{4}< 0\)
=>\(m-1-\dfrac{1}{2}\left(m+3\right)+\dfrac{1}{4}< 0\)
=>\(m-\dfrac{3}{4}-\dfrac{1}{2}m-\dfrac{3}{2}< 0\)
=>\(\dfrac{1}{2}m< \dfrac{3}{2}+\dfrac{3}{4}=\dfrac{9}{4}\)
=>\(m< \dfrac{9}{4}\cdot2=\dfrac{9}{2}\)