a: Thay a=3 vào (P), ta được:

\(y=a\cdot x^2=3x^2\)

Vẽ đồ thị:

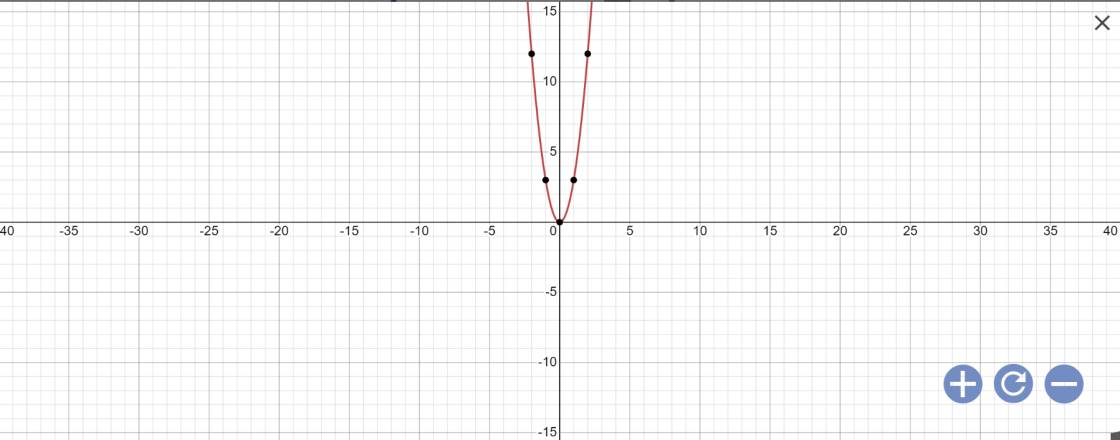
b: Thay x=2 và \(y=-\dfrac{5}{4}\) vào (P), ta được:

\(a\cdot2^2=-\dfrac{5}{4}\)

=>\(a\cdot4=-\dfrac{5}{4}\)

=>\(a=-\dfrac{5}{4}:4=-\dfrac{5}{16}\)

a: Xét tứ giác MAOB có \(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)

nên MAOB là tứ giác nội tiếp

b: Xét (O) có

\(\widehat{MAE}\) là góc tạo bởi tiếp tuyến AM và dây cung AE

\(\widehat{ADE}\) là góc nội tiếp chắn cung AE

Do đó: \(\widehat{MAE}=\widehat{ADE}\)

mà \(\widehat{ADE}=\widehat{FME}\)(hai góc so le trong, BM//AD)

nên \(\widehat{FME}=\widehat{FAM}\)

Xét ΔFME và ΔFAM có

\(\widehat{FME}=\widehat{FAM}\)

\(\widehat{MFE}\) chung

Do đó: ΔFME~ΔFAM

=>\(\dfrac{FM}{FA}=\dfrac{FE}{FM}\)

=>\(FM^2=FA\cdot FE\)

c: Xét (O) có

\(\widehat{FBE}\) là góc tạo bởi tiếp tuyến BF và dây cung BE

\(\widehat{BAE}\) là góc nội tiếp chắn cung BE

Do đó: \(\widehat{FBE}=\widehat{BAE}\)

Xét ΔFBE và ΔFAB có

\(\widehat{FBE}=\widehat{FAB}\)

\(\widehat{BFE}\) chung

Do đó: ΔFBE~ΔFAB

=>\(\dfrac{FB}{FA}=\dfrac{FE}{FB}\)

=>\(FB^2=FA\cdot FE\)

=>\(FB^2=FM^2\)

=>FB=FM

=>F là trung điểm của MB

Gọi giá tiền của máy lạnh sau khi giảm giá là x(đồng), giá tiền của chiếc tivi sau khi giảm giá là y(đồng)

(Điều kiện: x>0; y>0)

Số tiền bác Nam phải trả trong thực tế là 28300000 nên x+y=28300000(1)

Giá ban đầu của 1 chiếc máy lạnh là \(x:\left(1-5\%\right)=x:95\%=x:\dfrac{19}{20}=\dfrac{20}{19}x\left(đồng\right)\)

Giá ban đầu của 1 chiếc tivi là:

\(y:\left(1-20\%\right)=y:0,8=y:\dfrac{4}{5}=\dfrac{5}{4}y\left(đồng\right)\)

Tổng số tiền phải trả ban đầu là 32000000 nên \(\dfrac{20}{19}x+\dfrac{5}{4}y=32000000\left(2\right)\)

Từ (1) và (2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}x+y=28300000\\\dfrac{20}{19}x+\dfrac{5}{4}y=32000000\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\dfrac{5}{4}x+\dfrac{5}{4}y=35375000\\\dfrac{20}{19}x+\dfrac{5}{4}y=32000000\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\dfrac{15}{76}x=3375000\\x+y=28300000\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=17100000\\y=11200000\end{matrix}\right.\left(nhận\right)\)

Vậy: giá tiền của máy lạnh sau khi giảm giá là 17100000(đồng), giá tiền của chiếc tivi sau khi giảm giá là 11200000(đồng)

Xét (O) có

ΔACB nội tiếp

AB là đường kính

Do đó: ΔACB vuông tại C

=>BC\(\perp\)AK tại C

Xét tứ giác BHCK có \(\widehat{BHK}=\widehat{BCK}=90^0\)

nên BHCK là tứ giác nội tiếp đường tròn đường kính KB

=>BHCK nội tiếp (T)

=>TB=TH=TC=TK

Vì \(sđ\stackrel\frown{AC}=60^0\)

nên \(\widehat{ABC}=30^0\)

=>\(\widehat{CBH}=30^0\)

Xét (T) có \(\widehat{CBH}\) là góc nội tiếp chắn cung CH

nên \(\widehat{CTH}=2\cdot\widehat{CBH}=60^0\)

Xét ΔTCH cân tại T có \(\widehat{CTH}=60^0\)

nên ΔTCH đều

Lời giải:

Vì $AD, BE, CF$ là đường cao của tam giác $ABC$ và cắt nhau tại $H$ nên $\widehat{HFA}=\widehat{HEA}=90^0$

Tứ giác $AEHF$ có tổng hai góc đối nhau $\widehat{AEH}+\widehat{AFH}=90^0+90^0=180^0$ nên $AEHF$ là tứ giác nội tiếp.

------------------

Kẻ tiếp tuyến $Ax$ của $(O)$. Ta có $OA\perp Ax(1)$

$\widehat{xAB}=\widehat{ACB}=\widehat{ECB}(2)$ (góc tạo bởi tiếp tuyến và dây cung bằng góc nt chắn cung đó - cung $AB$)

Tứ giác $BFEC$ có $\widehat{BFC}=\widehat{BEC}=90^0$ và cùng nhìn cạnh $BC$ nên $BFEC$ là tứ giác nội tiếp.

$\Rightarrow \widehat{ECB}=\widehat{AFE}(3)$

Từ $(2); (3)\Rightarrow \widehat{xAB}=\widehat{AFE}$

Mà 2 góc này ở vị trí so le trong nên $Ax\parallel EF(4)$

Từ $(1); (4)\Rightarrow OA\perp EF$

Hình vẽ:

a: Xét tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=90^0+90^0=180^0\)

nên AEHF là tứ giác nội tiếp

Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}=90^0\)

nên BFEC là tứ giác nội tiếp

=>\(\widehat{FEC}+\widehat{FBC}=180^0\)

mà \(\widehat{FEC}+\widehat{AEF}=180^0\)(hai góc kề bù)

nên \(\widehat{AEF}=\widehat{ABC}\)

Kẻ tiếp tuyến Ax của (O) tại A

=>OA\(\perp\)Ax tại A

Xét (O) có

\(\widehat{xAC}\) là góc tạo bởi tiếp tuyến Ax và dây cung AC

\(\widehat{ABC}\) là góc nội tiếp chắn cung AC

Do đó: \(\widehat{xAC}=\widehat{ABC}\)

=>\(\widehat{xAC}=\widehat{AEF}\)

mà hai góc này là hai góc ở vị trí so le trong

nên EF//Ax

=>EF\(\perp\)OA

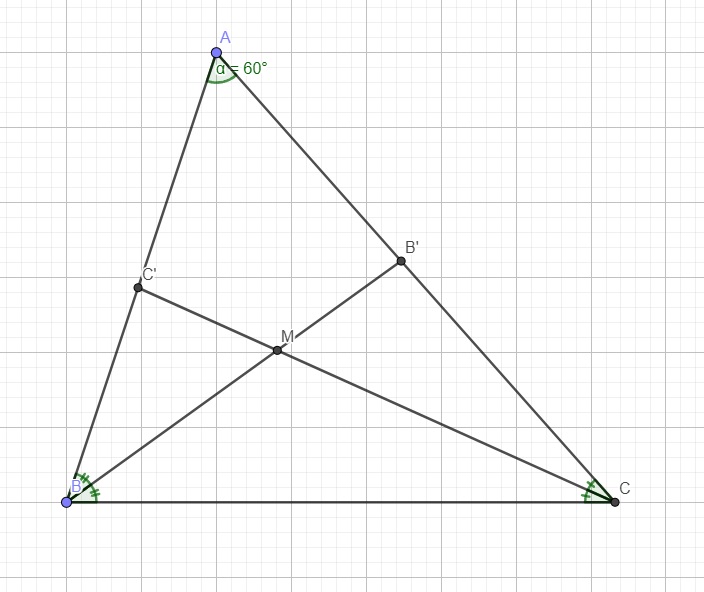
Ta có \(\widehat{B}+\widehat{C}=180^0-\widehat{A}=120^0\)

\(\Rightarrow\widehat{MBC}+\widehat{MCB}=\dfrac{1}{2}\widehat{B}+\dfrac{1}{2}\widehat{C}=60^0\)

\(\Rightarrow\widehat{BMC}=180^0-\left(\widehat{MBC}+\widehat{MCB}\right)=120^0\)

\(\Rightarrow\widehat{B'MC'}=\widehat{BMC}=120^0\) (đối đỉnh)

\(\Rightarrow\widehat{A}+\widehat{B'MC'}=60^0+120^0=180^0\)

\(\Rightarrow AB'MC'\) nội tiếp

\(ac=-12< 0\) nên pt luôn có 2 nghiệm pb trái dấu với mọi m

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m-1\\x_1x_2=-12\end{matrix}\right.\)

\(\left(x_1-1\right)\left(x_2-1\right)+12=0\)

\(\Leftrightarrow x_1x_2-x_1-x_1+1+12=0\)

\(\Leftrightarrow x_1x_2-\left(x_1+x_2\right)+13=0\)

\(\Leftrightarrow-12-\left(m-1\right)+13=0\)

\(\Leftrightarrow2-m=0\)

\(\Leftrightarrow m=2\)

Lời giải:

a. Xét tam giác $ABC$ và $HBA$ có:

$\widehat{BAC}=\widehat{BHA}=90^0$

$\widehat{B}$ chung

$\Rightarrow \triangle ABC\sim \triangle HBA$ (g.g)

$\Rightarrow \frac{AB}{HB}=\frac{BC}{BA}$

$\Rightarrow AB^2=HB.BC$

b.

$BC=BH+CH=4+9=13$ (cm) 

Từ kết quả phần b:

$AB^2=BH.BC=4.13=52\Rightarrow AB=\sqrt{52}$ (cm) 

$AH=\sqrt{AB^2-BH^2}=\sqrt{52-4^2}=6$ (cm) - áp dụng định lý Pitago

c.

Xét tam giác $AFH$ và $CEH$ có:

$\widehat{FHA}=\widehat{EHC}$ (cùng phụ $\widehat{AHE}$)

$\widehat{FAH}=\widehat{ECH}$ (cùng phụ $\widehat{HAC}$)

$\Rightarrow \triangle AFH\sim \triangle CEH$ (g.g)

Hình vẽ: