Bài 1: Tính B = 1 + 2 + 3 +...+ 98 + 99
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Dấu âm đó là dấu âm của tử thôi bạn. Và vì mẫu số phải đáp ứng điều kiện là `<0` để là một phân số, nên nếu mẫu số có dấu âm sẽ được chuyển lên tử nhé! Nếu cả 2 đều chứa dấu âm thì phân số đó dương.
Ta có công thức luỹ thừa của một số hữu tỉ như sau:
(\(\dfrac{a}{b}\))m = \(\dfrac{a^m}{b^m}\) (a; b; m \(\in\) Z; b ≠ 0)
Áp dụng với ( \(\dfrac{-1}{2}\) )7 ta có a = -1; b = 2; m = 7
Khi đó: (\(\dfrac{-1}{2}\))7 = \(\dfrac{\left(-1\right)^7}{\left(2\right)^7}\) = \(\dfrac{-1}{128}\)

1:
a: \(\dfrac{1234}{1244}=1-\dfrac{10}{1244}\)
\(\dfrac{4321}{4331}=1-\dfrac{10}{4331}\)
1244<4331
=>\(\dfrac{10}{1244}>\dfrac{10}{4331}\)
=>\(-\dfrac{10}{1244}< -\dfrac{10}{4331}\)
=>\(-\dfrac{10}{1244}+1< -\dfrac{10}{4331}+1\)
=>\(\dfrac{1234}{1244}< \dfrac{4321}{4331}\)
=>\(-\dfrac{1234}{1244}>-\dfrac{4321}{4331}\)
2:
a: \(\dfrac{33}{131}>\dfrac{33}{132}=\dfrac{1}{4}\)
\(\dfrac{53}{217}< \dfrac{53}{212}=\dfrac{1}{4}\)
Do đó: \(\dfrac{33}{131}>\dfrac{53}{217}\)
=>\(-\dfrac{33}{131}< -\dfrac{53}{217}\)
b: \(\dfrac{22}{67}< \dfrac{22}{66}=\dfrac{1}{3}\)
\(\dfrac{51}{152}>\dfrac{51}{153}=\dfrac{1}{3}\)
Do đó: \(\dfrac{22}{67}< \dfrac{51}{152}\)
=>\(\dfrac{22}{-67}>\dfrac{51}{-152}\)
c: \(\dfrac{18}{91}< \dfrac{18}{90}=\dfrac{1}{5}\)
\(\dfrac{23}{114}>\dfrac{23}{115}=\dfrac{1}{5}\)
Do đó: \(\dfrac{18}{91}< \dfrac{23}{114}\)
=>\(-\dfrac{18}{91}>-\dfrac{23}{114}\)

Bài 4:
\(\left(x-\dfrac{2}{5}\right)^2>=0\forall x\)
\(\left(y+20\right)^{10}>=0\forall y\)
Do đó: \(\left(x-\dfrac{2}{5}\right)^2+\left(y+20\right)^{10}>=0\forall x,y\)
=>\(A=\left(x-\dfrac{2}{5}\right)^2+\left(y+20\right)^{10}+2010>=2010\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-\dfrac{2}{5}=0\\y+20=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{2}{5}\\y=-20\end{matrix}\right.\)
Bài 3:
\(\left(ad+bc\right)^2=4bacd\)
=>\(a^2d^2+b^2c^2+2adbc-4adbc=0\)
=>\(\left(ad\right)^2+\left(bc\right)^2-2adbc=0\)
=>(ad-bc)2=0
=>ad-bc=0
=>ad=bc
=>\(\dfrac{a}{b}=\dfrac{c}{d}\)
=>ĐPCM
Bài 2:
a: |2x-1|+3=15
=>|2x-1|=15-3=12
=>\(\left[{}\begin{matrix}2x-1=12\\2x-1=-12\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{13}{2}\\x=-\dfrac{11}{2}\end{matrix}\right.\)
b: \(\left|x-3,2\right|+\left|2x-\dfrac{1}{5}\right|=x+3\)(1)
TH1: x<1/10
(1) sẽ trở thành \(\dfrac{1}{5}-2x+3,2-x=x+3\)
=>-3x+3,4=x+3
=>-4x=3-3,4=-0,4
=>x=0,1(loại)
TH2: 1/10<=x<3,2
(1) sẽ trở thành \(2x-\dfrac{1}{5}+3,2-x=x+3\)
=>x+3=x+3(luôn đúng)
TH3: x>=3,2
(1) sẽ trở thành \(x-3,2+2x-\dfrac{1}{5}=x+3\)
=>3x-3,4=x+3
=>2x=6,4
=>x=3,2(nhận)
Vậy: 1/10<=x<=3,2

Ta có:$\frac23< a-\frac16<\frac89$
$\Rightarrow \frac23+\frac16< a-\frac16+\frac16<\frac89+\frac16$
$\Rightarrow \frac56< a<\frac{19}{18}$
Mà a nguyên nên $a=1$

Khi x=-99 và y=99 thì \(x^4-y^4=\left(-99\right)^4-99^4=99^4-99^4=0\)


Số tiền phải trả khi mua 1 chiếc máy tính là:
\(700000\cdot\left(100\%-10\%\right)=630000\) (đồng)
Số tiền phải trả khi mua 7 cái bút là:
\(7\cdot10000\cdot\left(100\%-5\%\right)=66500\) (đồng)
Số tiền phải trả khi mua x quyển vở là:
\(x\cdot20000\cdot\left(100\%-20\%\right)=x\cdot20000\cdot80\%=16000x\) (đồng)
Biểu thức đại số thể hiện tổng số tiền phải trả là:
\(630000+66500+16000x=696500+16000x\)
máy tính sau khi giảm giá là:
700000 x (1 - 10%) = 630000 (đồng)
quyển vở sau khi giảm giá là:
20000 x (1 - 20%) = 16000 (đòng)
chiếc bút sau khi giảm giá là:
10000 x (1 - 5%) = 9,500 (đồng)
số tiền mua 1 chiếc máy tính là: 630000 đồng
số tiền mua 7 chiếc bút là: 7 x 9500 = 66500 đồng
số tiền mua x quyển vở là: 16000x đồng
BIỂU THỨC ĐẠI SỐ TỔNG SỐ TIỀN LÀ:
630000 + 66500 + 1600x
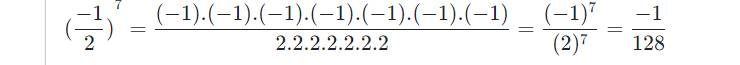


`#3107.101107`
`1.`
Số hạng của tổng B:
`(99 - 1) \div 1 + 1 = 99` (số hạng)
Giá trị của tổng B:
`(99 + 1) \cdot 99 \div 2 = 4950`