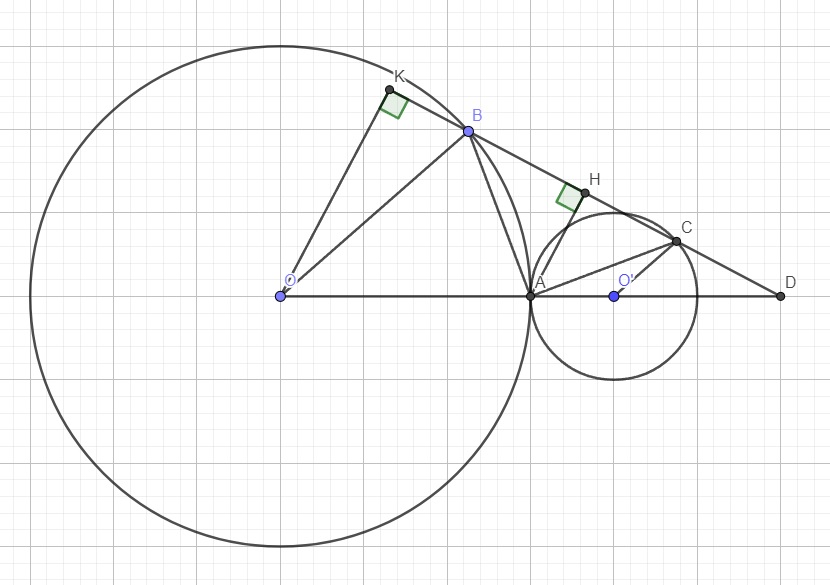
Đường tròn tâm O,MA là tiếp tuyết đường tròn tâm O tại A.
MBC là cát tuyến,dây AD vuông góc với MO ở H.
a,CM MD là tiếp tuyến
b,cm tam giác MHB đồng dạng tam giác MCO
C,gọi I là trung điểm bc
Cm đường tròn ngoại tiếp tam giác MAD đi qua I
D,GIAO OI và AD là Q
cm QB,QC LÀ TIẾP TUYẾN ĐƯỜNG TRÒN TÂM O


 Tại sao em trả lời trong thời gian trên mà không được COIN ạ ?
Tại sao em trả lời trong thời gian trên mà không được COIN ạ ?

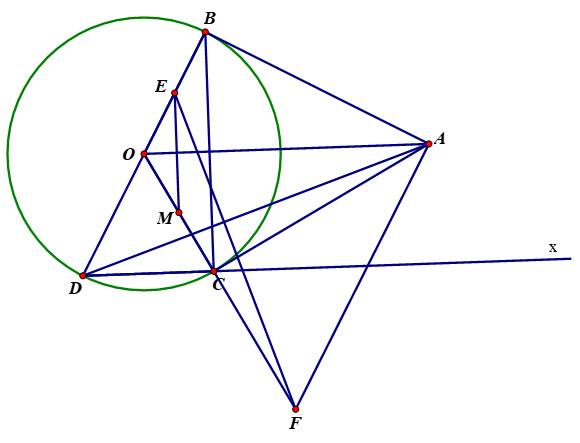
Trình bày ngắn gọn hướng giải, chi tiết tỉ mỉ em tự thực hiện
a.
AD vuông góc MO tại H \(\Rightarrow HA=HD\)
\(\Rightarrow\Delta_{\perp}OHA=\Delta_{\perp}OHD\left(c.g.c\right)\)
\(\Rightarrow\widehat{HOA}=\widehat{HOD}\)
\(\Rightarrow\Delta MOA=\Delta MOD\left(c.g.c\right)\)
\(\Rightarrow\widehat{MDO}=\widehat{MAO}=90^0\)
\(\Rightarrow MD\) là tiếp tuyến
b.
\(\widehat{MAB}=\widehat{MCA}\) (góc nt và góc tạo bởi tiếp tuyến - dây cung cùng chắn AB)
\(\Rightarrow\Delta MAB\sim\Delta MCA\)
\(\Rightarrow\dfrac{MA}{MC}=\dfrac{MB}{MA}\Rightarrow MA^2=MB.MC\)
Hệ thức lượng trong tam giác vuông MAO với đường cao AH:
\(MA^2=MH.MO\)
\(\Rightarrow MB.MC=MH.MO\Rightarrow\dfrac{MB}{MO}=\dfrac{MH}{MC}\)
Lại có \(\widehat{HMB}\) chung
\(\Rightarrow\Delta MHB\sim\Delta MCO\left(c.g.c\right)\)
c.
MA, MD là tiếp tuyến nên các tam giác MAO, MDO vuông
\(\Rightarrow M,A,D,O\) thuộc đường tròn đường kính MO
I là trung điểm BC \(\Rightarrow OI\perp BC\)
\(\Rightarrow\Delta MOI\) vuông tại I nên M, O, I thuộc đường tròn đường kính MO
\(\Rightarrow I,A,M,D\) cùng thuộc đường tròn đường kính MO
Hay đường tròn ngoại tiếp MAD đi qua I
d.
Kẻ tiếp tuyến tại B và C của (O) cắt nhau tại P
\(\Rightarrow\) Các tam giác PBO và PCO vuông nên P, B, C, O thuộc đường tròn đường kính OP (1)
Mặt khác OI đi qua trung điểm BC \(\Rightarrow OI\) là trung trực BC
\(PB=PC\) (hai tiếp tuyến cắt nhau), \(OB=OC=R\) nên OP là trung trực BC
\(\Rightarrow P,O,I\) thẳng hàng hay P nằm trên OI (2)
Từ câu b ta có \(\Delta MHB\sim\Delta MCO\Rightarrow\widehat{MCO}=\widehat{MHB}\)
Mà \(\widehat{MHB}+\widehat{BHO}=180^0\Rightarrow\widehat{MCO}+\widehat{BHO}=180^0\)
\(\Rightarrow BCOH\) nội tiếp hay 4 điểm B, C, O, H cùng thuộc 1 đường tròn (3)
(1);(3) \(\Rightarrow P,C,O,B,H\) cùng thuộc đường tròn đường kính PO
\(\Rightarrow\widehat{PHO}\) là góc nt chắn nửa đường tròn (do PO là đường kính)
\(\Rightarrow PH\perp OM\)
Mà \(AD\perp OM\) hay \(AH\perp OM\) theo giả thiết
\(\Rightarrow\) Đường thẳng PH trùng đường thẳng AD, hay P nằm trên đường thẳng AD (4)
(2);(4) \(\Rightarrow P\) là giao điểm của OI và AD
\(\Rightarrow P\) trùng Q
\(\Rightarrow Q\) là giao điểm 2 tiếp tuyến tại B và C
Hay QB, QC là tiếp tuyến của (O)