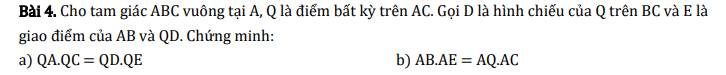
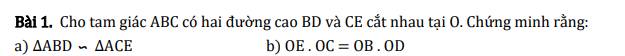
bài 1:

Gọi thời gian dự định hoàn thành công việc là x(ngày)

(Điều kiện: x>0)

Thời gian thực tế hoàn thành công việc là x-2(ngày)

Trong 1 ngày dự kiến làm được \(\dfrac{120}{x}\left(cái\right)\)

Trong 1 ngày thực tế làm được \(\dfrac{120}{x-2}\left(áo\right)\)

Mỗi ngày làm được nhiều hơn 3 cái so với dự kiến nên ta có phương trình:

\(\dfrac{120}{x-2}-\dfrac{120}{x}=3\)

=>\(\dfrac{40}{x-2}-\dfrac{40}{x}=1\)

=>\(\dfrac{40x-40x+80}{x\left(x-2\right)}=1\)

=>\(\dfrac{80}{x\left(x-2\right)}=1\)

=>x(x-2)=80

=>\(x^2-2x-80=0\)

=>(x-10)(x+8)=0

=>\(\left[{}\begin{matrix}x=10\left(nhận\right)\\x=-8\left(loại\right)\end{matrix}\right.\)

Vậy: thời gian dự định hoàn thành công việc là 10 ngày

a: Xét ΔAMH vuông tại M và ΔAHB vuông tại H có

\(\widehat{MAH}\) chung

Do đó: ΔAMH~ΔAHB

=>\(\dfrac{AM}{AH}=\dfrac{AH}{AB}\)

=>\(AH^2=AM\cdot AB\left(1\right)\)

b: Xét ΔANH vuông tại N và ΔAHC vuông tại H có

\(\widehat{NAH}\) chung

Do đó: ΔANH~ΔAHC

=>\(\dfrac{AN}{AH}=\dfrac{AH}{AC}\)

=>\(AH^2=AN\cdot AC\left(2\right)\)

Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)

c: ta có: \(AM\cdot AB=AN\cdot AC\)

=>\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)

Xét ΔAMN vuông tại A và ΔACB vuông tại A có

\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)

Do đó: ΔAMN~ΔACB

d: Ta có: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC^2=9^2+12^2=15^2\)

=>BC=15(cm)

Xét ΔABC vuông tại A có AH là đường cao

nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot AB\cdot AC\)

=>\(AH\cdot BC=AB\cdot AC\)

=>\(AH\cdot15=9\cdot12=108\)

=>AH=108:15=7,2(cm)

Xét tứ giác AMHN có \(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)

nên AMHN là hình chữ nhật

=>AH=MN=7,2(cm)

ΔABC vuông tại A

=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot9\cdot12=54\left(cm^2\right)\)

Ta có: ΔAMN~ΔACB

=>\(\dfrac{S_{AMN}}{S_{ACB}}=\left(\dfrac{MN}{CB}\right)^2\)

=>\(\dfrac{S_{AMN}}{54}=\left(\dfrac{7.2}{15}\right)^2\)

=>\(S_{AMN}=12,4416\left(cm^2\right)\)

a: Xét ΔBIH vuông tại I và ΔBDC vuông tại D có

\(\widehat{IBH}\) chung

Do đó: ΔBIH~ΔBDC

b: Ta có: ΔBIH~ΔBDC

=>\(\dfrac{BI}{BD}=\dfrac{BH}{BC}\)

=>\(BH\cdot BD=BI\cdot BC\)

Xét ΔCIH vuông tại I và ΔCEB vuông tại E có

\(\widehat{ECB}\) chung

Do đó: ΔCIH~ΔCEB

=>\(\dfrac{CI}{CE}=\dfrac{CH}{CB}\)

=>\(CH\cdot CE=CI\cdot CB\)

\(BH\cdot BD+CH\cdot CE\)

\(=BI\cdot BC+CI\cdot BC\)

\(=BC\left(BI+CI\right)=BC^2\)

a: Xét ΔQDC vuông tại D và ΔQAE vuông tại A có

\(\widehat{DQC}=\widehat{AQE}\)(hai góc đối đỉnh)

Do đó: ΔQDC~ΔQAE

=>\(\dfrac{QD}{QA}=\dfrac{QC}{QE}\)

=>\(QD\cdot QE=QC\cdot QA\)

b: Xét ΔAEQ vuông tại A và ΔACB vuông tại A có

\(\widehat{AEQ}=\widehat{ACB}\left(=90^0-\widehat{DBA}\right)\)

Do đó: ΔAEQ~ΔACB

=>\(\dfrac{AE}{AC}=\dfrac{AQ}{AB}\)

=>\(AE\cdot AB=AQ\cdot AC\)

a: Xét ΔFHD vuông tại H và ΔFDE vuông tại D có

\(\widehat{HFD}\) chung

Do đó: ΔFHD~ΔFDE

b: Ta có: ΔFHD~ΔFDE

=>\(\dfrac{FH}{FD}=\dfrac{FD}{FE}\)

=>\(FD^2=FH\cdot FE\)

c: \(FD^2=FH\cdot FE=5,4\cdot15=81\)

=>\(FD=\sqrt{81}=9\left(cm\right)\)

Ta có: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(AB^2=6^2-4^2=20\)

=>\(AB=2\sqrt{5}\left(cm\right)\)

Ta có: ΔDCB vuông tại C

=>\(CB^2+CD^2=DB^2\)

=>\(CD^2=9^2-6^2=81-36=45\)

=>\(CD=3\sqrt{5}\left(cm\right)\)

Xét ΔBAC vuông tại A và ΔDCB vuông tại C có

\(\dfrac{BA}{DC}=\dfrac{AC}{CB}\left(\dfrac{2\sqrt{5}}{3\sqrt{5}}=\dfrac{4}{6}=\dfrac{2}{3}\right)\)

Do đó: ΔBAC~ΔDCB

=>\(\widehat{BCA}=\widehat{DBC}\)

mà hai góc này là hai góc ở vị trí so le trong

nên BD//AC

a: Xét ΔABD vuông tại D và ΔACE vuông tại E có

\(\widehat{BAD}\) chung

Do đó: ΔABD~ΔACE

b: Xét ΔOEB vuông tại E và ΔODC vuông tại D có

\(\widehat{EOB}=\widehat{DOC}\)(hai góc đối đỉnh)

Do đó: ΔOEB~ΔODC

=>\(\dfrac{OE}{OD}=\dfrac{OB}{OC}\)

=>\(OE\cdot OC=OD\cdot OB\)

  Olm chào em, đây là dạng toán nâng cao giải phương trình nghiệm nguyên. cấu trúc thi chuyên. Hôm nay olm.vn sẽ hướng dẫn em giải dạng này bằng phương pháp chặn kết hợp với lập bảng chi tiết như sau:

       Bước 1:  Chặn để giới hạn nghiệm cần tìm trong một khoảng nào đó.

       Bước 2: Kết hợp với điều kiện lập bảng tìm nghiệm nguyên

        Bước 3 kết luận: 

                         Giải:

              \(x^2\) + y² + 2\(x\) = 17

              \(x^2\) + y² +  2\(x\) + 1 = 17 + 1

            (\(x^2\) + 2\(x\) + 1) + y² = 18

              (\(x\) + 1)² + y² = 18

Vì y² ≥ 0 ∀ y nên 0 ≤ y² ≤ 18

 Vì y \(\in\) Z  nên y² \(\in\) {0; 1; 4; 9; 16; 25; ...;}

Vì 0 ≤ y² ≤ 18 nên y² \(\in\) {0; 1; 4; 9; 16}

Lập bảng ta có:

Theo bảng trên ta có các cặp \(x;y\) nguyên thỏa mãn đề bài là:

(\(x;y\)) = (-4; -3); (-4; 3); (2; -3); (2; 3)

Vậy (\(x;y\)) = (-4; -3); (-4; 3); (2; -3); (2; 3) là nghiệm nguyên của phương trình.

A B C D E F I M

b/

\(C_{MCE}=MC+ME+CE\)

Mà ME=MF (cmt)

\(\Rightarrow C_{MCE}=MC+MF+CE=MC+MD+DF+CE=\) 

\(=CD+DF+CE\) Mà DF=BE (gt)

\(\Rightarrow C_{MCE}=CD++BE+CE=CD+BC=2.BC\) không đổi

a: Ta có; ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC^2=3^2+4^2=25=5^2\)

=>BC=5
Xét ΔBAC có BD là phân giác

nên \(\dfrac{AD}{DC}=\dfrac{BA}{BC}=\dfrac{3}{5}\)(1)

b: Ta có: AH\(\perp\)BC

DE\(\perp\)BC

Do đó: AH//DE

Xét ΔCAH có DE//AH

nên \(\dfrac{HE}{EC}=\dfrac{AD}{DC}\)(2)

Từ (1),(2) suy ra \(\dfrac{HE}{EC}=\dfrac{BA}{BC}\)

giúp mik vs