Ta có : \(P=\sqrt{2x^2+xy+2y^2}+\sqrt{2y^2+yz+2z^2}+\sqrt{2z^2+xz+2x^2}\)

Xét : \(\sqrt{2x^2+xy+2y^2}=\sqrt{\dfrac{3}{4}.\left(x-y\right)^2+\dfrac{5}{4}.\left(x+y\right)^2}\)

\(\ge\sqrt{\dfrac{5}{4}.\left(x+y\right)^2}=\dfrac{\sqrt{5}}{2}.\left(x+y\right)\)

\(CMTT:\sqrt{2y^2+yz+2z^2}\ge\dfrac{\sqrt{5}}{2}.\left(y+z\right)\)

                \(\sqrt{2z^2+xz+2x^2}\ge\dfrac{\sqrt{5}}{2}.\left(x+z\right)\)

Do đó : \(P\ge\dfrac{\sqrt{5}}{2}.\left(x+y+y+z+z+x\right)=\dfrac{2\sqrt{5}.\left(x+y+z\right)}{2}\)

\(\Rightarrow P\ge\sqrt{5}.\left(x+y+z\right)\)

Ta có : BĐT : \(\left(a+b+c\right)^2\ge3\left(ab+bc+ca\right)\)

\(\Rightarrow\left(x+y+z\right)^2\ge3\left(xy+yz+zx\right)\)

Mà : \(xy+yz+zx=3\)

\(\Rightarrow\left(x+y+z\right)^2\ge9\)

\(\Leftrightarrow x+y+z\ge3\)

\(\Rightarrow P_{min}=3\sqrt{5}\)

Dấu bằng xảy ra : \(\Leftrightarrow x=y=z=1\)

\(\sqrt{x-2}+\sqrt{6-x}\text{=}\sqrt{x^2-8x+24}\)

\(ĐKXĐ:2\le x\le6\)

Xét VP của pt ta thấy : \(\sqrt{x^2-8x+24}\text{=}\sqrt{x^2-8x+16+8}\)

\(\text{=}\sqrt{\left(x-4\right)^2+8}\)

\(\Rightarrow VP\ge\sqrt{8}\)

Xét VT của pt ta có :

\(VT^2\text{=}x-2+6-x+2\sqrt{\left(x-2\right)\left(6-x\right)}\)

\(VT^2\text{=}4+2\sqrt{\left(x-2\right)\left(6-x\right)}\)

Áp dụng BĐT cô si cho 2 số không âm ta có :

\(2\sqrt{\left(x-2\right)\left(6-x\right)}\le\left(\sqrt{x-2}\right)^2+\left(\sqrt{6-x}\right)^2\)

\(\text{=}x-2+6-x\text{=}4\)

\(\Rightarrow VT^2\le8\)

\(\Rightarrow VT\le\sqrt{8}\)

Để \(VT\text{=}VP\) \(\Leftrightarrow\left\{{}\begin{matrix}x-4\text{=}0\\\sqrt{x-2}\text{=}\sqrt{6-x}\end{matrix}\right.\)

\(\Leftrightarrow x=4\left(TM\right)\)

Vậy...........

d3//d1 => a=2 (b khác 1)

d3 cắt d2 tại điểm có tung độ bằng 2 Thay y=2 vào d2

=> 2=-x+4=> x=2 Thay y=2; x=2; a=2 vào d3

=> 2+2.2+b=> b=-6

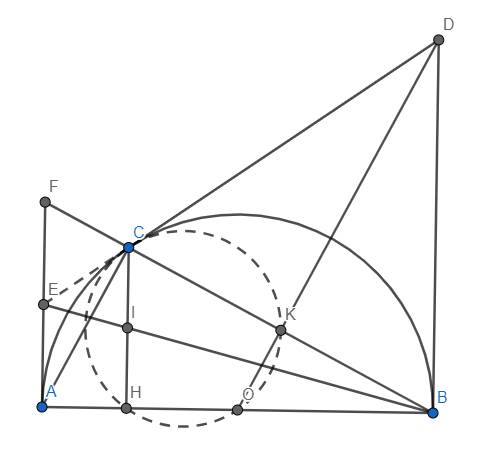
a) Ta thấy OK là đường trung bình của tam giác ABC \(\Rightarrow\) OK//AC.

Mà \(AC\perp CB\) tại C nên \(OK\perp BC\) tại K hay \(DK\perp BC\) tại K

 Tam giác BCD có DK vừa là đường cao, vừa là trung tuyến nên tam giác BCD cân tại D, suy ra \(DB=DC\) (đpcm)

 Dễ dàng chứng minh \(\Delta OBD=\Delta OCD\left(c.c.c\right)\) \(\Rightarrow\widehat{OCD}=\widehat{OBD}=90^o\), suy ra DC tiếp xúc với (O) tại C. (đpcm)

 b) Tứ giác OHCK có \(\widehat{CHO}+\widehat{CKO}=90^o+90^o=180^o\) nên OHCK nội tiếp, điều này có nghĩa là \(C\in\left(OHK\right)\) (đpcm)

 c) Gọi F là giao điểm của BC và AE. Do CH//AF nên theo bổ đề hình thang, E là trung điểm của AF.

 Tam giác CAF vuông tại C có trung tuyến CE nên \(CE=\dfrac{1}{2}AF=EA\), suy ra tam giác ACE cân tại E 

 \(\Rightarrow\widehat{ECA}=\widehat{EAC}\)

Mặt khác, EA tiếp xúc với (O) tại A nên \(\widehat{EAC}=\dfrac{1}{2}sđ\stackrel\frown{AC}\)

Từ đó suy ra \(\widehat{EAC}=\dfrac{1}{2}sđ\stackrel\frown{AC}\) \(\Rightarrow\) EC tiếp xúc với (O) tại C.

Mà DC cũng tiếp xúc với (O) tại C nên D, E, C thẳng hàng (đpcm)

Bài 4:

Ta có \(\dfrac{1}{a^2\left(b+c\right)}=\dfrac{abc}{a^2\left(b+c\right)}=\dfrac{bc}{ab+ca}\)

Tương tự: \(\dfrac{1}{b^2\left(c+a\right)}=\dfrac{ca}{bc+ab}\) và \(\dfrac{1}{c^2\left(a+b\right)}=\dfrac{ab}{bc+ca}\)

Đặt \(\left\{{}\begin{matrix}bc=x\\ca=y\\ab=z\end{matrix}\right.\) với \(x,y,z>0;xyz=1\)

Khi đó BĐT cần chứng minh trở thành:

 \(\dfrac{x}{y+z}+\dfrac{y}{z+x}+\dfrac{z}{x+y}\ge\dfrac{3}{2}\) 

Thật vậy, đặt \(P=\dfrac{x}{y+z}+\dfrac{y}{z+x}+\dfrac{z}{x+y}\)

\(P=\dfrac{x^2}{xy+zx}+\dfrac{y^2}{yz+xy}+\dfrac{z^2}{zx+yz}\)

\(P\ge\dfrac{\left(x+y+z\right)^2}{2\left(xy+yz+zx\right)}\) (BĐT B.C.S)

Mà lại có \(xy+yz+zx\le\dfrac{\left(x+y+z\right)^2}{3}\) nên ta có:

\(P\ge\dfrac{\left(x+y+z\right)^2}{2.\dfrac{\left(x+y+z\right)^2}{3}}=\dfrac{3}{2}\) Vậy ta có đpcm. 

Dấu "=" xảy ra \(\Leftrightarrow x=y=z=1\) \(\Leftrightarrow a=b=c=1\)

Ta có \(\sqrt{x+2}-y^3=\sqrt{y+2}-x^3\)

\(\Leftrightarrow\sqrt{x+2}+x^3=\sqrt{y+2}+y^3\)

 Đặt \(f\left(x\right)=\sqrt{x+2}+x^3\). Ta chứng minh \(f\left(x\right)\) là hàm số đồng biến với \(x\ge-2\)

Giả sử \(f\left(a\right)>f\left(b\right)\) với \(a,b\ge-2\)

\(\Rightarrow\sqrt{a+2}+a^3>\sqrt{b+2}+b^3\)

\(\Leftrightarrow\sqrt{a+2}-\sqrt{b+2}+a^3-b^3>0\)

\(\Leftrightarrow\dfrac{a-b}{\sqrt{a+2}+\sqrt{b+2}}+\left(a-b\right)\left(a^2+ab+b^2\right)>0\)

\(\Leftrightarrow\left(a-b\right)\left(\dfrac{1}{\sqrt{a+2}+\sqrt{b+2}}+a^2-ab+b^2\right)>0\)     (*)

 Dễ thấy \(\dfrac{1}{\sqrt{a+2}+\sqrt{b+2}}+a^2+ab+b^2>0\) với mọi \(a,b\ge-2\)

 Do đó từ (*) suy ra \(a>b\).

 Vậy ta có \(f\left(a\right)>f\left(b\right)\Rightarrow a>b\). Do đó \(f\) là hàm số đồng biến.

 Theo trên, ta có \(f\left(x\right)=f\left(y\right)\Rightarrow x=y\)

 Thay vào biểu thức B, ta có \(B=x^2+2x+10\)

\(B=\left(x+1\right)^2+9\) \(\ge9\).

 Dấu "=" xảy ra \(\Leftrightarrow x=-1\) (nhận) \(\Rightarrow y=-1\)

 Vậy GTNN của B là 9, xảy ra khi \(\left(x;y\right)=\left(-1;-1\right)\)

yêu cầu ?

= 2 căn 6 - 3 + 3 - căn 6

= căn 6

Cho mình xin 1 tick nha trang

\(sina=\dfrac{12}{13}\\ \Rightarrow cosa=\sqrt{1-\left(\dfrac{12}{13}\right)^2}=\dfrac{5}{13}\\ tana=\dfrac{sina}{cosa}=\dfrac{\dfrac{12}{13}}{\dfrac{5}{13}}=\dfrac{12}{5}\)

\(2\sqrt{5}-\sqrt{125}+\sqrt{80}+\sqrt{605}\)

\(=2\sqrt{5}-5\sqrt{5}+4\sqrt{5}+11\sqrt{5}\)

\(=\left(2-5+4+11\right)\sqrt{5}\)

\(=12\sqrt{5}\)