Lời giải:
Áp dụng TCDTSBN:

$\frac{1}{x+y+z}=\frac{y+z+1}{x}=\frac{x+z+2}{y}=\frac{x+y-3}{z}=\frac{y+z+1+x+z+2+x+y-3}{x+y+z}=\frac{2(x+y+z)}{x+y+z}=2$

\(\Rightarrow \left\{\begin{matrix} x+y+z=\frac{1}{2}\\ y+z+1=2x\\ x+z+2=2y\\ x+y-3=2z\end{matrix}\right.\Rightarrow \left\{\begin{matrix} x+y+z=\frac{1}{2}\\ x+y+z+1=3x\\ x+y+z+2=3y\\ x+y+z-3=3z\end{matrix}\right.\)

\(\left\{\begin{matrix} \frac{1}{2}+1=3x\\ \frac{1}{2}+2=3y\\ \frac{1}{2}-3=3z\end{matrix}\right.\Rightarrow \left\{\begin{matrix} x=\frac{1}{2}\\ y=\frac{5}{6}\\ z=\frac{-5}{6}\end{matrix}\right.\)

Ta có: \(\dfrac{x}{3}=\dfrac{y}{4}\Rightarrow\dfrac{x}{15}=\dfrac{y}{20}\)

\(\dfrac{y}{5}=\dfrac{z}{7}\Rightarrow\dfrac{y}{20}=\dfrac{z}{28}\)

\(\Rightarrow\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{y}{28}=\dfrac{2x+3y-z}{15\cdot2+3\cdot20-28}=\dfrac{186}{62}=3\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{15}=3\Rightarrow x=45\\\dfrac{y}{20}=3\Rightarrow y=60\\\dfrac{z}{28}=3\Rightarrow z=84\end{matrix}\right.\)

Vậy: ... 

�3=�4;�5=�7⇒�15=�20;�20=�283x​=4y​;5y​=7z​⇒15x​=20y​;20y​=28z​

Áp dụng tính chất dãy tỉ số bằng nhau :

�15=�20=�28=2�+3�−�30+60−28=18662=315x​=20y​=28z​=30+60−282x+3y−z​=62186​=3

⇒�15=3.15=45⇒15x​=3.15=45

⇒�20=3.20=60⇒20y​=3.20=60

⇒�28=3.28=84⇒28z​=3.28=84

Vậy x = 45; y= 60; z = 84

a) Xét hai tam giác vuông: ∆AHB và ∆DHB có:

AH = DH (gt)

BH là cạnh chung

⇒ ∆AHB = ∆DHB (hai cạnh góc vuông)

b) Xét hai tam giác vuông: ∆AHC và ∆DHC có:

AH = DH (gt)

CH là cạnh chung

⇒ ∆AHC = ∆DHC (hai cạnh góc vuông)

c) Do ∆AHB = ∆DHB (cmt)

⇒ AB = DB (hai cạnh tương ứng)

Do ∆AHC = ∆DHC (cmt)

⇒ AC = DC (hai cạnh tương ứng)

Xét ∆ABC và ∆DBC có:

BC là cạnh chung

AB = DB (cmt)

AC = DC (cmt)

⇒ ∆ABC = ∆DBC (c-c-c)

Ta có:

\(\dfrac{1}{2^2}=\dfrac{1}{2\cdot2}< \dfrac{1}{1\cdot2}\)

\(\dfrac{1}{3^2}=\dfrac{1}{3\cdot3}< \dfrac{1}{2\cdot3}\)

\(\dfrac{1}{4^2}=\dfrac{1}{4\cdot4}< \dfrac{1}{3\cdot4}\)

...

\(\dfrac{1}{9^2}=\dfrac{1}{9\cdot9}< \dfrac{1}{8\cdot9}\)

\(\dfrac{1}{10^2}=\dfrac{1}{10\cdot10}< \dfrac{1}{9\cdot10}\)

\(\Rightarrow A=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{10^2}< \dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{9\cdot10}\)

\(\Rightarrow A< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}\)

\(\Rightarrow A< 1-\dfrac{1}{10}\)

\(\Rightarrow A< \dfrac{9}{10}\)

\(\Rightarrow A< 1\) (vì: \(\dfrac{9}{10}< 1\))

221​=2⋅21​<1⋅21​

132=13⋅3<12⋅3321​=3⋅31​<2⋅31​

142=14⋅4<13⋅4421​=4⋅41​<3⋅41​

...

192=19⋅9<18⋅9921​=9⋅91​<8⋅91​

1102=110⋅10<19⋅101021​=10⋅101​<9⋅101​

⇒�=122+132+142+...+1102<11⋅2+12⋅3+13⋅4+...+19⋅10⇒A=221​+321​+421​+...+1021​<1⋅21​+2⋅31​+3⋅41​+...+9⋅101​

⇒�<1−12+12−13+...+19−110⇒A<1−21​+21​−31​+...+91​−101​

⇒�<1−110⇒A<1−101​

⇒�<910⇒A<109​

⇒�<1⇒A<1 (vì: 910<1109​<1)

Hình như bạn chép sai đề, mình sửa nhé :

\(S=\dfrac{5^2}{1.6}+\dfrac{5^2}{6.11}+\dfrac{5^2}{11.16}+...+\dfrac{5^2}{26.31}\\ =>\dfrac{S}{5}=\dfrac{5}{1.6}+\dfrac{5}{6.11}+\dfrac{5}{11.16}+...+\dfrac{5}{26.31}\\ =>\dfrac{S}{5}=\dfrac{6-1}{1.6}+\dfrac{11-6}{6.11}+\dfrac{16-11}{11.16}+...+\dfrac{31-26}{26.31}\\ =>\dfrac{S}{5}=1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{16}+...+\dfrac{1}{26}-\dfrac{1}{31}=1-\dfrac{1}{31}=\dfrac{30}{31}\\ =>S=\dfrac{30}{31}.5=\dfrac{150}{31}\)

\(\left(\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{98.99}+\dfrac{1}{99.100}\right).x=\dfrac{1}{5}\\ =>\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{98}-\dfrac{1}{99}+\dfrac{1}{99}-\dfrac{1}{100}\right).x=\dfrac{1}{5}\\ =>\left(\dfrac{1}{2}-\dfrac{1}{100}\right).x=\dfrac{1}{5}\\ =>\dfrac{49}{100}.x=\dfrac{1}{5}\\ =>x=\dfrac{1}{5}:\dfrac{49}{100}=\dfrac{1}{5}.\dfrac{100}{49}\\ =>x=\dfrac{20}{49}\)

ai cứu mik với

thì  a vuông góc với c nha

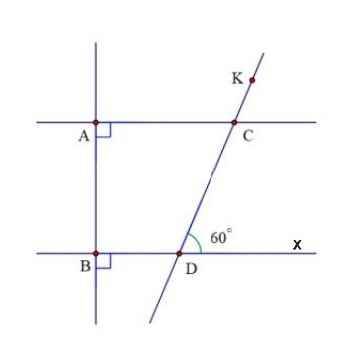
a) Do AC ⊥ AB

BD ⊥ AB

⇒ AC // BD

b) Do AC // BD

⇒ ∠ACD = ∠CDx = 60⁰ (so le trong)

Ta có:

∠ACK + ∠ACD = 180⁰ (kề bù)

⇒ ACK = 180⁰ - ACD

= 180⁰ - 60⁰

= 120⁰