Rút gọn biểu thức P=\(\dfrac{x+2}{x^2-4x+4}\):\(\left(\dfrac{6-x^2}{x^2-2x}-\dfrac{1}{2-x}+\dfrac{x+2}{x}\right)\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(x-y-z\right)^2-\left(x-y\right)^2+2x-yz\)
\(=\left(x-y\right)^2-2z\left(x-y\right)+z^2-\left(x-y\right)^2+2x-yz\)
\(=-2z\left(x-y\right)+z^2+2x-yz\)
\(=-2xz+2yz+z^2+2x-yz=z^2+2x-2xz+yz\)
Em nên viết bằng công thức toán học có biểu tượng\(\Sigma\) góc trái màn hình, để mọi người có thể hiểu đúng đề và trợ giúp tốt nhất cho tài khoản vip em nhé!

Xét ΔIDC có AB//DC
nên \(\dfrac{IA}{AD}=\dfrac{IB}{BC}\)
mà AD=BC
nên IA=IB
Xét ΔABC và ΔBAD có
AB chung
BC=AD
AC=BD
Do đó: ΔABC=ΔBAD
=>\(\widehat{CAB}=\widehat{DBA}\)
=>\(\widehat{OAB}=\widehat{OBA}\)
=>OA=OB
Ta có: OA+OC=AC
OB+OD=BD
mà OA=OB và AC=BD
nên OC=OD
ΔOCD cân tại O
mà ON là đường trung tuyến
nên ON\(\perp\)DC
ΔOAB cân tại O
mà OM là đường trung tuyến
nên OM\(\perp\)AB
mà AB//CD
nên OM\(\perp\)CD
Ta có: IA+AD=ID
IB+BC=IC
mà IA=IB và AD=BC
nên ID=IC
=>ΔIDC cân tại I
mà IN là đường trung tuyến
nên IN\(\perp\)DC
Ta có: OM\(\perp\)CD
ON\(\perp\)CD
mà OM,ON có điểm chung là O
nên O,M,N thẳng hàng(1)
Ta có: IN\(\perp\)DC
ON\(\perp\)CD
mà IN,ON có điểm chung là N
nên I,N,O thẳng hàng(2)
Từ (1),(2) suy ra I,M,O,N thẳng hàng

\(P=4x^2+2y^2-4xy-4x-8y+2050\\ =\left(4x^2-4xy+y^2\right)+y^2-4x-8y+2050\\ =\left(2x-y\right)^2-2.\left(2x-y\right).1+1^2+y^2-10y+2049\\ =\left(2x-y-1\right)^2+\left(y^2-10y+25\right)+2024\\ =\left(2x-y-1\right)^2+\left(y-5\right)^2+2024\ge2024\forall x,y\)
Dấu = xảy ra khi: \(\left(2x-y-1\right)^2=\left(y-5\right)^2=0\\ \Leftrightarrow\left(x;y\right)=\left(3;5\right)\)
Vậy min P = 2024 tại (x;y)=(3;5)

a: Xét ΔHEB vuông tại E và ΔHDC vuông tại D có
\(\widehat{EHB}=\widehat{DHC}\)(hai góc đối đỉnh)
Do đó: ΔHEB~ΔHDC
b: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{DAB}\) chung
Do đó: ΔADB~ΔAEC
=>\(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)
=>\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
=>\(AD\cdot AC=AB\cdot AE\)
Xét ΔADE và ΔABC có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
\(\widehat{DAE}\) chung
Do đó: ΔADE~ΔABC
=>\(\widehat{AED}=\widehat{ACB}\)
c: Ta có: ΔEBC vuông tại E
mà EN là đường trung tuyến
nên \(NE=\dfrac{BC}{2}\left(1\right)\)
ΔDBC vuông tại D
mà DN là đường trung tuyến
nên \(DN=\dfrac{BC}{2}\left(2\right)\)
Từ (1),(2) suy ra ND=NE
=>ΔNDE cân tại N
ΔNDE cân tại N
mà NM là đường trung tuyến
nên NM\(\perp\)DE

\(3\cdot\left(-35\right)\cdot\left(-37\right)-\left(-15\right)\cdot37\)
\(=105\cdot37+15\cdot37\)
\(=37\left(105+15\right)=37\cdot120=4440\)
4,(-35).15 -(-15)-37 5,(-154).(-235)+154.(-35) 6,(-25).(-17).4+(-20)

\(1.237.\left(-28\right)+28.137\)
\(=237.\left(-28\right)+28.137\)
\(=\left(-237\right).28+28.137\)
\(=28.\left[\left(-237\right)+137\right]\)
\(=28.\left(-100\right)\)
\(=-2800\)
1237 x (-28) + 28 x 137
= 1237 x (-28) - (-28) x 137
= (-28) x (1237 - 137)
= (-28) x 1100
= (-28) x (1000 + 100)
= (-28) x 1000 + (-28) x 100
= (-28000) + (-2800)
= (-30800)


A = a(b² + c²) + b(a² + c²) + c(a² + b²) + 3abc
= ab² + ac² + a²b + bc² + a²c + b²c + 3abc
= (ab² + a²b + abc) + (a²c + ac² + abc) + (b²c + bc² + abc)
= ab(a + b + c) + ac(a + c + b) + bc(b + c + a)
= (a + b + c)(ab + ac + bc)

\(22\cdot321+22\cdot456+11\cdot446\)
\(=22\cdot\left(321+456\right)+22\cdot223\)
\(=22\cdot777+22\cdot223=22\cdot1000=22000\)
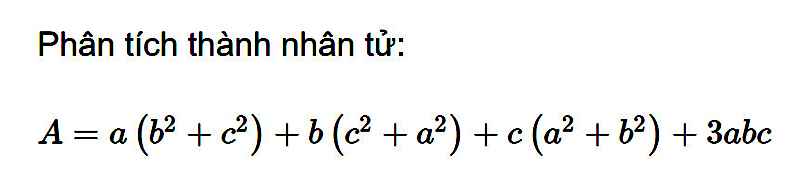
ĐKXĐ: \(x\notin\left\{0;2;-2\right\}\)
\(P=\dfrac{x+2}{x^2-4x+4}:\left(\dfrac{6-x^2}{x^2-2x}-\dfrac{1}{2-x}+\dfrac{x+2}{x}\right)\)
\(=\dfrac{x+2}{\left(x-2\right)^2}:\left(\dfrac{6-x^2}{x\left(x-2\right)}+\dfrac{1}{x-2}+\dfrac{x+2}{x}\right)\)
\(=\dfrac{x+2}{\left(x-2\right)^2}:\dfrac{6-x^2+x+\left(x+2\right)\left(x-2\right)}{x\left(x-2\right)}\)
\(=\dfrac{x+2}{\left(x-2\right)^2}\cdot\dfrac{x\left(x-2\right)}{6-x^2+x+x^2-4}\)
\(=\dfrac{x+2}{x-2}\cdot\dfrac{x}{x+2}=\dfrac{x}{x-2}\)