Cho nnn là một số nguyên dương. Hãy tìm tất cả các số nguyên dương nnn sao cho n2+1n^2 + 1n2+1 chia hết cho 2n+12n + 12n+1.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đề thi đánh giá năng lực

ĐKXĐ: \(20-x^2>0\)
=>\(x^2< 20\)
mà x nguyên
nên \(x\in\left\{0;1;-1;2;-2;3;-3;4;-4\right\}\)
=>Có 9 số nguyên

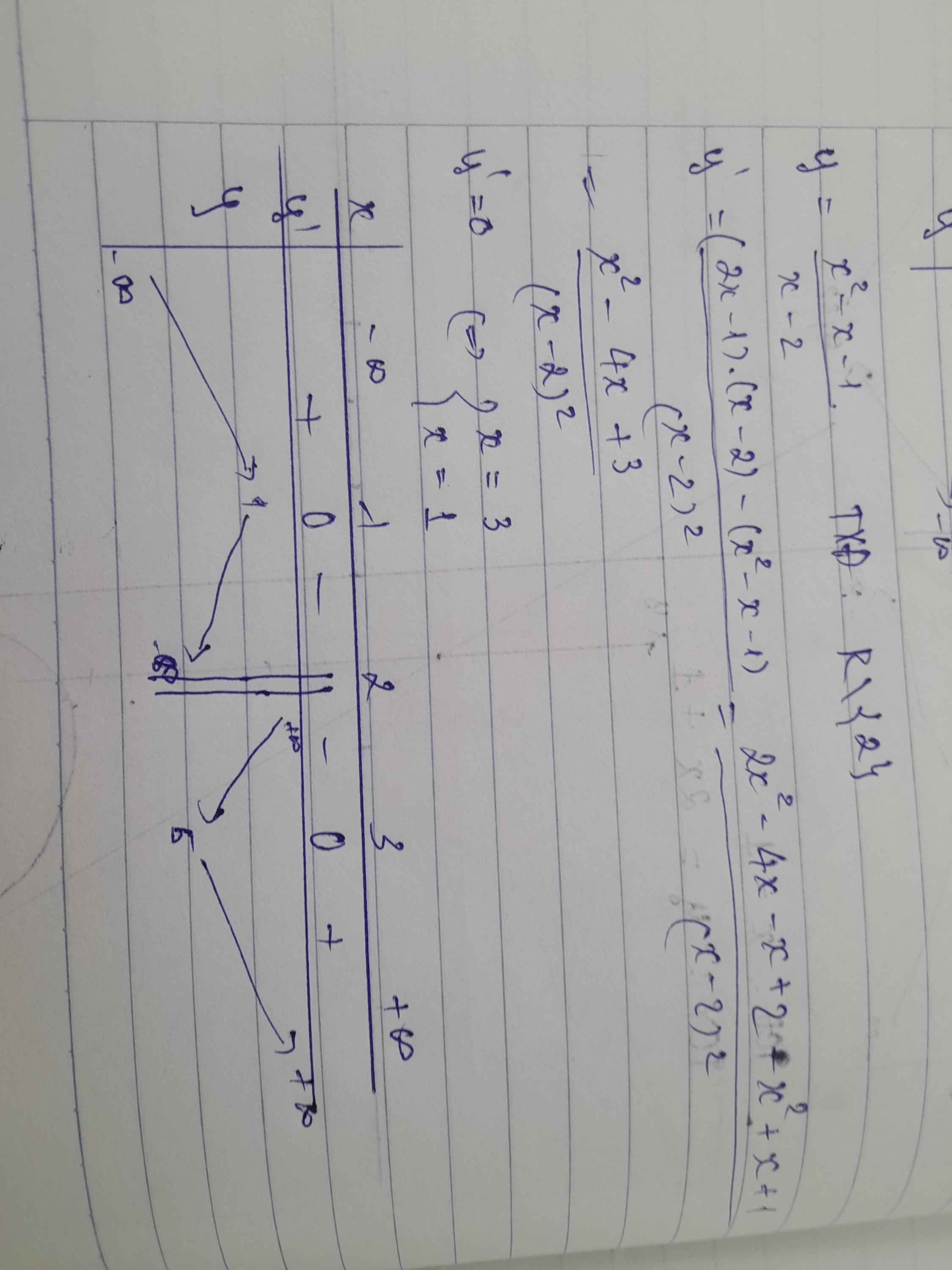
Tập xác định \(D=ℝ\backslash\left\{2\right\}\)
TCĐ: \(x=2\)
Có \(\dfrac{x^2-x-1}{x-2}=\dfrac{x^2-x-2+1}{x-2}=\dfrac{\left(x+1\right)\left(x-2\right)+1}{x-2}=\left(x+1\right)+\dfrac{1}{x-2}\)
nên đồ thị hàm số có tiệm cận xiên là đường \(y=x+1\)
Có \(y'=\dfrac{x^2-4x+3}{\left(x-2\right)^2}\)
\(y'=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
BBT

a) \(y=\dfrac{x+1}{x-2}\)
\(y'=-\dfrac{3}{\left(x-2\right)^2}< 0\forall x\inℝ\ \left\{2\right\}\)
=> hàm số nghịch biến trên \(\left(-\infty;2\right)\) và \(\left(2;+\infty\right)\)
b) \(y=\dfrac{2x+1}{x-1}\)
\(y'=-\dfrac{3}{\left(x-1\right)^2}< 0\forall x\inℝ\ \left\{1\right\}\)
=> hàm số nghịch biến trên \(\left(-\infty;1\right)\) và \((1;+\infty)\)

Kẻ AH\(\perp\)BC tại H, AK\(\perp\)SH tại K
\(\widehat{SB;\left(ABC\right)}=45^0\)
=>\(\widehat{BS;BA}=45^0\)
=>\(\widehat{SBA}=45^0\)
Xét ΔSAB vuông tại A có \(tanSBA=\dfrac{SA}{AB}\)
=>\(\dfrac{SA}{a}=tan45=1\)
=>SA=a
ΔABC vuông cân tại A
=>\(AB=AC=a\) và \(BC=\sqrt{AB^2+AC^2}=a\sqrt{2}\)
ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>\(AH=HB=HC=\dfrac{BC}{2}=\dfrac{a\sqrt{2}}{2}\)
Ta có: BC\(\perp\)AH
BC\(\perp\)SA
AH,SA cùng thuộc mp(SAH)
Do đó: BC\(\perp\)(SAH)
=>BC\(\perp\)AK
Ta có: AK\(\perp\)SH
AK\(\perp\)BC
SH,BC cùng thuộc mp(SBC)
Do đó: AK\(\perp\)(SBC)
=>AK là khoảng cách từ A đến mp(SBC)
ΔSAH vuông tại A
=>\(SH^2=SA^2+AH^2=a^2+\left(\dfrac{a\sqrt{2}}{2}\right)^2=a^2+\dfrac{1}{2}a^2=\dfrac{3}{2}a^2\)
=>\(SH=\dfrac{a\sqrt{6}}{2}\)
Xét ΔSAH vuông tại A có AK là đường cao
nên \(AK\cdot SH=SA\cdot AH\)
=>\(AK\cdot\dfrac{a\sqrt{6}}{2}=a\cdot\dfrac{a\sqrt{2}}{2}\)
=>\(AK\cdot\sqrt{6}=a\sqrt{2}\)
=>\(AK=a\sqrt{\dfrac{2}{6}}=a\sqrt{\dfrac{1}{3}}=\dfrac{a\sqrt{3}}{3}\)

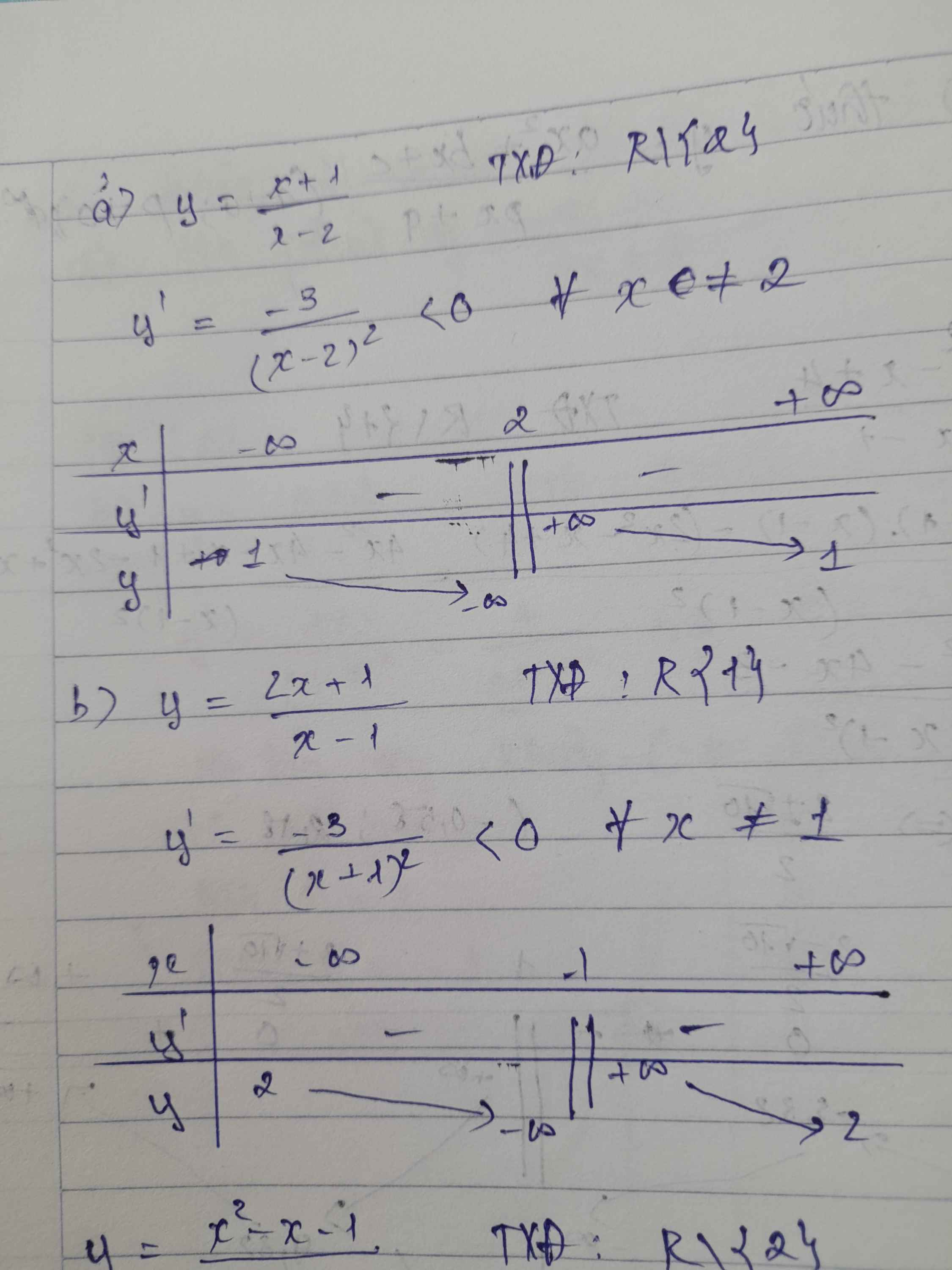


\(n^2+1⋮2n+1\)
\(\Leftrightarrow\exists k\inℕ^∗:n^2+1=k\left(2n+1\right)\)
\(\Leftrightarrow n^2-2kn+1-k=0\)
Có \(\Delta'=\left(-k^2\right)-\left(1-k\right)=k^2+k-1\)
Vì \(n\inℕ^∗\)nên \(\Delta'\) phải là số chính phương
\(\Leftrightarrow\exists l\inℕ^∗:k^2+k-1=l^2\)
\(\Leftrightarrow4k^2+4k-4=4l^2\)
\(\Leftrightarrow\left(4k^2+4k+1\right)-4l^2=5\)
\(\Leftrightarrow\left(2k+1\right)^2-\left(2l\right)^2=5\)
\(\Leftrightarrow\left(2k+2l+1\right)\left(2k-2l+1\right)=5\)
Vì \(k,l\inℕ^∗\) và \(2k+2l+1>2k-2l+1>0\) nên ta chỉ có 1 TH duy nhất là \(\left\{{}\begin{matrix}2k+2l+1=5\\2k-2l+1=1\end{matrix}\right.\) \(\Leftrightarrow k=l=1\)
Khi đó \(n^2+1=2n+1\)
\(\Leftrightarrow n^2=2n\)
\(\Leftrightarrow\left[{}\begin{matrix}n=0\left(loại\right)\\n=2\left(nhận\right)\end{matrix}\right.\)
Vậy \(n=2\) là số nguyên dương duy nhất thỏa mãn ycbt.