\(5^{n+3}-5^{n+1}=5^{12}.120\)

\(\Leftrightarrow5^n.5^3-5^n.5=5^{12}.120\Leftrightarrow5^n\left(5^3-5\right)=5^{12}.120\Leftrightarrow5^n.120=5^{12}.120\Leftrightarrow5^n=5^{12}\Rightarrow n=12\)

Diện tích xung quanh căn phòng là: 

`2 . h . (a+b) = 2 . 3 . (8 + 4) = 72 (m^2)`

Đổi `72m^2 = 7200dm^2`

Cần số viên gạch ống là: 

`7200 : 1,2 = 6000` (viên)

Đáp số: `6000` viên

`(5x - 1)^6 = 729`

`=> (5x - 1)^6 = 3^6`

`=> 5x - 1 = 3` hoặc `5x - 1 = -3`

`=> 5x = 4` hoặc `5x = -2`

`=> x = 4/5` hoặc `x = -2/5`

-------------------

`(2x + 1)^3 = -0,001`

`=> (2x + 1)^3 = (-0,1)^3`

`=> 2x + 1 = -0,1`

`=> 2x  = -1001/1000`

`=> x = -1001/2000`

a: \(2\cdot16>=2^n>4\)

=>\(2^5>=2^n>2^2\)

=>2<n<=5

mà n là số tự nhiên

nên \(n\in\left\{3;4;5\right\}\)

b: \(9\cdot27< =3^n< =243\)

=>\(243< =3^n< =243\)

=>\(3^n=243\)

=>n=5

c: \(27< 3^n< 3\cdot81\)

=>\(3^3< 3^n< 3^5\)

=>3<n<5

mà n là số tự nhiên

nên n=4

d: \(4^{15}\cdot9^{15}< 2^n\cdot3^n< 18^{16}\cdot2^{16}\)

=>\(36^{15}< 6^n< 36^{16}\)

=>\(6^{30}< 6^n< 6^{32}\)

=>30<n<32

mà n là số tự nhiên

nên n=31

\(a.2\cdot16\ge2^n>4\\ 2\cdot2^4\ge2^n>2^2\\ 2^5\ge2^n>2^2\\ 5\ge n>2\\ n\in\left\{3;4;5\right\}\\ b.9\cdot27\le3^n\le243\\ 3^2\cdot3^3\le3^n\le3^5\\ 3^5\le3^n\le3^5\\ n=5\\ c.27< 3^n< 3\cdot81\\ 3^3< 3^n< 3\cdot3^4\\ 3^3< 3^n< 3^5\\ 3< n< 5\\ n=4\\ d.4^{15}\cdot9^{15}< 2^n\cdot3^n< 18^{16}\cdot2^{16}\\ 36^{15}< 6^n< 36^{16}\\ \left(6^2\right)^{15}< 6^n< \left(6^2\right)^{16}\\ 6^{30}< 6^n< 6^{32}\\ n=31\)

\(a.\left(\dfrac{2}{33}\right)^n\cdot11^n=\dfrac{4}{9}\\ \left(\dfrac{2}{33}\cdot11\right)^n=\left(\dfrac{2}{3}\right)^2\\ \left(\dfrac{2}{3}\right)^n=\left(\dfrac{2}{3}\right)^2\\ n=2\\ b.\dfrac{125}{5^n}=5\\\dfrac{ 5^3}{5^n}=5\\ 5^{3-n}=5^1\\ 3-n=1\\ n=3-1\\ n=2\\ c.\dfrac{\left(-6\right)^n}{36}=-216\\ \dfrac{\left(-6\right)^n}{\left(-6\right)^2}=\left(-6\right)^3\\ =\left(-6\right)^{n-2}=\left(-6\right)^3\\ n-2=3\\ n=2+3\\ n=5\\ d.20^n:14^n=\dfrac{10}{7}\\ \left(\dfrac{20}{14}\right)^n=\dfrac{10}{7}\\ \left(\dfrac{10}{7}\right)^n=\left(\dfrac{10}{7}\right)^1\\ n=1\)

Bài 1:

a: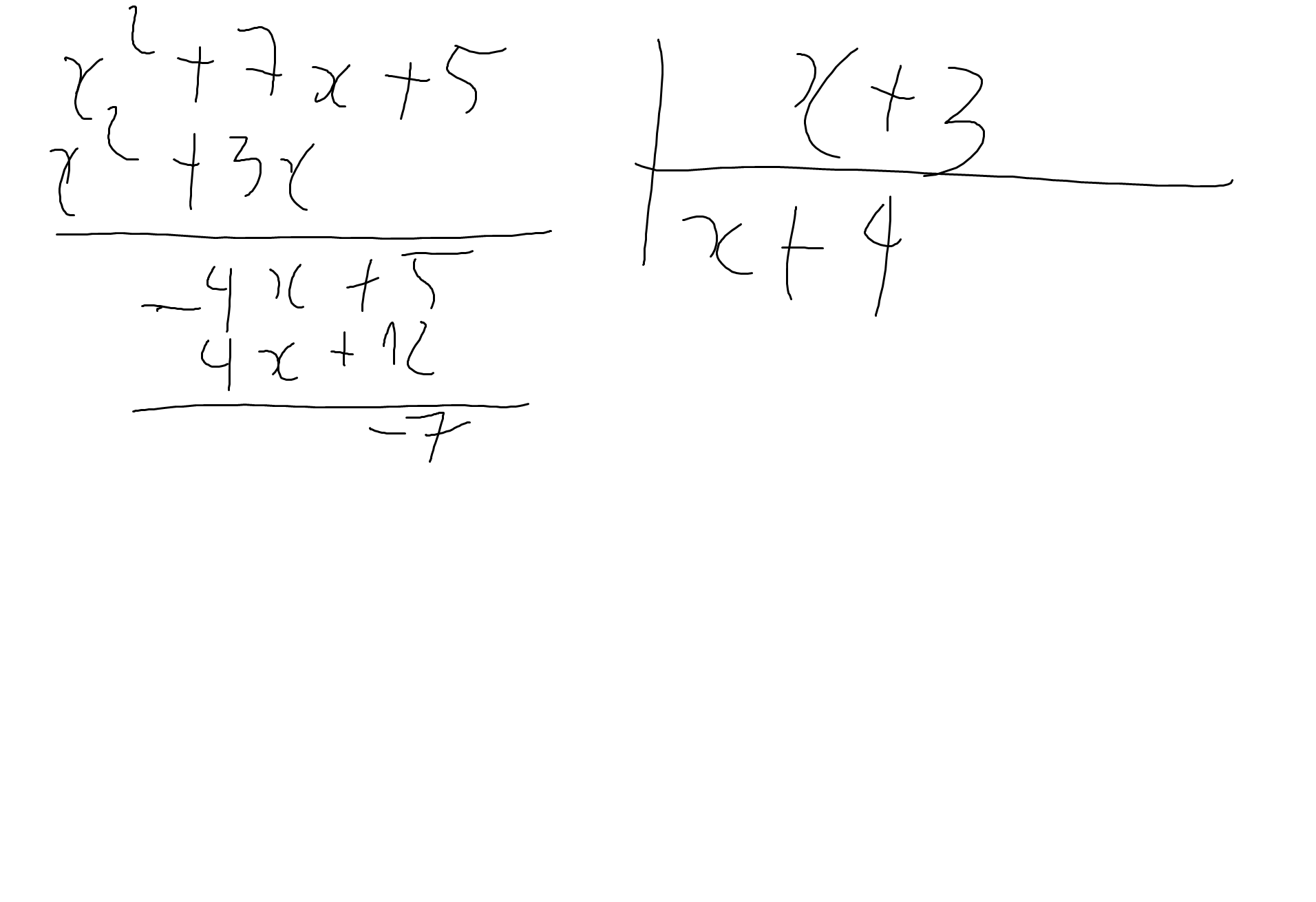 

b:

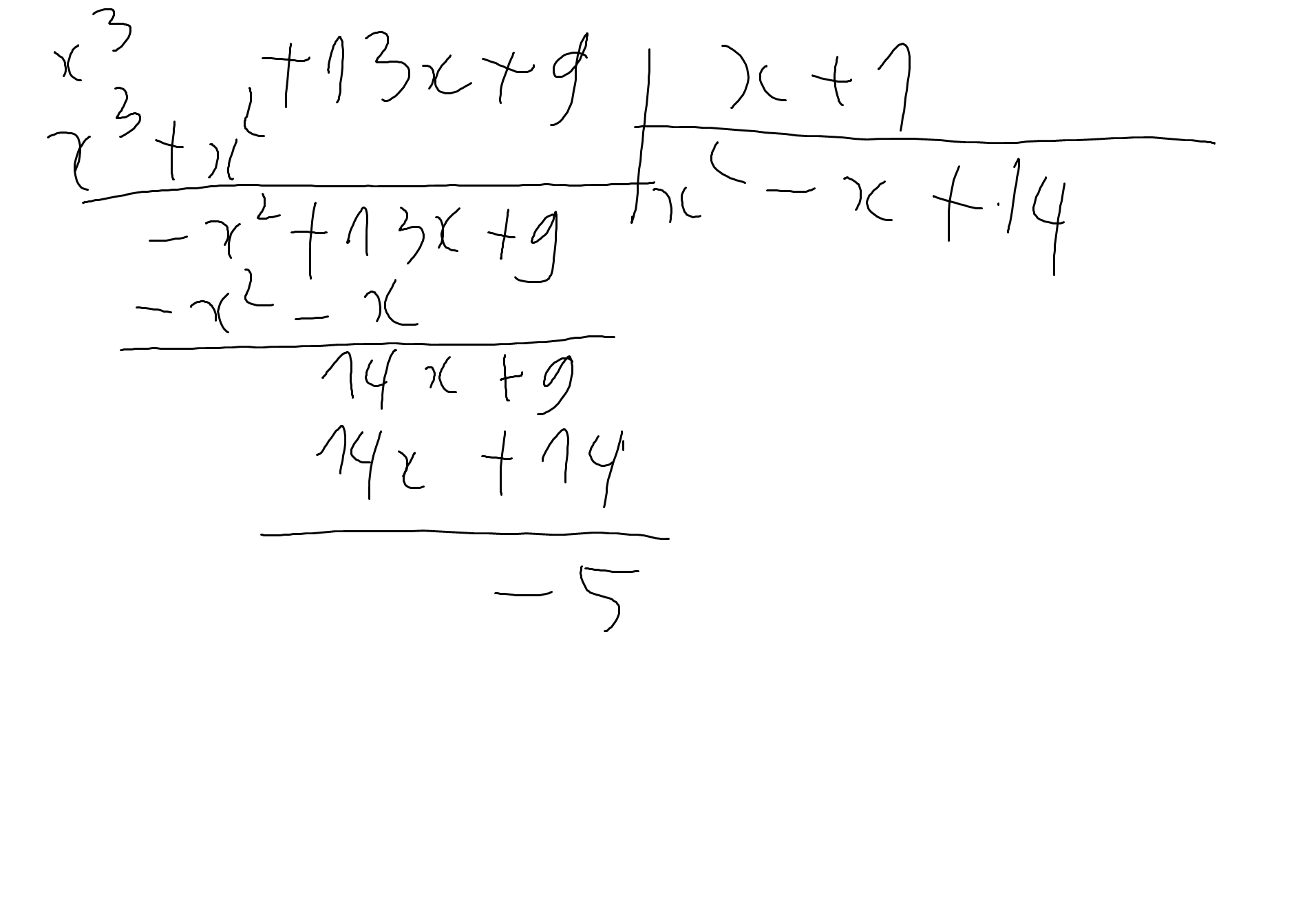
c:

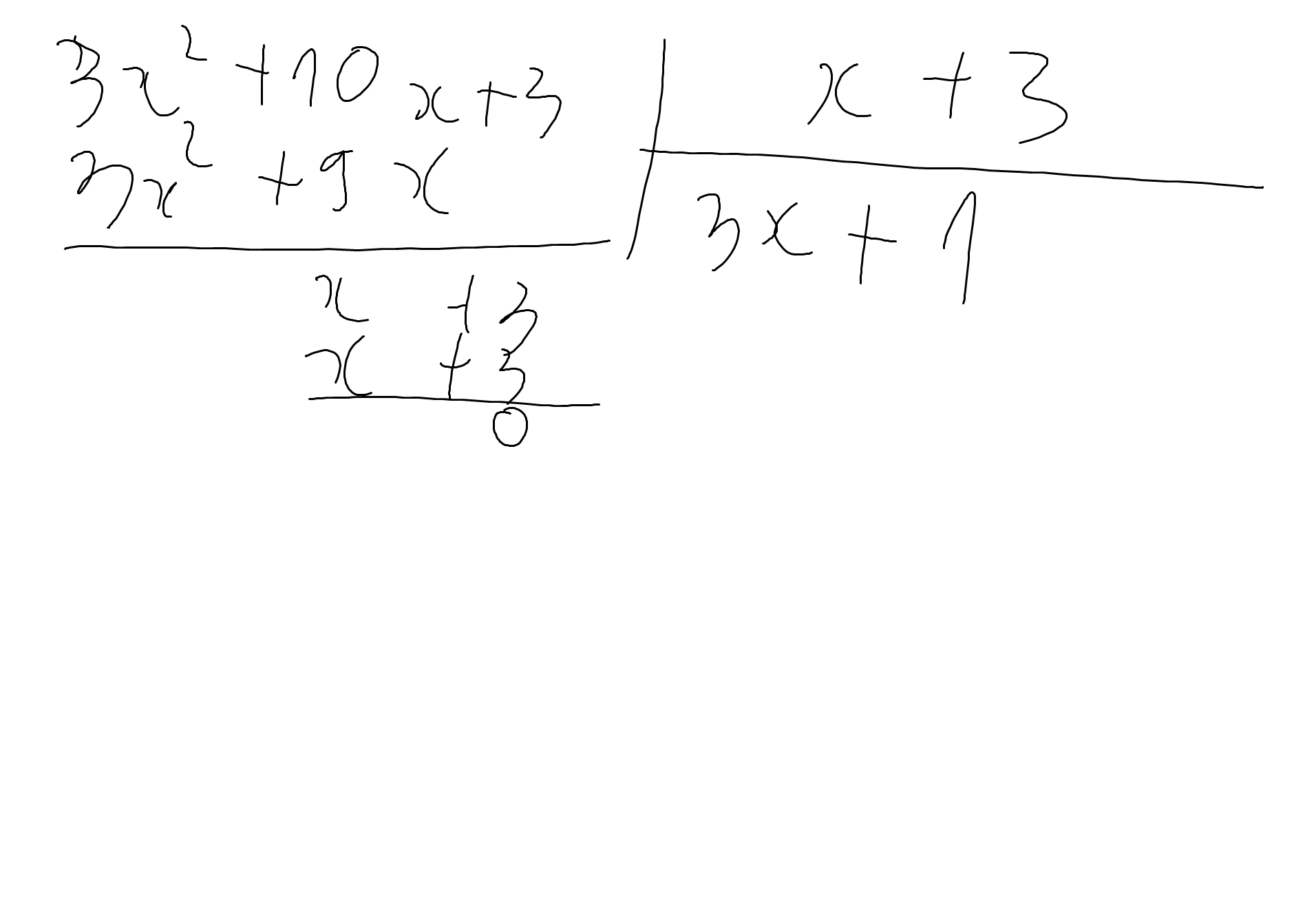
d:

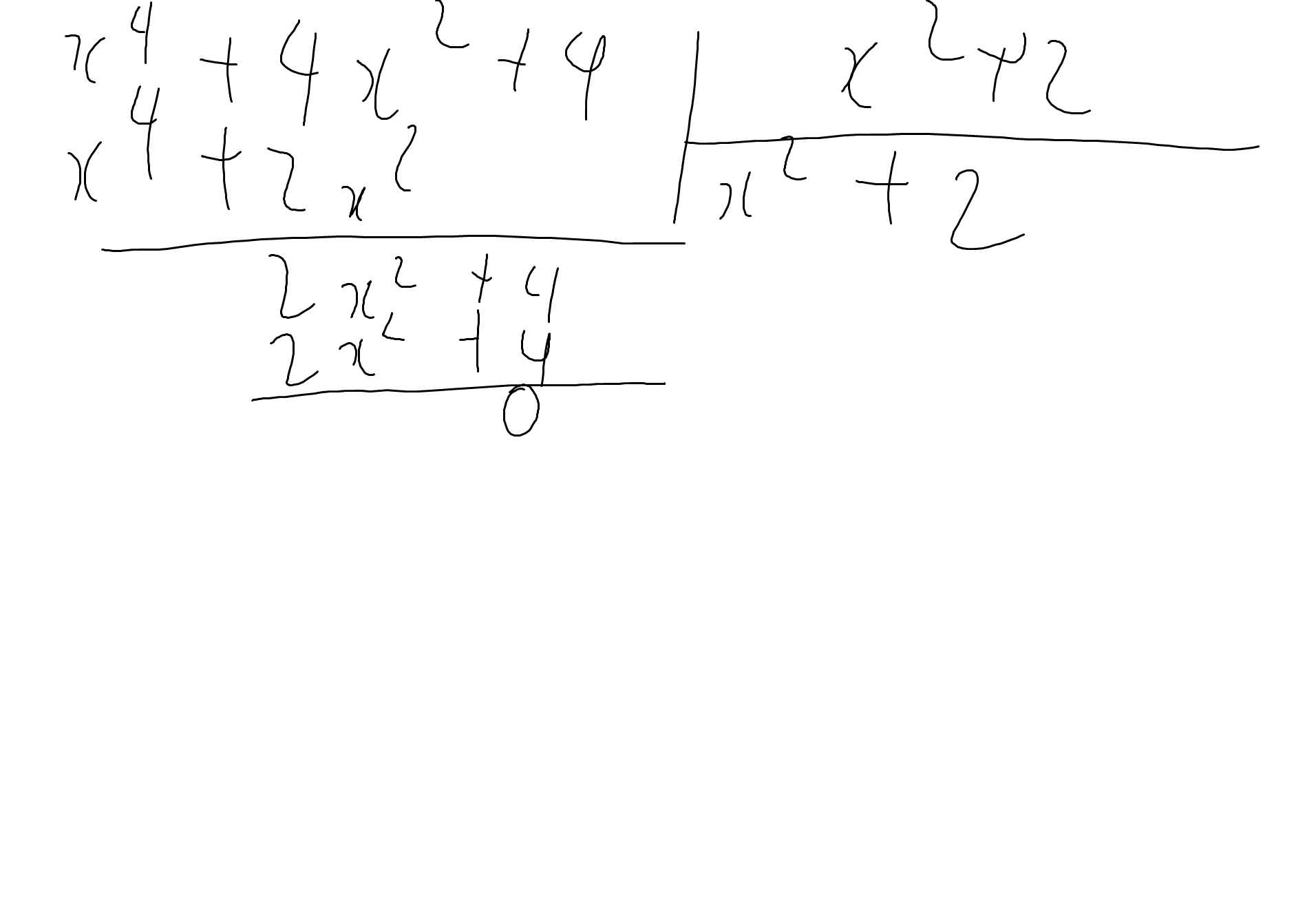
Bài 2:

a: Để \(x^2+4x+a⋮x-2\) thì \(x^2-2x+6x-12+a+12⋮x-2\)

=>a+12=0

=>a=-12

b: \(3x^2+7x+a⋮3x+1\)

=>\(3x^2+x+6x+2+a-2⋮3x+1\)

=>a-2=0

Đặt C(x)=0

=>\(x^2-2x+5=0\)

=>\(x^2-2x+1+4=0\)

=>\(\left(x-1\right)^2+4=0\)(vô lý)

=>C(x) vô nghiệm

Đặt D(x)=0

=>\(-x^2-6x-9=0\)

=>\(x^2+6x+9=0\)

=>\(\left(x+3\right)^2=0\)

=>x+3=0

=>x=-3

\(\dfrac{x-1}{65}+\dfrac{x-3}{63}=\dfrac{x-5}{61}+\dfrac{x-7}{59}\)

=>\(\left(\dfrac{x-1}{65}-1\right)+\left(\dfrac{x-3}{63}-1\right)=\left(\dfrac{x-5}{61}-1\right)+\left(\dfrac{x-7}{59}-1\right)\)

=>\(\dfrac{x-66}{65}+\dfrac{x-66}{63}-\dfrac{x-66}{61}-\dfrac{x-66}{59}=0\)

=>x-66=0

=>x=66

(2 - x)³ = 2

Lift hai vế lên độ 1/3:

2 - x = ³√2

Thêm x vào hai vế:

2 = x + ³√2

Trừ ³√2 khỏi hai vế:

x = 2 - ³√2

x ≈ 0,468

Vậy giá trị của x là khoảng 0,468.

Lưu ý rằng giá trị của x không phải là số nguyên. Nếu bạn tìm kiếm một giá trị gần đúng là số nguyên, tôi có thể tìm kiếm một giá trị gần đúng. Tuy nhiên, trong trường hợp này, giá trị chính xác của x đủ dùng.

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có

AB=AC

\(\widehat{BAD}\) chung

Do đó: ΔADB=ΔAEC

b: Sửa đề; AH là đường trung trực của BC

Xét ΔABC có

BD,CE là các đường cao

BD cắt CE tại H

Do đó: H là trực tâm của ΔABC

=>AH\(\perp\)BC

ΔABC cân tại A

mà AH là đường cao

nên AH là đường trung trực của BC

c: Gọi K là giao điểm của BN và CM

Ta có: AH là đường trung trực của BC

=>HB=HC

Xét ΔHBN và ΔHCM có

HB=HC

\(\widehat{BHN}=\widehat{CHM}\)(hai góc đối đỉnh)

HN=HM

Do đó: ΔHBN=ΔHCM

=>BN=CM và \(\widehat{HNB}=\widehat{HMC}\)

Ta có: \(\widehat{HNB}+\widehat{HNM}=\widehat{BNM}\)

\(\widehat{HMC}+\widehat{HMN}=\widehat{NMC}\)

mà \(\widehat{HNB}=\widehat{HMC};\widehat{HNM}=\widehat{HMN}\)

nên \(\widehat{BNM}=\widehat{CMN}\)

=>\(\widehat{KNM}=\widehat{KMN}\)

=>KM=KN

Ta có: KB+BN=KN

KC+CM=KM

mà KN=KM và BN=CM

nên KB=KC

=>K nằm trên đường trung trực của BC(1)

ta có: AB=AC

=>A nằm trên đường trung trực của BC(2)

ta có:HB=HC

=>H nằm trên đường trung trực của BC(3)

Từ (1),(2),(3) suy ra A,H,K thẳng hàng