Câu 1:

a.

$25x^2-10x+1=0$

$\Leftrightarrow (5x-1)^2=0\Leftrightarrow 5x-1=0$

$\Leftrightarrow x=\frac{1}{5}$

b.

$9x^4+8x^2-1=0$

$\Leftrightarrow (9x^4-x^2)+(9x^2-1)=0$

$\Leftrightarrow x^2(9x^2-1)+(9x^2-1)=0$

$\Leftrightarrow (9x^2-1)(x^2+1)=0$

$\Leftrightarrow (3x-1)(3x+1)(x^2+1)=0$

\(\Leftrightarrow \left[\begin{matrix} 3x+1=0\\ 3x-1=0\\ x^2+1=0\end{matrix}\right.\Leftrightarrow \Leftrightarrow \left[\begin{matrix} x=\frac{-1}{3}(\text{chọn})\\ x=\frac{1}{3}(\text{chọn})\\ x^2=-1<0(\text{loại})\end{matrix}\right.\)

c.

\(\left\{\begin{matrix}\ 2x-3y=1\\ -x+5y=3\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}\ 2x-3y=1\\ -2x+10y=6\end{matrix}\right.\)

$\Rightarrow (2x-3y)+(-2x+10y)=1+6$

$\Leftrightarrow 7y=7\Leftrightarrow y=1$

$x=5y-3=5-3=2$

Câu 3:

a. Bạn tự vẽ hình

b. PT hoành độ giao điểm $(P)$ và $(d)$:

$x^2=(2m+1)x+2$

$\Leftrightarrow x^2-(2m+1)x-2=0(*)$

Để $(d)$ cắt $(P)$ tại 2 điểm phân biệt $A(x_1,y_1), B(x_2,y_2)$ thì PT $(*)$ phải có 2 nghiệm phân biệt $x_1,x_2$

Điều này xảy ra khi: $\Delta=(2m+1)^2+8>0$

$\Leftrightarrow m\in\mathbb{R}$

Áp dụng định lý Viet:

\(\left\{\begin{matrix} x_1+x_2=2m+1\\ x_1x_2=-2\end{matrix}\right.\)

Khi đó:

$x_1^2+x_2^2=13$

$\Leftrightarrow (x_1+x_2)^2-2x_1x_2=13$

$\Leftrightarrow (2m+1)^2-2(-2)=13$

$\Leftrightarrow (2m+1)^2+4=13$

$\Leftrightarrow (2m+1)^3=9\Leftrightarrow 2m+1=\pm 3$

$\Leftrightarrow m=1$ hoặc $m=-2$ (tm)

là sao?

được em ạ

Pt có nghiệm khi:

\(\Delta=49-4\left(m-2\right)\ge0\)

\(\Leftrightarrow57-4m\ge0\)

\(\Rightarrow m\le\dfrac{57}{4}\)

Có vẻ đề bài bị lỗi hiện thị em ạ, em xem lại nhé.

Lỗi công thức rồi em. 

Đặt \(x^2=t\ge0\) ta được:

\(2t^2-3t-5=0\)

\(\Delta=9-4.2.\left(-5\right)=49\) nên pt có 2 nghiệm pb:

\(t_1=\dfrac{3+\sqrt{49}}{4}=\dfrac{5}{2}\) ; \(t_2=\dfrac{3-\sqrt{49}}{4}=-1< 0\) (loại)

\(\Rightarrow x^2=\dfrac{5}{2}\)

\(\Rightarrow x=\pm\dfrac{\sqrt{10}}{2}\)

Bài 4

a) Phương trình hoành độ giao điểm của (P) và (d):

x² = -4x - 3

⇔ x² + 4x + 3 = 0

Do a - b + c = 1 - 4 + 3 = 0 nên phương trình có hai nghiệm:

x₁ = -1; x₂ = -3

*) x₁ = -1

y = (-1)² = 1

*) x₂ = -3

y = (-3)² = 9

Vậy tọa độ giao điểm của (P) và (d) là:

(-1; 1); (-3; 9)

b) Do (d) đi qua điểm A(2; 3) nên:

2a + b = 3

⇔ b = 3 - 2a (1)

Do (d) đi qua điểm B(1; 2) nên:

a + b = 2 (2)

Thế (1) vào (2), ta có:

a + 3 - 2a = 2

⇔ -a = 2 - 3

⇔ -a = -1

⇔ a = 1

Thế a = 1 vào (1), ta có:

b = 3 - 2.1 = 1

Vậy (d): y = x + 1

Bài 8:

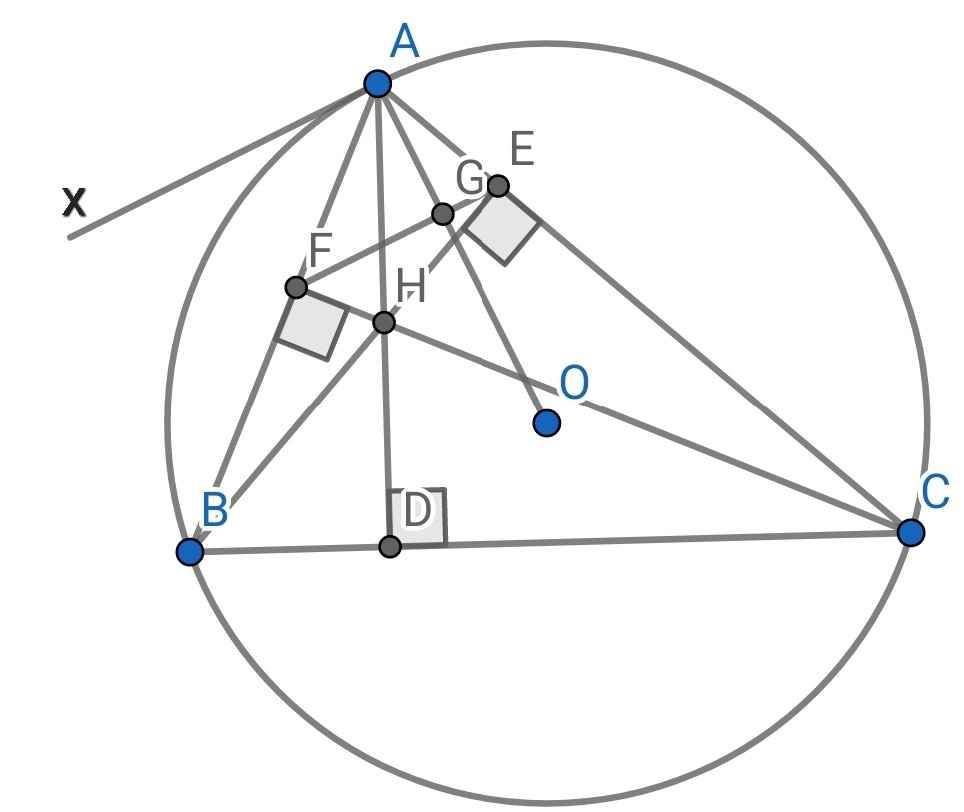
a) Xét tứ giác AEHF có:

∠HEA = ∠HFA = 90⁰ (gt)

⇒ ∠HEA + ∠HFA = 90⁰ + 90⁰ = 180⁰

⇒ AEHF nội tiếp

b) Xét tứ giác BFEC có:

∠BFC = ∠BEC = 90⁰ (gt)

⇒ F, E cùng nhìn cạnh BC dưới một góc 90⁰

⇒ BFEC nội tiếp

c) Qua A vẽ tia Ax ⊥ OA

⇒ Ax là tiếp tuyến của (O) tại A

⇒ ∠xAB = ∠ACB (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung AB của (O))

Lại có:

∠ACB + ∠HBD = 90⁰ (∆EBC vuông tại E)

∠BHD + ∠HBD = 90⁰ (∆BHD vuông tại D)

⇒ ∠ACB = ∠BHD

Mà ∠BHD = ∠AHE (đối đỉnh)

⇒ ∠ACB = ∠AHE

Do AEHF nội tiếp (cmt)

⇒ ∠AHE = ∠AFE (hai góc nội tiếp cùng chắn cung AE)

⇒ ∠ACB = ∠AFE

Mà ∠ACB = ∠xAB (cmt)

⇒ ∠AFE = ∠xAB

Mà ∠AFE và ∠xAB là hai góc đồng vị

⇒ EF // Ax

Mà Ax ⊥ OA

⇒ OA ⊥ EF

Em nên gõ đề bài bằng công thức toán học biểu tượng \(\Sigma\) góc trái màn hình.