Cho 50 điểm trong đó chỉ có 4 điểm thẳng hàng, cứ qua hai điểm vẽ được một đường thẳng Hỏi có tất cả bao nhiêu đường thẳng?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đức đã đi đc số phần quãng đường là
1/7+6/21+3/12=19/28(quãng đường)
=>Đức đã đi đc 19/28 quãng đường

\(\dfrac{3}{4}\) x X + \(\dfrac{3}{10}\) = \(\dfrac{7}{25}\)
\(\dfrac{3}{4}\) x X = \(\dfrac{7}{25}-\dfrac{3}{10}\)
\(\dfrac{3}{4}\) x \(X\) = \(\dfrac{-1}{50}\)
X = \(\dfrac{-1}{50}\):\(\dfrac{3}{4}\)
X = \(\dfrac{-4}{150}\)
3/4 x X + 3/10 = 7/25
3/4 x X =7/25-3/10
3/4 x X=-1/50
X=-1/50:3/4
X=-7/25
cho xin 5 sao đi

\(A=\dfrac{3^{2022}+2}{3^{2022}-1}=\dfrac{3^{2022}-1+3}{3^{2022}-1}=1+\dfrac{3}{3^{2022}-1}\)
\(B=\dfrac{3^{2022}}{3^{2022}-3}=\dfrac{3^{2022}-3+3}{3^{2022}-3}=1+\dfrac{3}{3^{2022}-3}\)
Vì \(3^{2022}-1>3^{2022}-3\)
nên \(\dfrac{3}{3^{2022}-1}< \dfrac{3}{3^{2022}-3}\)
=>\(1+\dfrac{3}{3^{2022}-1}< 1+\dfrac{3}{2^{2022}-3}\)
=>A<B

Với các số dương \(a;b;n\) sao cho \(a>b\) ta luôn có: \(\dfrac{a}{b}>\dfrac{a+n}{b+n}\)
Thật vậy, do \(a>b\Rightarrow an>bn\Rightarrow ab+an>ab+bn\)
\(\Rightarrow a\left(b+n\right)>b\left(a+n\right)\)
\(\Rightarrow\dfrac{a}{b}>\dfrac{a+n}{b+n}\)
Áp dụng:
Do \(3^{2022}>3^{2022}-3>0\) và \(2>0\) nên:
\(\dfrac{3^{2022}}{3^{2022}-3}>\dfrac{3^{2022}+2}{3^{2022}-3+2}\Rightarrow\dfrac{3^{2022}}{3^{2022}-3}>\dfrac{3^{2022}+2}{3^{2022}-1}\)
Vậy \(B>A\)

LG
Ngày 3 làm còn lại 3 bài tương ứng với số phần là
1-3/5=2/5
Ngày 3 và 2 làm số bài là:
3:2/5=15/2
an làm số bài là
15/2:(1-1/3)=45/4 bài tập
$_$ tích cho mk nha!!!

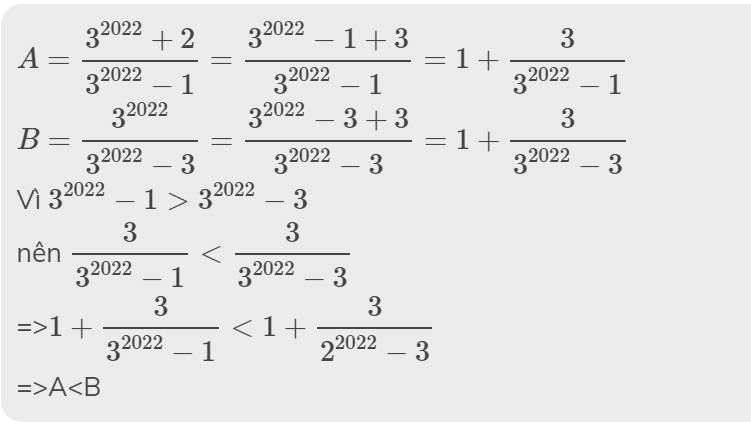
\(\dfrac{2^{2024}+2^{2023}+2^{2022}+2^{2021}}{60}=\dfrac{2^{2021}\left(2^3+2^2+2+1\right)}{60}=\dfrac{2^{2021}.15}{60}\)
\(=\dfrac{2^{2019}.2^2.15}{60}=\dfrac{2^{2019}.60}{60}=2^{2019}\)
\(\Rightarrow n=2019\)


\(\dfrac{2^4\cdot125}{2^7\cdot50}=\dfrac{2^4\cdot5^3}{2^8\cdot5^2}=\dfrac{5}{2^4}=\dfrac{5}{16}\)


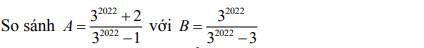
Số điểm còn lại là 50-4=46(điểm)
TH1: Lấy 1 điểm trong 4 điểm thẳng hàng, lấy 1 điểm trong 46 điểm còn lại
=>Có \(46\cdot4=184\left(đường\right)\)
TH2: Lấy 2 điểm bất kì trong 4 điểm thẳng hàng
=>Có 1 đường thẳng
TH3: Lấy 2 điểm bất kì trong 46 điểm còn lại
=>Có \(C^2_{46}=1035\left(đường\right)\)
Số đường thẳng tất cả là:
1035+1+184=1220(đường)