
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nếu giảm giá \(\dfrac{2}{5}\) thì giảm số tiền là:
27500\(\cdot\dfrac{2}{5}=11000\) (đồng)
Nếu giảm giá \(\dfrac{2}{5}\) thì giá bán mới của quyển sách đó là:
27500-11000=16500 (đồng)
Vậy nếu giảm giá \(\dfrac{2}{5}\) thì giá bán mới của quyển sách là 16500 đồng.
Lời giải:
Nếu giảm giá 2/5 thì giá bán mới bằng $1-\frac{2}{5}=\frac{3}{5}$ giá cũ.
Giá bán mới của quyển sách là:
$27500\times \frac{3}{5}=16500$ (đồng)

Vì 5\(x\) là số lẻ với \(\forall\) \(x\in\) N nên 5\(^x\) + 12y = 26 ⇔ 12y là số lẻ
⇒ 12y = 1 ⇒ 12y = 120 ⇒ y = 0
Thay y = 0 vào biểu thức: 5\(x\) + 12y = 26 ta có
5\(x\) + 120 = 26
5\(^x\) + 1 = 26
5\(^x\) = 26 - 1
5\(x\) = 25
5\(x\) = 52
\(x\) = 2
Vậy (\(x;y\)) = (2; 0)
Vì 5
�
x là số lẻ với
∀
∀
�
∈
x∈ N nên 5
�
x
+ 12y = 26 ⇔ 12y là số lẻ
⇒ 12y = 1 ⇒ 12y = 120 ⇒ y = 0
Thay y = 0 vào biểu thức: 5
�
x + 12y = 26 ta có
5
�
x + 120 = 26
5
�
x
+ 1 = 26
5
�
x
= 26 - 1
5
�
x = 25
5
�
x = 52
�
x = 2
Vậy (
�
;
�
x;y) = (2; 0)

Gọi số học sinh lớp 6A1;6A2;6A3 lần lượt là a(bạn),b(bạn),c(bạn)
(ĐK: \(a,b,c\in Z^+\))
Tỉ số giữa số học sinh lớp 6A2 và 6A1 là 8:9 nên \(\dfrac{a}{9}=\dfrac{b}{8}\)
=>\(\dfrac{a}{18}=\dfrac{b}{16}\left(1\right)\)
Tỉ số giữa số học sinh lớp 6A3 và 6A2 là 17:16 nên \(\dfrac{c}{17}=\dfrac{b}{16}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{a}{18}=\dfrac{b}{16}=\dfrac{c}{17}\)
Tổng số học sinh là 102 bạn nên a+b+c=102
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được;
\(\dfrac{a}{18}=\dfrac{b}{16}=\dfrac{c}{17}=\dfrac{a+b+c}{18+16+17}=\dfrac{102}{51}=2\)
=>\(a=18\cdot2=36;b=16\cdot2=32;c=17\cdot2=34\)
vậy: số học sinh lớp 6A1;6A2;6A3 lần lượt là 36 bạn;32 bạn; 34 bạn

Ta có:
122<11.2;132<12.3;...;11002<199.100122<11.2;132<12.3;...;11002<199.100
Đặt:
A=1+122+132+...+11002�=1+122+132+...+11002
→A<1+11.2+12.3+...+199.100=1+11−12+12−13+...+199−1100=2−1100<2→�<1+11.2+12.3+...+199.100=1+11-12+12-13+...+199-1100=2-1100<2
→1+122+132+...+11002<2→1+122+132+...+11002<2
→→đpcm
nhớ tick cho mik nha
cách 2 :
Đặt 1+1/2^2+1/3^2+...+1/100^2=A
Có A<1+1/1.2+1/2.3+1/3.4+....+1/99.100
=>A<1+1-1/2+1/2-1/3+1/3-1/4+....+1/99-1/100
=>A<1+1-1/100
=>A<2-1/100<2
nhớ tickkk

p là số nguyên tố lớn hơn 3
=>p=3k+1 hoặc p=3k+2
TH1: p=3k+1
8p+1=8(3k+1)+1=24k+8+1=24k+9 chia hết cho 3
=>Loại
=>p=3k+2
\(4p+1=4\left(3k+2\right)+1=12k+8+1\)
\(=12k+9=3\left(4k+3\right)⋮3\)
=>4p+1 là hợp số
Do p là số nguyên tố lớn hơn 3 nên p = 3k + 1 hoặc p = 3k + 2 (k ∈ ℕ*)
Khi p = 3k + 1
⇒ 8p + 1 = 8(3k + 1) + 1
= 24k + 8 + 1
= 24k + 9
= 3.(8k + 3) ⋮ 3
⇒ 8p + 1 là hợp số (loại vì theo đề bài 8p + 1 là số nguyên tố)
⇒ p = 3k + 2
⇒ 4p + 1 = 4(3k + 2) + 1
= 12k + 8 + 1
= 12k + 9
= 3(4k + 3) ⋮ 3
Vậy 4p + 1 là hợp số

Tổng vận tốc hai xe là 42+18=60(km/h)
Hai xe gặp nhau sau 120:60=2(giờ)
Hai người gặp nhau lúc:
8h30p+2h=10h30p
Nơi gặp nhau cách A:
\(2\cdot42=84\left(km\right)\)
Tổng vận tốc hai xe là 42+18=60(km/h)
Hai xe gặp nhau sau 120:60=2(giờ)
Hai người gặp nhau lúc:
8h30p+2h=10h30p
Nơi gặp nhau cách A:
2⋅42=84(��)2.42=84(km)
Đ/S:....

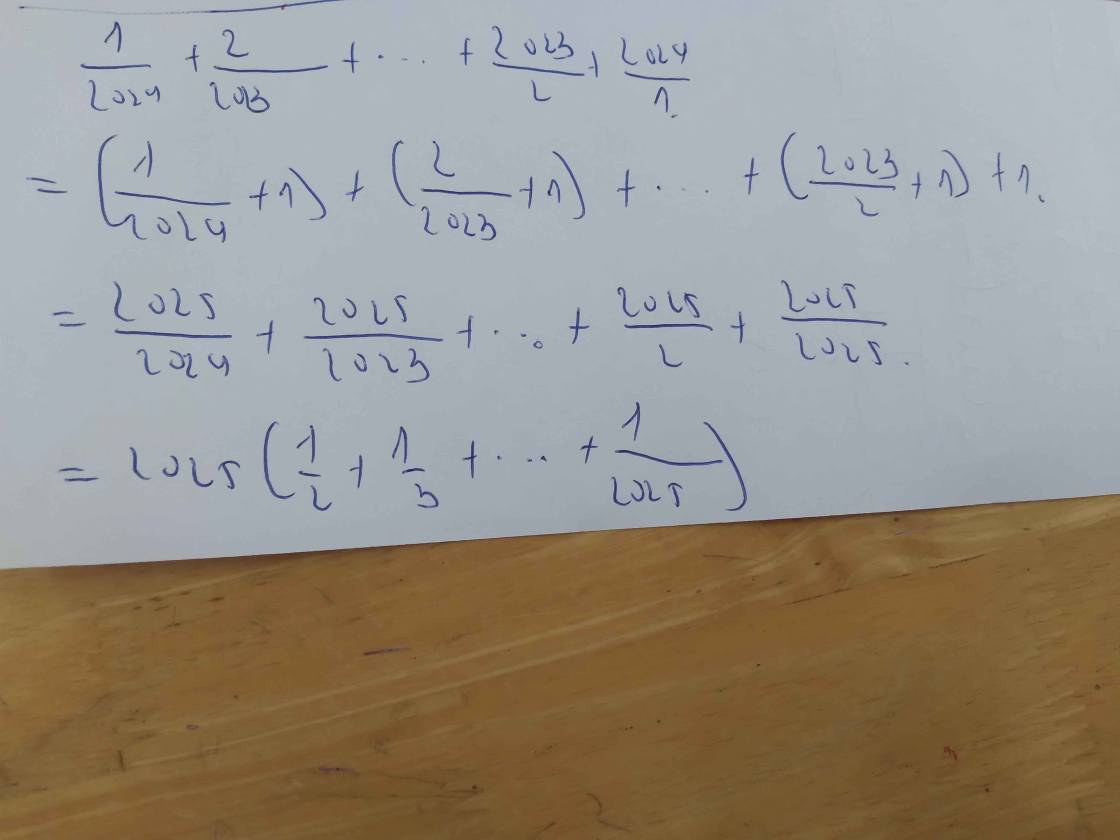
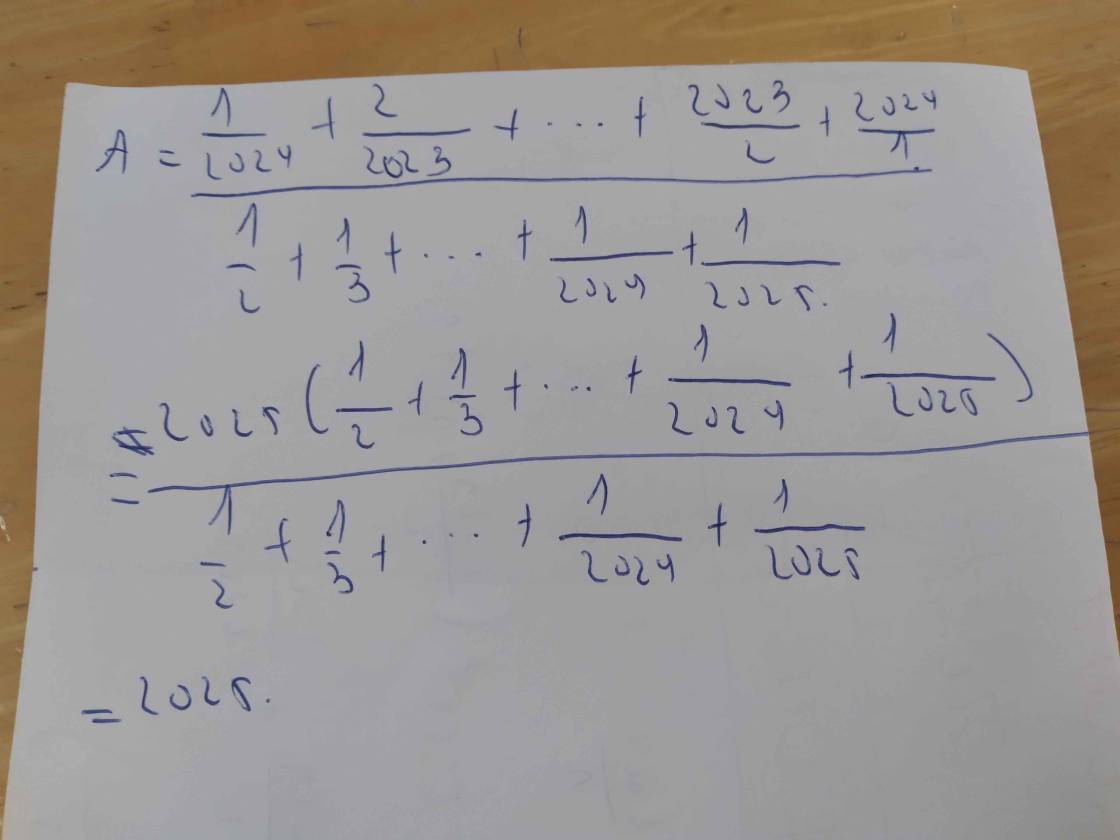
\(A=\dfrac{\dfrac{1}{2024}+\dfrac{2}{2023}+...+\dfrac{2023}{2}+\dfrac{2024}{1}}{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2024}+\dfrac{1}{2025}}\)
\(=\dfrac{\left(\dfrac{1}{2024}+1\right)+\left(\dfrac{2}{2023}+1\right)+...+\left(\dfrac{2023}{2}+1\right)+1}{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2024}+\dfrac{1}{2025}}\)
\(=\dfrac{\dfrac{2025}{2024}+\dfrac{2025}{2023}+...+\dfrac{2025}{2}+\dfrac{2025}{2025}}{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2024}+\dfrac{1}{2025}}\)
\(=\dfrac{2025\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2024}+\dfrac{1}{2025}\right)}{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2024}+\dfrac{1}{2025}}=2025\)