Cho tam giác ABC vuông tại A, vẽ tia phân giác BD . Kẻ DE vuông góc với BC (
E thuộc BC ). Gọi F là giao điểm của BA và ED . Chứng minh rằng:
a) Tam giác BED bằng tam giác BAD .
b) Tam BCF cân tại B .
c) BD là đường trung tuyến của tam giác BCF .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


chỉ có làm thì mới có ăn,ko làm mà đòi có ăn thì ăn cứt,ăn đb nhá



Nếu giảm chiều dài đi 3 lần và chiều rộng 2 lần thì diện tích giảm số lần là: 3 x 2 = 6 lần
Diện tích hình vuông là:
486 : 6 = 81 cm vuông

????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
Gọi số đã cho là AB, trong đó A và B lần lượt là chữ số hàng chục và hàng đơn vị của số đã cho.
Theo phương trình trong câu hỏi, chúng ta có:
10A + B = 6 × (100A + 10B + 4).
Mở rộng phương trình ta được:
10A + B = 600A + 60B + 24.
Kết hợp các thành phần của cùng một vị trí, ta có:
9A + 11B = 24.
Với A từ 0 đến 9, ta kiểm tra giá trị B tương ứng và tìm ra rằng A = 4 và B = 6 là giải pháp duy nhất. Vì vậy, số cần tìm là 46.


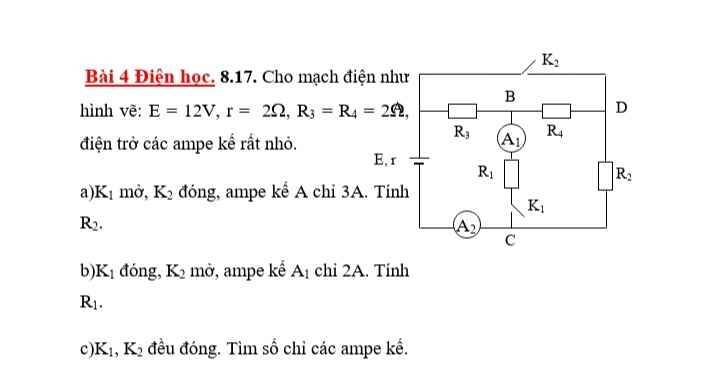
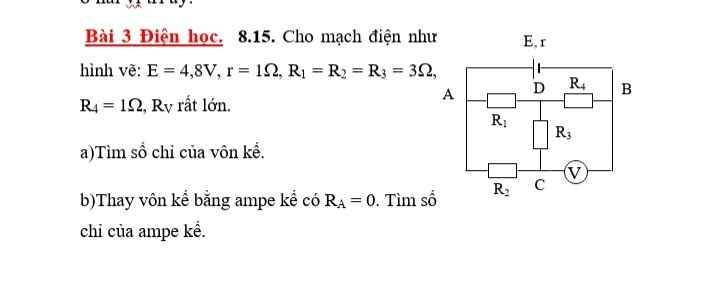 giúp em vs nhaa mn em cảm ơn trước ạ
giúp em vs nhaa mn em cảm ơn trước ạ