Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Haiđường cao BM và CN giao nhau tại H.a. Chứng minh: Tứ giác BNMC nội tiếp. Xác định tâm I| của đường tròn ngoại tiếp tứ giác này.b. Chứng minh: tam giác AMN và tam giác ABC đồng dạng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số dụng cụ mỗi ngày phải làm là x(dụng cụ), gọi số ngày phải hoàn thành là y(ngày)
(Điều kiện: \(x\in Z^+;y>0\))
Người thứ nhất làm vượt mức mỗi ngày 3 dụng cụ nên làm xong công việc sớm 2 ngày nên ta có:
(x+3)(y-2)=xy
=>xy-2x+3y-6=xy
=>-2x+3y=6(1)
Người thứ hai làm kém định mức mỗi ngày 3 dụng cụ nên hoàn thành lâu hơn 3 ngày nên ta có:
(x-3)(y+3)=xy
=>xy+3x-3y-9=xy
=>3x-3y=9
=>x-y=3(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}-2x+3y=6\\x-y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2x+3y=6\\2x-2y=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2x+3y+2x-2y=6+6\\x-y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=12\\x=y+3=15\end{matrix}\right.\left(nhận\right)\)
Số dụng cụ được giao là 12*15=180(dụng cụ)

a: 5-(x-6)=4(2x-3)
=>8x-12=5-x+6
=>8x-12=-x+11
=>9x=23
=>\(x=\dfrac{23}{9}\)
b: \(3-4x+24+6x=x+27+3x\)
=>\(4x+27=2x+27\)
=>2x=0
=>x=0
c: \(\left(x+5\right)\left(x-1\right)=2x\left(x-1\right)\)
=>\(2x\left(x-1\right)-\left(x+5\right)\left(x-1\right)=0\)
=>\(\left(x-1\right)\left(2x-x-5\right)=0\)
=>(x-1)(x-5)=0
=>\(\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)
d: \(5\left(3x-2\right)-4\left(5-3x\right)=1\)
=>\(15x-10-20+12x=1\)
=>27x=1+30=31
=>\(x=\dfrac{31}{27}\)

a: Xét \(\left(\dfrac{MC}{2}\right)\) có
ΔCDM nội tiếp
CM là đường kính
Do đó: ΔCDM vuông tại D
=>BD\(\perp\)DC tại D
Xét tứ giác ABCD có \(\widehat{CDB}=\widehat{CAB}=90^0\)
nên ABCD là tứ giác nội tiếp
b: ta có: ABCD là tứ giác nội tiếp
=>\(\widehat{ABD}=\widehat{ACD}\)

1: Ta có: ΔOCD cân tại O
mà OK là đường trung tuyến
nên OK\(\perp\)CD
Xét tứ giác OKMB có \(\widehat{OKM}+\widehat{OBM}=90^0+90^0=180^0\)
nên OKMB là tứ giác nội tiếp
2: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM là đường trung trực của AB
=>OM\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2\)
=>\(OH\cdot OM=R^2\left(3\right)\)
Xét ΔOHN vuông tại H và ΔOKM vuông tại K có
\(\widehat{HON}\) chung
Do đó: ΔOHN~ΔOKM
=>\(\dfrac{OH}{OK}=\dfrac{ON}{OM}\)
=>\(OK\cdot ON=OH\cdot OM\left(4\right)\)
Từ (3) và (4) suy ra \(OK\cdot ON=R^2\)
=>\(OK\cdot ON=OC^2\)
=>\(\dfrac{OK}{OC}=\dfrac{OC}{ON}\)
Xét ΔOKC và ΔOCN có
\(\dfrac{OK}{OC}=\dfrac{OC}{ON}\)
\(\widehat{KOC}\) chung
Do đó: ΔOKC~ΔOCN
=>\(\widehat{OCN}=\widehat{OKC}\)
=>\(\widehat{OCN}=90^0\)
=>NC là tiếp tuyến của (O)

Gọi số học sinh của lớp 10 Toán và lớp 10 Tin theo kế hoạch lần lượt là x(bạn) và y(bạn)
(Điều kiện: \(x,y\in Z^+\))
Tổng số học sinh là 63 bạn nên x+y=63(1)
Số học sinh lớp Toán sau khi chuyển 3 bạn là x-3(bạn)
Số học sinh lớp Tin sau khi nhận thêm 3 bạn là y+3(bạn)
4 lần số học sinh lớp toán bằng 5 lần số học sinh lớp tin nên 4(x-3)=5(y+3)
=>4x-12=5y+15
=>4x-5y=27(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}x+y=63\\4x-5y=27\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x+4y=252\\4x-5y=27\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9y=225\\x+y=63\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=25\\x=63-25=38\end{matrix}\right.\left(nhận\right)\)
vậy: số học sinh của lớp 10 Toán và lớp 10 Tin theo kế hoạch lần lượt là 38 bạn và 25 bạn

Xét (O) có
\(\widehat{BAM}\) là góc nội tiếp chắn cung BM
\(\widehat{CAM}\) là góc nội tiếp chắn cung CM
\(\widehat{BAM}=\widehat{CAM}\)
Do đó: \(sđ\stackrel\frown{BM}=sđ\stackrel\frown{CM}\)
=>BM=CM
=>M nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OM là đường trung trực của BC
=>OM đi qua trung điểm của BC
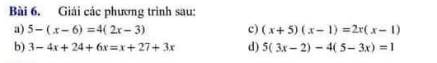



a) Tứ giác BNMC có:
\(\widehat{BNC}=\widehat{BMC}=90^0\) (do BM và CN là hai đường cao của \(\Delta ABC\))
\(\Rightarrow M,N\) cùng nhìn BC dưới một góc \(90^0\)
\(\Rightarrow BNMC\) nội tiếp
*) Gọi \(I\) là trung điểm của BC
\(\Delta BMC\) vuông tại M, có MI là đường trung tuyến ứng với cạnh huyền BC
\(\Rightarrow IM=IB=IC=\dfrac{BC}{2}\) (1)
\(\Delta BNC\) vuông tại N, có NI là đường trung tuyến ứng với cạnh huyền BC
\(\Rightarrow IN=IB=IC=\dfrac{BC}{2}\) (2)
Từ (1) và (2) \(\Rightarrow IM=IN=IB=IC=\dfrac{BC}{2}\)
Vậy \(I\) là tâm của đường tròn ngoại tiếp tứ giác BNMC
b) Do BNMC là tứ giác nội tiếp (cmt)
\(\Rightarrow\widehat{AMN}=\widehat{ABC}\) (góc ngoài tại đỉnh M bằng góc trong tại đỉnh B của tứ giác BNMC)
Xét \(\Delta AMN\) và \(\Delta ABC\) có:
\(\widehat{A}\) chung
\(\widehat{AMN}=\widehat{ABC}\) (cmt)
\(\Delta AMN\) ∽ \(\Delta ABC\) (g-g)
a: Xét tứ giác BNMC có \(\widehat{BNC}=\widehat{BMC}=90^0\)
nên BNMC là tứ giác nội tiếp đường tròn đường kính BC
tâm I là trung điểm của BC
b: Ta có: BNMC là tứ giác nội tiếp
=>\(\widehat{BNM}+\widehat{BCM}=180^0\)
mà \(\widehat{BNM}+\widehat{ANM}=180^0\)(hai góc kề bù)
nên \(\widehat{ANM}=\widehat{ACB}\)
Xét ΔANM và ΔACB có
\(\widehat{ANM}=\widehat{ACB}\)
\(\widehat{NAM}\) chung
Do đó: ΔANM~ΔACB