Tìm x, biết:
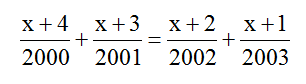
Cứu mik vs mai phải nộp rùi!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(-\dfrac{19}{49}=\dfrac{-19\cdot47}{49\cdot47}=\dfrac{-893}{2303}\)
\(\dfrac{-23}{47}=\dfrac{-23\cdot49}{47\cdot49}=\dfrac{-1127}{2303}\)
mà -893>-1127
nên \(-\dfrac{19}{49}>-\dfrac{23}{47}\)
b: \(\dfrac{-5}{8}=\dfrac{-5\cdot5}{8\cdot5}=\dfrac{-25}{40}\)
\(\dfrac{7}{-10}=\dfrac{-7}{10}=\dfrac{-7\cdot4}{10\cdot4}=\dfrac{-28}{40}\)
mà -25>-28
nên \(-\dfrac{5}{8}>\dfrac{7}{-10}\)
c: \(\dfrac{24}{35}=\dfrac{24\cdot6}{35\cdot6}=\dfrac{144}{210};\dfrac{19}{30}=\dfrac{19\cdot7}{30\cdot7}=\dfrac{133}{210}\)
mà 144>133
nên \(\dfrac{24}{35}>\dfrac{19}{30}\)

a: \(-\dfrac{15}{21}=\dfrac{-15:3}{21:3}=\dfrac{-5}{7}=\dfrac{-5\cdot11}{7\cdot11}=\dfrac{-55}{77}\)
\(\dfrac{-36}{44}=\dfrac{-36:4}{44:4}=\dfrac{-9}{11}=\dfrac{-9\cdot7}{11\cdot7}=\dfrac{-63}{77}\)
mà -55>-63
nên \(-\dfrac{15}{21}>-\dfrac{36}{44}\)
b: \(-\dfrac{16}{30}=\dfrac{-16:2}{30:2}=\dfrac{-8}{15}=\dfrac{-8\cdot4}{15\cdot4}=\dfrac{-32}{60}\)
\(\dfrac{-35}{84}=\dfrac{-35:7}{84:7}=\dfrac{-5}{12}=\dfrac{-5\cdot5}{12\cdot5}=\dfrac{-25}{60}\)
mà -32<-25
nên \(-\dfrac{16}{30}< -\dfrac{35}{84}\)
c: \(\dfrac{-5}{91}=\dfrac{-5\cdot101}{91\cdot101}=\dfrac{-505}{9191}\)
mà -505<-501
nên \(-\dfrac{5}{91}< -\dfrac{501}{9191}\)
a) Rút gọn:
\(-\dfrac{15}{21}=-\dfrac{15:3}{21:3}=-\dfrac{5}{7}\)
\(-\dfrac{36}{44}=-\dfrac{36:4}{44:4}=-\dfrac{9}{11}\)
Quy đồng(MSC:77)
\(-\dfrac{5}{7}=-\dfrac{5.11}{7.11}=-\dfrac{55}{77}\\ -\dfrac{9}{11}=-\dfrac{9.7}{11.7}=-\dfrac{63}{77}\)
Nhận thấy: \(-\dfrac{55}{77}>-\dfrac{63}{77}\Rightarrow-\dfrac{15}{21}>-\dfrac{36}{44}\)
b) Rút gọn:
\(-\dfrac{16}{30}=-\dfrac{16:2}{30:2}=-\dfrac{8}{15}\\ -\dfrac{35}{84}=-\dfrac{35:7}{84:7}=-\dfrac{5}{12}\)
Quy đồng (MSC:60)
\(-\dfrac{8}{15}=-\dfrac{8.4}{15.4}=-\dfrac{32}{60}\\ -\dfrac{5}{12}=-\dfrac{5.5}{12.5}=-\dfrac{25}{60}\)
Nhận thấy: \(-\dfrac{32}{60}< -\dfrac{25}{60}\Rightarrow-\dfrac{16}{30}< -\dfrac{35}{84}\)
c) \(-\dfrac{5}{91}=-\dfrac{5.101}{91.101}=-\dfrac{505}{9191}< -\dfrac{501}{9191}\)

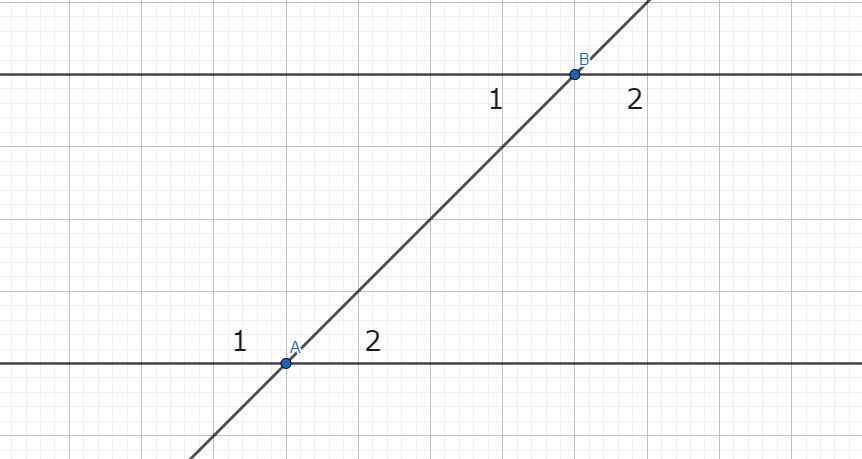 Ta có: \(\widehat{A_1}=\widehat{B_2}\) (theo giả thiết)
Ta có: \(\widehat{A_1}=\widehat{B_2}\) (theo giả thiết)
Mặt khác:
\(\left\{{}\begin{matrix}\widehat{A_1}+\widehat{A_2}=180^o\\\widehat{B_1}+\widehat{B_2}=180^o\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{A_1}=180^o-\widehat{A_2}\\\widehat{B_2}=180^o-\widehat{B_1}\end{matrix}\right.\) (hai cặp góc kề bù)
Mà \(\widehat{A_1}=\widehat{B_2}\) nên:
\(\widehat{A_2}=\widehat{B_1}\) Vậy nếu 1 đường thẳng cắt 2 đường thẳng mà trong các góc tạo thành có 1 cặp góc so le trong bằng nhau thì các cặp góc so le trong còn lại cũng bằng nhau.
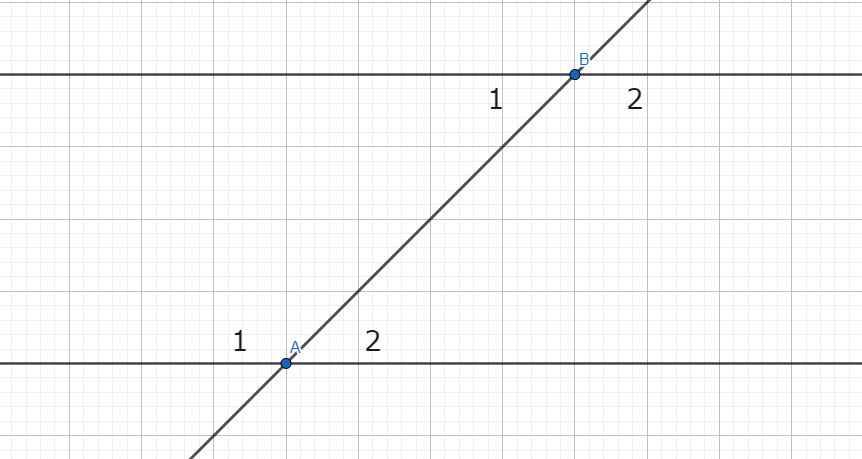 Giả sử \(\widehat{A_1}\) và \(\widehat{B_2}\) là cặp góc so le trong đề bài cho.
Giả sử \(\widehat{A_1}\) và \(\widehat{B_2}\) là cặp góc so le trong đề bài cho.
Ta có: \(\widehat{A_1}=\widehat{B_2}\) (theo giả thiết)
Mặt khác:
\(\left\{{}\begin{matrix}\widehat{A_1}+\widehat{A_2}=180^o\\\widehat{B_1}+\widehat{B_2}=180^o\end{matrix}\right.\)(hai cặp góc kề bù)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{A_1}=180^o-\widehat{A_2}\\\widehat{B_2}=180^o-\widehat{B_1}\end{matrix}\right.\)
Mà \(\widehat{A_1}=\widehat{B_2}\) nên:
\(\widehat{A_2}=\widehat{B_1}\) hay cặp góc so le trong còn lại bằng nhau
Vậy nếu 1 đường thẳng cắt 2 đường thẳng mà trong các góc tạo thành có 1 cặp góc so le trong bằng nhau thì cặp góc so le trong còn lại cũng bằng nhau.

1. Xét tam giác ABC vuông tại A:
2. Xét tam giác AHC vuông tại H:
3. Từ (1) và (2) suy ra:
4. Gọi I là giao điểm của tia phân giác góc ABC và tia phân giác góc CAH:
5. Xét tam giác ABI:
=> Góc BIA = 90 độ
6. Kết luận:
Vậy, tia phân giác của góc ABC và góc CAH vuông góc với nhau.

a) Với x thuộc Z, hiển nhiên cả tử và mẫu đều nguyên
Để A là số hữu tỉ thì:
\(x-1\ne0\Rightarrow x\ne1\)
Vậy để A là số hữu tỉ thì x nguyên và x khác 1
b) Để A là số hữu tỉ dương thì A là số hữu tỉ và A dương
A là số hữu tỉ câu a đã chứng minh
Xét A dương:
\(A=\dfrac{x+1}{x-1}>0\)
=>( x+1>0 và x-1>0 ) hoặc ( x+1<0 và x-1<0 )
=> (x>-1 và x>1) hoặc (x<-1 và x<1)
=> x>1 hoặc x<-1
Kết hợp ĐK A là số hữu tỉ thì x khác 1, x nguyên
Kết luận: x>1 hoặc x<-1, x nguyên thì A là số hữu tỉ dương
hoặc x thuộc Z, x khác {1;0;-1} thì A là số hữu tỉ dương
c) Để A là số hữu tỉ âm thì A là số hữu tỉ và A âm
Xét A âm:
\(A=\dfrac{x+1}{x-1}< 0\)
=> (x+1>0 và x-1<0) hoặc (x+1<0 và x-1>0)
=> (x>-1 và x<1) hoặc (x<-1 và x>1 : Vô lí )
=> -1<x<1
Kết hợp ĐK để A là số hữu tỉ thì: x nguyên và x khác 1
Kết luận: -1<x<1, x nguyên thì A là số hữu tỉ âm
Hay x = 0 thì A là số hữu tỉ âm
d) \(A=\dfrac{x+1}{x-1}=\dfrac{x-1+2}{x-1}=1+\dfrac{2}{x-1}\left(x\in Z,x\ne1\right)\)
Để A là số nguyên thì: 2/x-1 nguyên
=> 2 chia hết cho (x-1)
=> x-1 thuộc Ư(2)={1;-1;2;-2}
Bảng giá trị:
| x-1 | 1 | -1 | 2 | -2 |
| x | 2 | 0 | 3 | -1 |
| A | 3(nhận) | -1(loại) | 2(nhận) | 0(loại) |
Vậy x thuộc {2;3} thì A là số nguyên dương
\(\frac{x+4}{2000}+\frac{x+3}{2001}=\frac{x+2}{2002}+\frac{x+1}{2003}\\\Leftrightarrow \frac{x+4}{2000}+\frac{x+3}{2001}-\frac{x+2}{2002}-\frac{x+1}{2003}=0\\\Leftrightarrow \left(\frac{x+4}{2000}+1\right)+\left(\frac{x+3}{2001}+1\right)-\left(\frac{x+2}{2002}+1\right)-\left(\frac{x+1}{2003}+1\right)=0\\\Leftrightarrow \frac{x+2004}{2000}+\frac{x+2004}{2001}-\frac{x+2004}{2002}-\frac{x+2004}{2003}=0\\\Leftrightarrow (x+2024)\left(\frac{1}{2000}+\frac{1}{2001}-\frac{1}{2002}-\frac{1}{2003}\right)=0\\\Leftrightarrow x+2024=0(\text{vì }\frac{1}{2000}+\frac{1}{2001}-\frac{1}{2002}-\frac{1}{2003} \ne0)\\\Leftrightarrow x=-2024\)
Vậy phương trình có 1 nghiệm duy nhất là $x=-2024$.