`x + 5/6 = 4/3 `

`=> x = 4/3 - 5/6`

`=> x = 8/6 - 5/6`

`=> x = 3/6`

`=> x = 1/2`

Vậy ...

`x : 2^4 = 8^3`

`=> x : 2^4 = 2^9`

`=> x = 2^9 . 2^4`

`=> x = 2^13`

Vậy ...

`13/4 : (5/52 - x ) = 1/4`

`=> 5/52 - x = 13/4 : 1/4`

`=> 5/52 - x = 13`

`=> x = 5/52 - 13`

`=> x = -671/52`

Vậy ...

`a) x+5/6=4/3`

`x=4/3- 5/6`

`x=1/2`

`b) x: 2^4= 8^3`

`x:2^4= 2^9`

`x=2^9. 2^4`

`x=2^13`

`c) 13/4.(5/52 -  x)=1/4`

`(5/52-x)=13/4: 1/4`

`5/52 -x= 13`

`x=5/52- 13`

`x= -671/52`

không có tập nào

2\(x\) = 3y = 5Z ⇒ \(x=\dfrac{3}{2}y;z=\dfrac{3}{5}y\)

Thay \(x=\dfrac{3}{2}y\); z = \(\dfrac{3}{5}y\) vào biểu thức |\(x+y-z\)| = 95

ta có: |\(\dfrac{3}{2}y\) + y - \(\dfrac{3}{5}\)y| = 95

         |\(\dfrac{15}{10}y+\dfrac{10}{10}y-\dfrac{6}{10}y\)| = 95

          |\(\dfrac{25}{10}y-\dfrac{6}{10}y\)| = 95

          |\(\dfrac{19}{10}y\)| = 95

           \(\dfrac{19}{10}\).|y| = 95

            |y| = 95 : \(\dfrac{19}{10}\)

            |y| = 50

            \(\left[{}\begin{matrix}y=-50\\y=50\end{matrix}\right.\)

\(x=\dfrac{3}{2}.50\) = 75; z = \(\dfrac{3}{5}.50=30\) 

Vậy (\(x;y;z\)) = (75; 50; 30)

   Thay mặt thầy cô giáo cũng như tập thể đội ngũ những người đang hoạt động trong lĩnh vực giáo dục cảm ơn những lời chúc và những tình cảm tốt đẹp mà em đã giành cho thầy cô nói chung và Olm nói riêng. Chúc em luôn mạnh khỏe, an nhiên, bình yên trong cuộc  sống, nỗ lực và cố gắng học tập để trở thành những chủ nhân tương lai đất nước tài đức vẹn toàn. 

20-11 các cô sống hạnh phúc và mạnh khỏe ạaaa

A = \(\dfrac{5x-2}{x+2}\) (\(x\ne\) - 2;  0 ≤ \(x\in\)  Z)

A = \(\dfrac{5x-2}{x+2}\) \(\in\) Z ⇔ 5\(x\) - 2 ⋮ \(x+2\) 

          5\(x\) + 10 - 12 ⋮ \(x+2\)

          5(\(x+2\)) - 12 ⋮ \(x+2\)

                12 \(⋮\) \(x+2\) 

            \(x+2\) \(\in\) Ư(12) = {-12; - 6; -4; -3; -2; -1; 1; 2; 3; 4; 6; 12}

             \(x\) \(\in\) {-14; -8; -6; - 5; -4; -3; -1; 0; 1; 2; 4; 10}

   Vì 0≤ \(x\) \(\in\) Z nên \(x\) \(\in\) {0; 1; 2; 4; 10}

Vậy \(x\) \(\in\) {0; 1; 2; 4; 10}

\(x-y=-3\Leftrightarrow x+3=y\)

\(P=x^2\left(x+3\right)+y^2-x^2y-xy+x-4y+2003=\)

\(=x^2y+y^2-x^2y-xy+x-4y+2023=\)

\(=y^2-xy-3y+x-y+2023=\)

\(=y^2-y\left(x+3\right)+x-y+2003=\)

\(=y^2-y^2+\left(x-y\right)+2023=-3+2023=2000\)

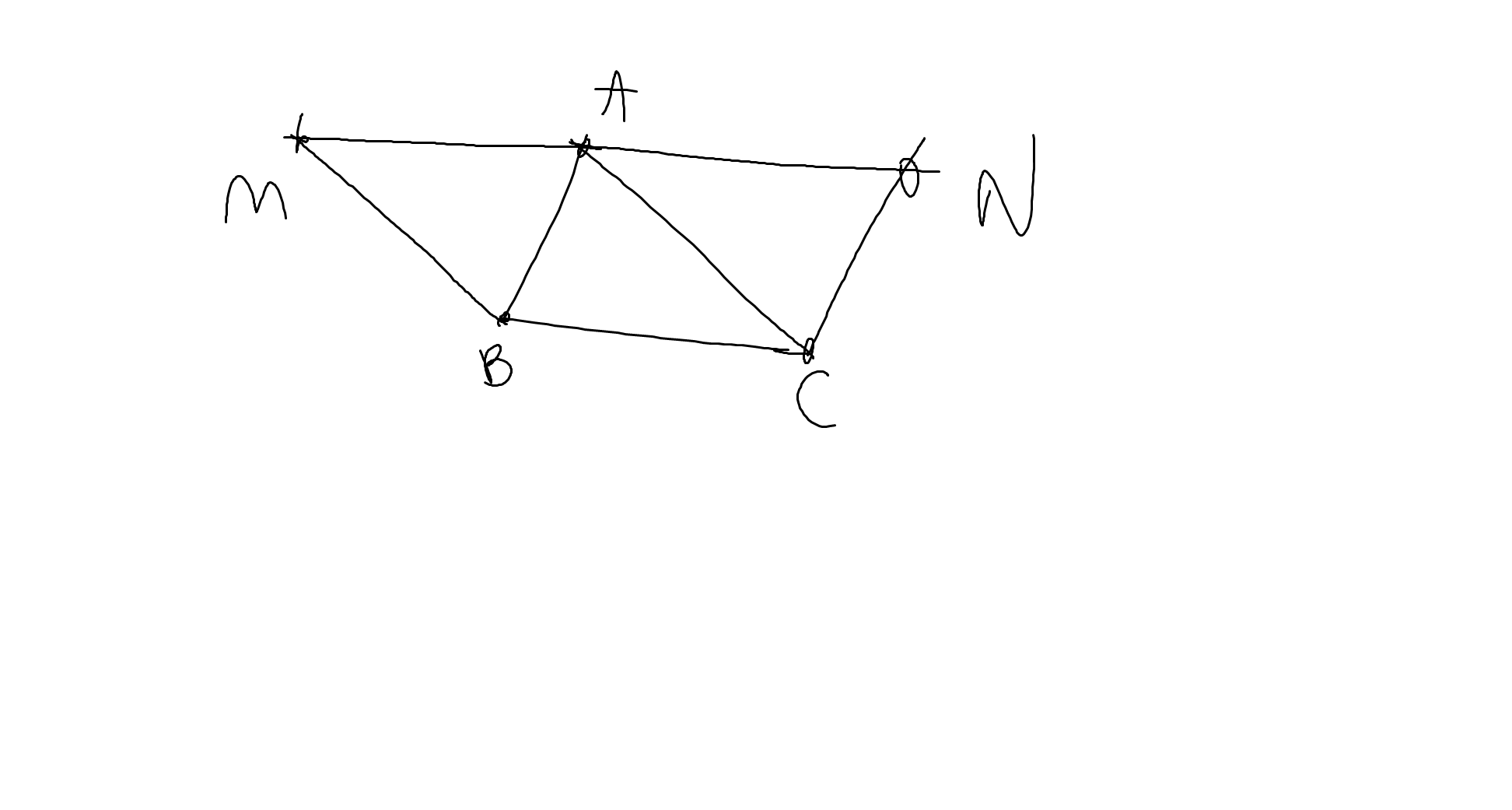
a: Xét ΔMAB và ΔCBA có

\(\widehat{MAB}=\widehat{ABC}\)(hai góc so le trong, MA//BC)

AB chung

\(\widehat{ABM}=\widehat{BAC}\)(hai góc so le trong, MB//AC)

Do đó;ΔMAB=ΔCBA

Xét ΔABC và ΔCNA có 

\(\widehat{BAC}=\widehat{NCA}\)(hai góc so le trong, BA//CN)

AC chung

\(\widehat{BCA}=\widehat{NAC}\)(hai góc so le trong, AN//BC)

Do đó: ΔABC=ΔCNA

b: ΔMAB=ΔCBA

=>MA=CB

ΔABC=ΔCNA

=>BC=NA

mà BC=AM

nên AM=AN

mà M,A,N thẳng hàng

nên A là trung điểm của MN

 Bài 3:

a: \(2^x+2^{x+1}+...+2^{x+100}=2^{101}-1\)

=>\(2^x\left(1+2+...+2^{100}\right)=2^{101}-1\)

Đặt \(A=1+2+...+2^{100}\)

=>\(2A=2+2^2+...+2^{101}\)

=>\(2A-A=2+2^2+...+2^{101}-1-2-...-2^{100}\)

=>\(A=2^{101}-1\)

\(2^x\left(1+2+...+2^{100}\right)=2^{101}-1\)

=>\(2^x\left(2^{101}-1\right)=2^{101}-1\)

=>\(2^x=1=2^0\)

=>x=0

b: p là số nguyên tố lớn hơn 3 nên \(\left\{{}\begin{matrix}p⋮̸2\\p⋮̸3\end{matrix}\right.\)

p không chia hết cho 3 nên p=3k+1 hoặc p=3k+2

TH3: p=3k+1

\(\left(p-1\right)\left(p+1\right)\)

\(=\left(3k+1-1\right)\left(3k+1+1\right)\)

\(=3k\left(3k+2\right)⋮3\)(3)

TH2: p=3k+2

\(\left(p-1\right)\left(p+1\right)=\left(3k+2-1\right)\left(3k+2+1\right)\)

\(=\left(3k+1\right)\left(3k+3\right)=3\left(k+1\right)\left(3k+1\right)⋮3\)(2)

Từ (2),(3) suy ra \(\left(p-1\right)\left(p+1\right)⋮3\)

p không chia hết cho 2 nên p=2k+1

\(\left(p-1\right)\left(p+1\right)=\left(2k+1-1\right)\left(2k+1+1\right)\)

\(=2k\left(2k+2\right)=4k\left(k+1\right)\)

Vì k;k+1 là hai số nguyên liên tiếp

nên \(k\left(k+1\right)⋮2\)

=>\(4k\left(k+1\right)⋮4\cdot2\)

=>\(4k\left(k+1\right)⋮8\)

=>\(\left(p-1\right)\left(p+1\right)⋮8\)

mà \(\left(p-1\right)\left(p+1\right)⋮3\)

và ƯCLN(3;8)=1

nên \(\left(p-1\right)\left(p+1\right)⋮3\cdot8=24\)