\(x^2\)-25-\(4xy\)\(+4y^2\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,27x^3-1\\ =\left(3x^3\right)-1^3\\ =\left(3x-1\right)\left(9x^2+3x+1\right)\\ \)
Sửa:
\(b,8x^3+27\\ =\left(2x\right)^3+3^3\\ =\left(2x+3\right)\left(4x^2-6x+9\right)\)
a: \(27x^3-1=\left(3x\right)^3-1^3\)
\(=\left(3x-1\right)\left[\left(3x\right)^2+3x\cdot1+1^2\right]\)
\(=\left(3x-1\right)\left(9x^2+3x+1\right)\)
b: Sửa đề: \(8x^3+27\)
\(8x^3+27=\left(2x\right)^3+3^3\)
\(=\left(2x+3\right)\left[\left(2x\right)^2-2x\cdot3+3^2\right]\)
\(=\left(2x+3\right)\left(4x^2-6x+9\right)\)

A B C D H E
Trên tia đối của AB lấy E sao cho AE=DC
Ta có DC//AB => DC//AE
=> AEDC là hình bình hành (Tứ giác có cặp cạnh đối // và = nhau là hbh)
Do ABCD là hình thang cân
\(\Rightarrow\widehat{BCD}=\widehat{ADC}\) (1)
Ta có AB//CD \(\Rightarrow\widehat{ADC}+\widehat{DAB}=180^o\) (2 góc trong cùng phí bù nhau) (2)
Mà \(\widehat{EAD}+\widehat{DAB}=\widehat{EAB}=180^o\) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{EAD}=\widehat{BCD}\)
Xét tg EAD và tg BCD có
AE = CD; \(\widehat{EAD}=\widehat{BCD}\left(cmt\right)\); AD = BC (gt)
=> tg EAD = tg BCD (c.g.c) => ED=BD => tg BDE cân tại D
Dựng \(DH\perp AB\left(H\in AB\right)\Rightarrow BH=EH=\dfrac{BE}{2}\) (trong tg cân đường cao hạ từ đỉnh tg cân đồng thời là đường trung tuyến)
Ta có
AE=CD \(\Rightarrow AB+CD=AB+AE=BE\)
\(DH=\dfrac{1}{2}\left(AB+CD\right)=\dfrac{1}{2}\left(AB+AE\right)=\dfrac{BE}{2}\)
\(\Rightarrow DH=BH=EH=\dfrac{BE}{2}\)
=> tg DHE và tg BHD là tg vuông cân tại H
\(\Rightarrow\widehat{DEH}=\widehat{EDH}=\widehat{BDH}=\widehat{DBH}=45^o\)
\(\Rightarrow\widehat{EDH}+\widehat{BDH}=\widehat{BDE}=45^o+45^o=90^o\Rightarrow ED\perp BD\)
Ta có
ED//AC (cạnh đối hbh AEDC)
\(\Rightarrow AC\perp BD\)

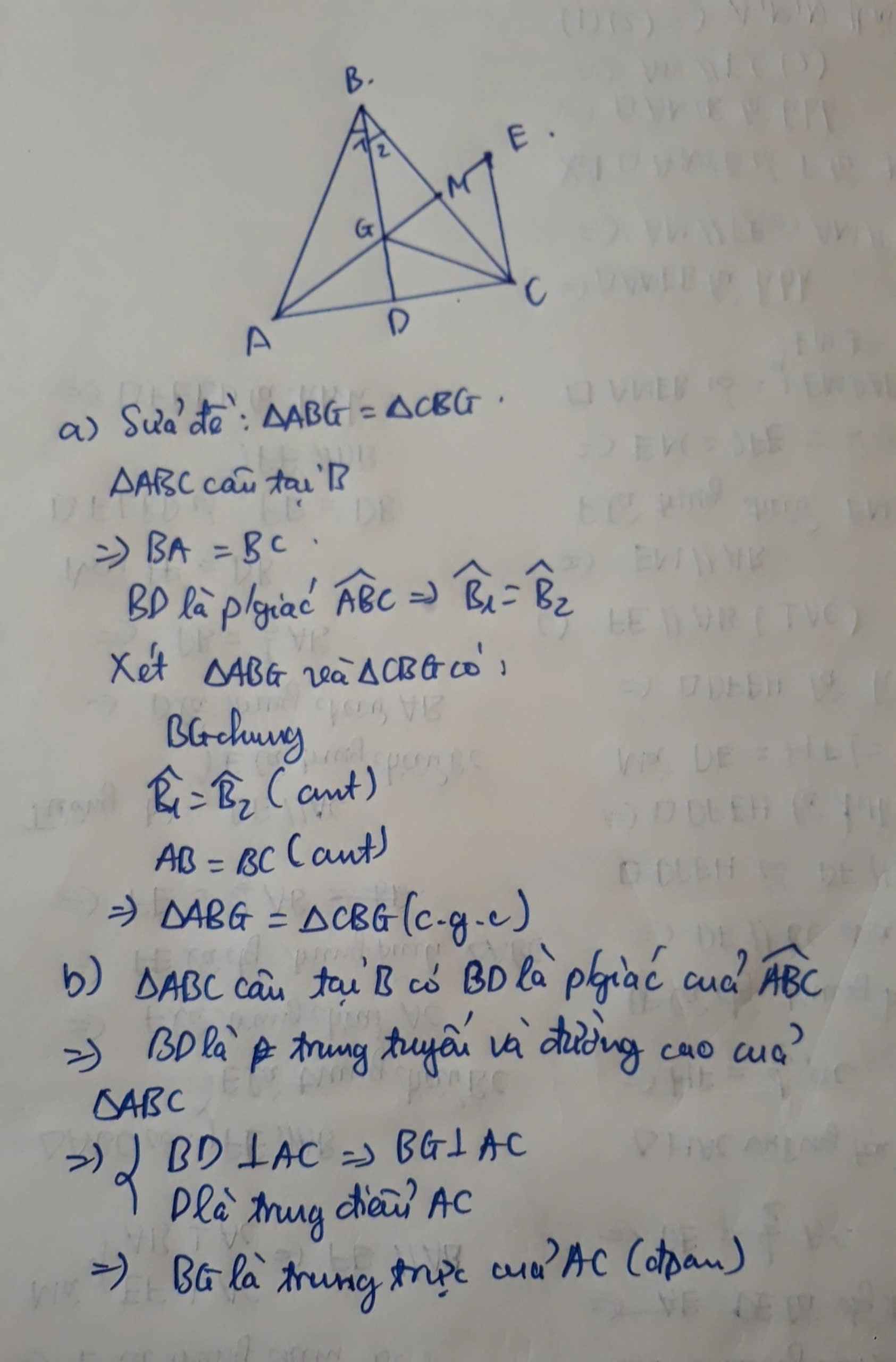
a: Xét ΔBAG và ΔBCG có
BA=BC
\(\widehat{ABG}=\widehat{CBG}\)
BG chung
Do đó: ΔBAG=ΔBCG
=>GA=GC
=>ΔGAC cân tại G
b: Ta có: BA=BC
=>B nằm trên đường trung trực của AC(1)
Ta có: GA=GC
=>G nằm trên đường trung trực của AC(2)
Từ (1),(2) suy ra BG là đường trung trực của AC

a: \(Q=\left(x-y\right)^2-\left(x-y\right)\left(x+y\right)+\left(x-2y\right)^2\)
\(=\left(x-y\right)\left(x-y-x-y\right)+\left(x-2y\right)^2\)
\(=-2y\left(x-y\right)+x^2-4xy+4y^2\)
\(=-2xy+2y^2+x^2-4xy+4y^2\)
\(=x^2-6xy+6y^2\)
b: \(\left(3x-1\right)^2-\left(x+7\right)^2-\left(2x-5\right)\left(2x+5\right)\)
\(=9x^2-6x+1-x^2-14x-49-\left(4x^2-25\right)\)
\(=8x^2-20x-48-4x^2+25=4x^2-20x-23\)

\(a,y^2+2y+1=y^2+2.y.1+1^2=\left(y+1\right)^2\)
\(b,9x^2+y^2-6xy=\left(3x\right)^2-2\cdot3x\cdot y+y^2=\left(3x-y\right)^2\)
\(c,25a^2+4b^2+20ab=\left(5a\right)^2+2\cdot5a\cdot2b+\left(2b\right)^2=\left(5a+2b\right)^2\)
\(d,x^2-x+\dfrac{1}{4}=x^2-2\cdot x\cdot\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2=\left(x-\dfrac{1}{2}\right)^2\)
`y^2 + 2y + 1 = y^2 + 2y .1 + 1^2 + (y+1)^2`
`9x^2 + y^2 - 6xy = (3x)^2 - 2.3x.y + y^2 = (3x + y)^2`
`25a^2 + 4b^2 + 20ab = (5a)^2 + 2.5a .2b + (2b)^2 = (5a + 2b)^2`
`x^2 - x + 1/4 = x^2 - 2x .1/2 +(1/2)^2 = (x-1/2)^2`

a: \(\dfrac{x-x^2}{5x^2-5}=\dfrac{x}{M}\)
=>\(M=\dfrac{x\left(5x^2-5\right)}{-x^2+x}=\dfrac{5x\left(x-1\right)\left(x+1\right)}{-x\left(x-1\right)}=-5\left(x+1\right)\)
=>M=-5x-5
b: \(\dfrac{x^2+8}{2x-1}=\dfrac{3x^3+24x}{M}\)
=>\(M=\dfrac{\left(2x-1\right)\left(3x^3+24x\right)}{x^2+8}=\dfrac{\left(2x-1\right)\cdot3x\left(x^2+8\right)}{\left(x^2+8\right)}\)
=>\(M=3x\left(2x-1\right)=6x^2-3x\)
c: \(\dfrac{M}{x-y}=\dfrac{3x^2-3xy}{3\left(y-x\right)^2}\)
=>\(\dfrac{M}{x-y}=\dfrac{3x\left(x-y\right)}{3\left(x-y\right)^2}=\dfrac{x}{x-y}\)
=>M=x

\(x^4+8x=0\)
=>\(x\left(x^3+8\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x^3+8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
\(x^4\) + 8\(x\) = 0
\(x^{ }\)(\(x^3\) + 8) = 0
\(\left[{}\begin{matrix}x=0\\x^3+8=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x^3=-8\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
Vậy \(x\) \(\in\) {-2; 0}

ΔAED vuông tại A
=>\(AE^2+AD^2=ED^2\)
ΔAEB vuông tại A
=>\(AE^2+AB^2=EB^2\)
ΔACD vuông tại A
=>\(AC^2+AD^2=CD^2\)
ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
\(CD^2-CB^2=CA^2+AD^2-CA^2-AB^2=AD^2-AB^2\)
\(ED^2-EB^2=AE^2+AD^2-AE^2-AB^2=AD^2-AB^2\)
Do đó: \(CD^2-CB^2=ED^2-EB^2\)
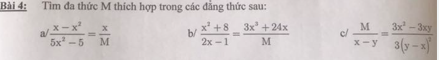
(\(x^2\) - 4\(xy\) + 4y2) - 25
= (\(x\) - 2y)2 - 25
= (\(x-2y\) - 5)(\(x-2y\) + 5)