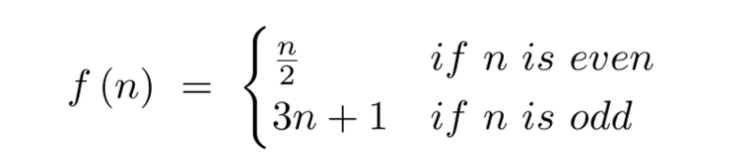Chứng minh rằng phép vị tự biến mỗi đường thẳng thành một đường thẳng song song hoặc trùng với nó, biến mỗi mặt phẳng thành một mặt phẳng song song hoặc trùng với mặt phẳng đó.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đề thi đánh giá năng lực
NT
3
NT
21 tháng 12 2023
Bố của Nam sinh năm 1980. Năm đó thuộc thế kỉ nào?
Nhanh nhẹn lên.
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
20 tháng 12 2023
A B C H D E K I
a/
Ta có
\(AB\perp AC\Rightarrow AD\perp AC;HE\perp AC\) => AD//HE
\(AC\perp AB\Rightarrow AE\perp AB,HD\perp AB\) => AE//HD
=> ADHE là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Mà \(\widehat{A}=90^o\)
=> ADHE là hình CN
b/
Xét tg vuông ADH có
\(DH=\sqrt{AH^2-AD^2}\) (Pitago)
\(\Rightarrow DH=\sqrt{5^2-4^2}=3cm\)
\(\Rightarrow S_{ADHE}=AD.DH=4.3=12cm^2\)
c/
Ta có
DB=DI (gt); DH=DK (gt) => BKIH là hbh (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
Xét tg AKH có
\(HD\perp AB\Rightarrow AD\perp HK\) (1)
BKIH là hình bình hành (cmt) => KI//BH (cạn đối hbh)
Mà \(AH\perp BC\left(gt\right)\Rightarrow BH\perp AH\)
\(\Rightarrow KI\perp AH\) (2)
Từ (1) và (2) => I là trực tâm của tg AKH => \(AK\perp HI\) (trong tg 3 đường cao đồng quy)
NH
1
18 tháng 12 2023
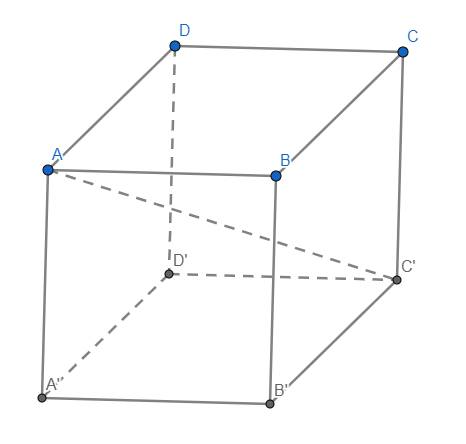
Ta có \(3AB^2=AC'^2=9a^2\) \(\Leftrightarrow AB^2=3a^2\Leftrightarrow AB=a\sqrt{3}\)
\(\Rightarrow V_{hlp}=AB^3=3a^3\sqrt{3}\) (đơn vị thể tích)
DN
1
TN
31 tháng 12 2023
tại con bò này đứng lên con bò kia = 2 chân theo hình vòng tròn và không đếm chân ông đếm :)))
mình lớp 7
NN
0
