Cho hình bình hành ABCD, hai đường chéo cắt nhau tại O. E thuộc OB và F thuộc OD sao cho BE = DF. Chứng minh AE // CF
mik cần gấp cm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: Xét ΔNAI và ΔNCK có
\(\widehat{NAI}=\widehat{NCK}\)(AI//CK)
NA=NC
\(\widehat{ANI}=\widehat{CNK}\)(hai góc đối đỉnh)
Do đó: ΔNAI=ΔNCK
=>NI=NK
c: ΔAHB=ΔAHC
=>HB=HC
=>H là trung điểm của CB
Xét ΔABC có
AH,BN là các đường trung tuyến
AH cắt BN tại I
Do đó: I là trọng tâm của ΔABC
=>BI=2IN
mà IK=2IN
nên BI=IK
=>I là trung điểm của BK
Ta có: KC//AH
AH\(\perp\)BC
Do đó: KC\(\perp\)CB
=>ΔKCB vuông tại C
ΔCKB vuông tại C
mà CI là đường trung tuyến
nên IC=IK=IB
Xét ΔKBC có
KH,CI là các đường trung tuyến
KH cắt CI tại G
Do đó: G là trọng tâm của ΔKBC
=>IG=1/3IC
mà IC=IK
nên \(IG=\dfrac{1}{3}IK\)

Giải:
Vì a : 6 dư 2 ⇒ a + 10 ⋮ 6
a : 11 dư 1 ⇒ a + 10 ⋮ 11
⇒ a + 10 ⋮ 6 và 11
6 = 2.3; 11 = 11; BCNN(6; 11) = 2.3.11 = 66
⇒ a + 10 ⋮ 66
Vậy a chia 66 dư 10

Giải:
Nửa chu vi hình chữ nhật là: 54 x 2 = 108 (dm)
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Chiều rộng của thửa ruộng hình chữ nhật là:
108 : (3 + 5) x 3 = 40,5 (dm)
Chiều dài của thửa ruộng là:
108 - 40,5 = 67,5 (dm)
Diện tích thửa ruộng là:
67,5 x 40,5 = 2733,75 (dm2)
Đáp số:..
Chu vi miếng đất hình vuông là:
54 x 4 = 216 (dm)
Nửa chu vi thửa ruộng HCN là:
216 : 2 = 108 (dm)
Chiều rộng thửa ruộng HCN là:
108 : (3+5) x 3 = 40,5 (dm)
Chiều dài thửa ruộng HCN là:
108 - 40,5 = 67,5 (dm)
Diện tích thửa ruộng HCN là:
40,5 x 67,5 = 2733,75 (dm2)

Lời giải:
Vì $\overline{a25b}$ chia 5 dư 1 nên có tận cùng $(b)$ là 6 hoặc 1.
Vì $\overline{a25b}$ chia hết cho $2$ nên $b$ chẵn.
$\Rightarrow b=6$
$a$ có thể nhận bất cứ giá trị nào từ 1 đến 9.
Vậy số thỏa mãn là: $1256, 2256, 3256, 4256, 5256, 6256,7256,8256,9256$

a: Số học sinh toàn trường là:
60:15%=60:0,15=400(bạn)
b: Số học sinh khối 5 là:
400x22,5%=90(bạn)

a: Xét tứ giác AMHN có \(\widehat{AMH}+\widehat{ANH}=90^0+90^0=180^0\)
nên AMHN là tứ giác nội tiếp
b: Xét tứ giác BNMC có \(\widehat{BNC}=\widehat{BMC}=90^0\)
nên BNMC là tứ giác nội tiếp
=>\(\widehat{BNM}+\widehat{BCM}=180^0\)
mà \(\widehat{BNM}+\widehat{ANM}=180^0\)(hai góc kề bù)
nên \(\widehat{ANM}=\widehat{ACB}\)

Thay y=-2 vào (d), ta được:
\(\dfrac{1}{2}x+2=-2\)
=>\(\dfrac{x}{2}=-4\)
=>x=-8
Thay x=-8 và y=-2 vào y=ax+b, ta được:
\(a\cdot\left(-8\right)+b=-2\)
=>-8a+b=-2
=>8a-b=2(1)
Thay x=2 và y=-3 vào y=ax+b, ta được:
\(a\cdot2+b=-3\)
=>2a+b=-3(2)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}8a-b=2\\2a+b=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}10a=-1\\8a-b=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=-\dfrac{1}{10}\\b=8a-2=-\dfrac{8}{10}-2=-\dfrac{28}{10}=-\dfrac{14}{5}\end{matrix}\right.\)
Vậy: (d'): \(y=-\dfrac{1}{10}x-\dfrac{14}{5}\)

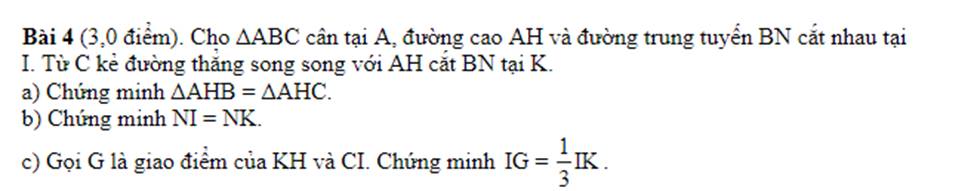

Xét tam giác AEB và tam giác CFD ta có
AB = CD (tứ giác ABCD là hbn); ^ABE = ^CDF ( soletrong ) ; DF = BE (gt)
Vậy tam giác AEB = tam giác CFD ( c.g.c )
=> AE = FC ( 2 cạnh tương ứng ) (1)
tương tự với tam giác AFD = tam giác EBC
=> AF = EC (2)
Từ (1) ; (2) => tứ giác AECF là hbh => AE // CF
Xét tam giác AEB và tam giác CFD ta có
AB = CD (tứ giác ABCD là hbn); ^ABE = ^CDF ( soletrong ) ; DF = BE (gt)
Vậy tam giác AEB = tam giác CFD ( c.g.c )
=> AE = FC ( 2 cạnh tương ứng ) (1)
tương tự với tam giác AFD = tam giác EBC
=> AF = EC (2)
Từ (1) ; (2) => tứ giác AECF là hbh => AE // CF