a: Xét ΔCAB vuông tại A và ΔCAD vuông tại A có

CA chung

AB=AD

Do đó: ΔCAB=ΔCAD

=>CB=CD

=>ΔBCD cân tại C

b: Xét ΔMCB và ΔMDE có

\(\widehat{MCB}=\widehat{MDE}\)(BC//DE)

MC=MD

\(\widehat{CMB}=\widehat{DME}\)(hai góc đối đỉnh)

Do đó: ΔMCB=ΔMDE

=>CB=DE

Xét ΔEDB có ED+DB>BE

mà ED=CB

nên BC+BD>BE

a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có

BD chung

\(\widehat{ABD}=\widehat{EBD}\)

Do đó: ΔBAD=ΔBED

b: ΔBAD=ΔBED

=>DA=DE

Xét ΔDAN vuông tại A và ΔDEC vuông tại E có

DA=DE

\(\widehat{ADN}=\widehat{EDC}\)(hai góc đối đỉnh)

Do đó: ΔDAN=ΔDEC

=>AN=EC

c: Xét ΔBNC có

NE,CA là các đường cao

NE cắt CA tại D

Do đó: D là trực tâm của ΔBNC

=>BD\(\perp\)NC

Đặt \(x^{2023}-16x^{2019}=0\)

=>\(x^{2019}\left(x^4-16\right)=0\)

=>\(\left[{}\begin{matrix}x^{2019}=0\\x^4-16=0\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x=0\\x^4=16\end{matrix}\right.\Leftrightarrow x\in\left\{0;2;-2\right\}\)

Hii, chào bạn nhé! Mình có thể giúp gì cho bạn ạ? Nếu bạn muốn biết nghĩa của từ hello thì đó có nghĩa là ''xin chào'' trong tiếng Việt và ''kon'nichiwa'' trong tiếng Nhật. Nếu bạn muốn dịch sang thứ tiếng khác, hãy hỏi mình nhé!

\(#CongChuaAnna\)

hi

a: Diện tích đáy là 4x4=16(cm)

Chiều cao là 64:16=4(cm)

b: Thể tích là: \(V=4^2\cdot4=64\left(cm^3\right)\)

                  Giải:

Gọi số tiền mà mẹ đưa An đóng tiền điện, tiền mước, tiền internet lần lượt là: \(x;y;z\)  (đồng); \(x;y;z\)  > 0

Theo bài ra ta có:

\(\dfrac{x}{7}=\dfrac{y}{5}=\dfrac{z}{2}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{x}{7}\) = \(\dfrac{y}{5}\) = \(\dfrac{z}{2}\) = \(\dfrac{x+y+z}{7+5+2}\) = \(\dfrac{5600000}{14}\) = 400 000

\(x\) = 400 000 x 7 = 2 800 000 

y = 400 000 x 5 = 2 000 000 

z = 400 000 x 2 = 800 000 

Vậy số tiền điện, nước, internet mà bạn An phải đóng lần lượt là:

   2 800 000 đồng; 2 000 000 đồng; 800 000 đồng.

`#3107.101107`

`x^3 - 4 = 0`

`\Rightarrow x^3 = 4`

`\Rightarrow x =`\(\sqrt[3]{4}\)

Vậy, \(x=\sqrt[3]{4}.\)

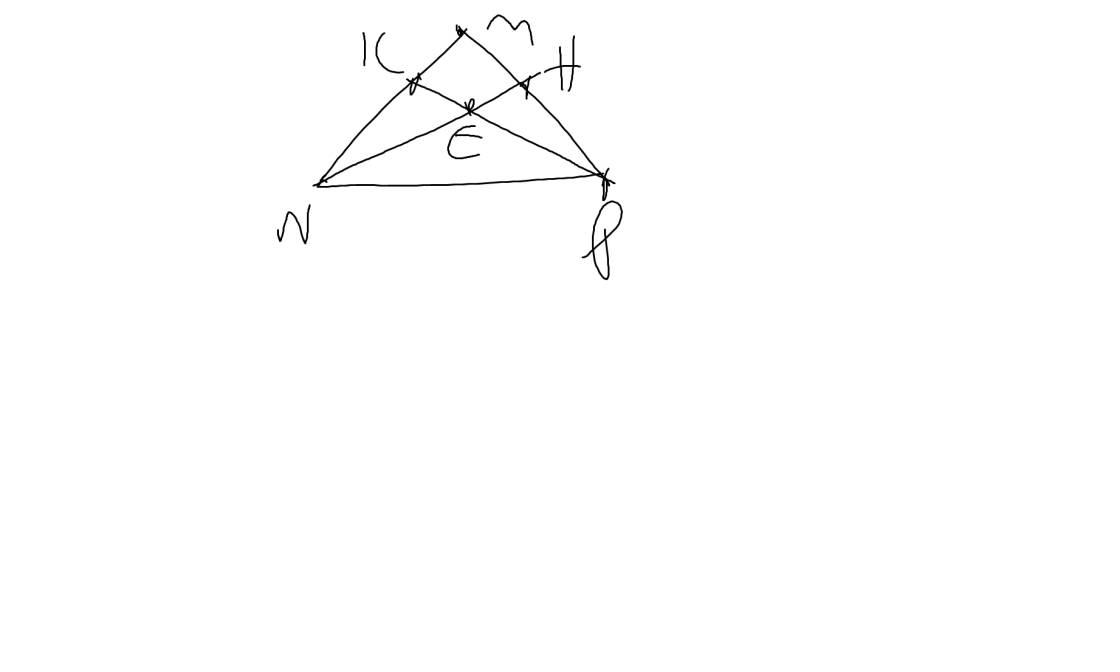
a: Xét ΔKNP vuông tại K và ΔHPN vuông tại H có

NP chung

\(\widehat{KNP}=\widehat{HPN}\)

Do đó: ΔKNP=ΔHPN

b: Xét ΔMNP có

NH,PK là các đường cao

NH cắt PK tại E

Do đó: E là trực tâm của ΔNMP

=>ME\(\perp\)NP

a: Xét ΔCAB vuông tại A và ΔCAD vuông tại A có

CA chung

AB=AD

Do đó: ΔCAB=ΔCAD

b: ΔCAB=ΔCAD

=>CB=CD
=>ΔCBD cân tại C
AB=AD

=>A là trung điểm của BD

=>\(BD=2\cdot AB=6\left(cm\right)\)

Chu vi tam giác CBD là:
CB+CD+BD

=2CB+2BA

=2(CB+BA)=2(5+3)=16(cm)

c: Xét ΔCDE vuông tại Dvà ΔCBE vuông tại B có

CE chung

CD=CB

Do đó: ΔCDE=ΔCBE

=>ED=EB

=>E nằm trên đường trung trực của DB(1)

Ta có: ΔCDB cân tại C

mà CA là đường cao

nên CA là đường trung trực của DB(2)

Từ (1),(2) suy ra C,A,E thẳng hàng