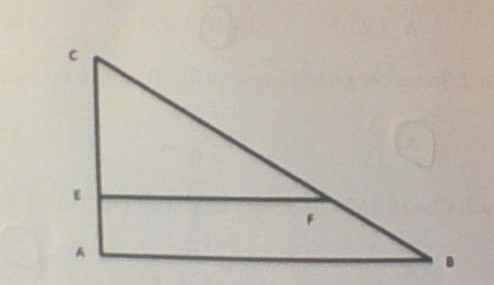
Cho tam giác ABC vuông ở A. Hai cạnh kề với góc vuông AC dài 12cm và AB dài 18cm. Điểm E nằm trên cạnh AC có AE = EC/ 2. Từ điểm E kẻ đường thẳng song song với AB cắt tại BC tại F.
a) Tính diện tích tam giác ABC.
b) Tính diện tích tam giác ABF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ψ(`∇´)ψ Like cái kìa !!!!
Đặt số ban đầu có hai chữ số là AB, với A và B lần lượt là chữ số hàng đơn vị và hàng đơn vị.
Theo yêu cầu của bài toán, số mới khi thêm chữ số 7 vào bên phải sẽ là AB7.
Ta có phương trình:
AB7 - AB = 565
Đổi số AB7 thành dạng toán học: 100A + 10B + 7
Kết hợp với phương trình ta có:
100A + 10B + 7 - (10A + B) = 565
100A + 10B + 7 - 10A - B = 565
90A + 9B + 7 = 565
90A + 9B = 558
10A + B = 62
Vì A và B đều là số tự nhiên từ 0 đến 9, ta thử các giá trị có thể của A và B:
- Thử A = 6, B = 2: 62 không lớn hơn 565 đơn vị, loại.
- Thử A = 5, B = 7: 57 không lớn hơn 565 đơn vị, loại.
- Thử A = 4, B = 7: 47 không lớn hơn 565 đơn vị, loại.
- Thử A = 3, B = 2: 32 không lớn hơn 565 đơn vị, loại.
- Thử A = 2, B = 7: 27 không lớn hơn 565 đơn vị, loại.
- Thử A = 1, B = 2: 12 không lớn hơn 565 đơn vị, loại.
Vậy giá trị của A và B là 7 và 1. Vậy số cần tìm là 71.

Số lượng phần tử: \(\dfrac{\left(2023-1\right)}{2}+1=1012\)
Số cặp là: \(\dfrac{1012}{2}\)
Kết quả biểu thức: \(\dfrac{1012}{2}\cdot2=1012\)
Chọn D

Số số hạng trong dãy là x-6+1=x-5(số)
Tổng của dãy số là (x+6)x(x-5):2
Theo đề, ta có:
\(\left(x+6\right)\times\dfrac{\left(x-5\right)}{2}=195\)
=>\(\left(x+6\right)\times\left(x-5\right)=390\)
=>\(x^2+x-420=0\)
=>(x+21)(x-20)=0
=>\(\left[{}\begin{matrix}x=-21\left(loại\right)\\x=20\left(nhận\right)\end{matrix}\right.\)
Vậy: x=20
\(6+7+8+9+...+x=195\)
\(1+2+3+...+x-\left(1+2+3+4+5\right)=195\)
\(\dfrac{x\left(x+1\right)}{2}-\left(1+2+3+4+5\right)=195\)
\(\dfrac{x\left(x+1\right)}{2}=210\)
\(x\left(x+1\right)=420\)
\(x\cdot x+x=420\)
\(x=420\)

Hiệu số tiền lãi 2 bên:
\(200000-90000=110000\left(đ\right)\)
Hiệu số tiền bán 2 bên:
\(40000-38000=2000\left(đ\right)\)
Chiều dài tấm vải:
\(\dfrac{110000}{2000}=55\left(m\right)\)
Đáp số: 55m

$7,36\times x+2,64\times x=8$
$x\times(7,36+2,64)=8$
$x\times10=8$
$x=8:10$
$x=0,8$
\(7,36\times x+2,64\times x=8\\ \left(7,36+2,64\right)\times x=8\\ 10\times x=8\\ x=8:10\\ x=0,8\)

36 × (x - 9) = 900
x - 9 = 900 : 36
x - 9 = 25
x = 25 + 9
x = 34

a: Chu vi hình chữ nhật ABCD là:
C=2x(AB+AD)=2x(40+24)=128(cm)
b: \(AK=\dfrac{AB}{4}=\dfrac{40}{4}=10\left(cm\right)\)
AK+BK=AB
=>BK+10=40
=>BK=30(cm)
Diện tích hình thang vuông DKBC là:
\(S_{DKBC}=\dfrac{1}{2}\times\left(BK+DC\right)\times DC=\dfrac{1}{2}\times\left(30+40\right)\times24\)
\(=12\times70=840\left(cm^2\right)\)
c: AK/DC=1/4
mà AK//DC
nên \(\dfrac{EA}{ED}=\dfrac{1}{4}\)
=>\(\dfrac{EA}{AD}=\dfrac{1}{3}\)
=>\(EA=\dfrac{AD}{3}=\dfrac{24}{3}=8\left(cm\right)\)
a: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\times AC\times AB=\dfrac{1}{2}\times12\times18=108\left(cm^2\right)\)
b: Vì AE=EC/2
nên \(EC=\dfrac{2}{3}\times AC\)
EF//AB
=>\(\dfrac{CF}{CB}=\dfrac{CE}{CA}=\dfrac{2}{3}\)
=>\(\dfrac{BF}{BC}=\dfrac{1}{3}\)
=>\(S_{ABF}=\dfrac{1}{3}\times S_{ABC}=\dfrac{1}{3}\times108=36\left(cm^2\right)\)