Bạn có thể ghi đề rõ ra không?

mình đag cần gấp bn có thể giúp luôn đc k

3x-10=2x+13

3x-2x=10+13

        x=23

Vậy x=23

Ta có :

3 × x - 10 = 2 × x + 13

=> 2 × x + 13 + 10 = 3 × x

Vậy x = 10 + 13 = 23

Tick cho mình nha

Lời giải:

$a^3+3a^2+5=5^b$

$\Rightarrow a^2(a+3)+5=5^b$

$\Rightarrow a^2.5^c+5=5^b$

$\Rightarrow 5(a^2.5^{c-1}+1-5^{b-1})=0$

$\Rightarrow a^2.5^{c-1}+1=5^{b-1}$

Nếu $b,c$ đều là số nguyên dương lớn hơn $1$ thì:

$1=5^{b-1}-a^2.5^{c-1}\vdots 5$ (vô lý)

Do đó trong 2 số $b,c$ tồn tại ít nhất 1 số nguyên dương bằng 1

Nếu $b=1$ thì:

$a^2.5^{c-1}+1=5^{1-1}=1\Rightarrow a^2.5^{c-1}=0$

$\Rightarrow a=0$ (không tm do $a$ nguyên dương)

Nếu $c=1$ thì $a+3=5^c=5\Rightarrow a=2$

$a^2.5^{c-1}+1=5^{b-1}$

$\Leftrightarrow a^2.5^{1-1}+1=5^{b-1}$

$\Leftrightarrow 2^2+1=5^{b-1}\Rightarrow b-1=1\Rightarrow b=2$

Vậy $(a,b,c)=(2,2,1)$

Gọi số cây lớp 7A,7B,7C trồng được lần lượt là a(cây),b(cây),c(cây)

(Điều kiện: \(a,b,c\in Z^+\))

Số cây lớp 7A;7B;7C trồng được lần lượt tỉ lệ thuận với 9;8;7

=>\(\dfrac{a}{9}=\dfrac{b}{8}=\dfrac{c}{7}\)

Lớp 7C trồng ít hơn lớp 7A 10 cây nên ta có: a-c=10

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{9}=\dfrac{b}{8}=\dfrac{c}{7}=\dfrac{a-c}{9-7}=\dfrac{10}{2}=5\)

=>\(a=5\cdot9=45;b=5\cdot8=40;c=5\cdot7=35\)

Vậy: số cây lớp 7A,7B,7C trồng được lần lượt là 45 cây; 40 cây; 35 cây

a: \(3x^3+ax^2+bx+9⋮x^2-9\)

=>\(3x^3-27x+ax^2-9a+\left(b+27\right)x+9a+9⋮x^2-9\)

=>\(\left\{{}\begin{matrix}b+27=0\\9a+9=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}b=-27\\a=-1\end{matrix}\right.\)

b: \(10n^2+n-10⋮n-1\)

=>\(10n^2-10n+11n-11+1⋮n-1\)

=>\(1⋮n-1\)

=>\(n-1\in\left\{1;-1\right\}\)

=>\(n\in\left\{2;0\right\}\)

làm sao để từ (b+27)x =>b+27=0 đc vứt luôn x đi ạ mình ko hiểu đoạn đó lắm ạ

a: M là trung điểm của BC

=>\(BM=CM=\dfrac{BC}{2}\)

mà BA=BC/2

nên BM=CM=BA

Xét ΔBAD và ΔBMD có

BA=BM

\(\widehat{ABD}=\widehat{MBD}\)

BD chung

Do đó: ΔBAD=ΔBMD

b: ta có; ΔBAD=ΔBMD

=>\(\widehat{BAD}=\widehat{BMD}\)

Xét ΔBAC và ΔBME có

\(\widehat{BAC}=\widehat{BME}\)

BA=BM

\(\widehat{ABC}\) chung

Do đó: ΔBAC=ΔBME

=>BE=BC

=>ΔBEC cân tại B

Ta có: ΔBEC cân tại B

mà BD là đường phân giác

nên DB là đường trung tuyến

=>N là trung điểm của EC

Xét ΔEBC có

BN,EM là các đường trung tuyến

BN cắt EM tại D

Do đó: D là trọng tâm của ΔEBC

=>BD/DN=2

Đồ thị hàm số đi qua A(- \(\dfrac{1}{2}\); 1)

⇔ m.|- \(\dfrac{1}{2}\)| + 2.(-\(\dfrac{1}{2}\)) = 1

     \(\dfrac{1}{2}\)m - 1 = 1

      \(\dfrac{1}{2}\)m = 2

          m = 2 x 2

         m = 4

Kết luận với m = 4 thì đồ thị hàm số đi qua A(- \(\dfrac{1}{2}\); 1)

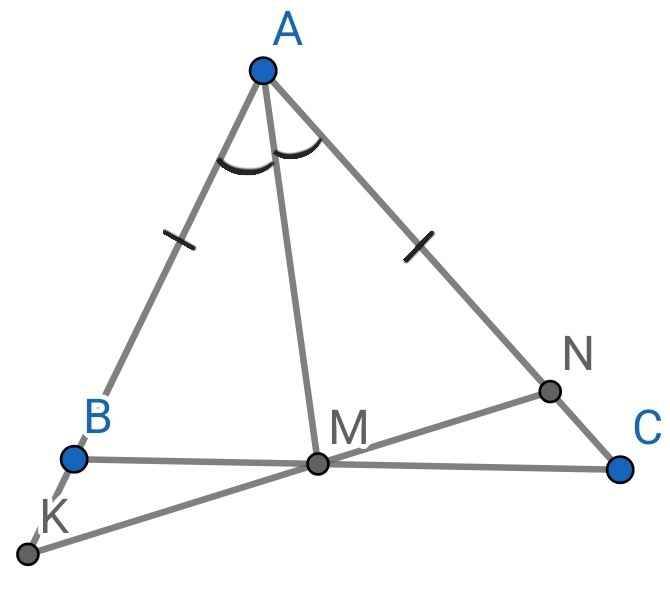
Do AM là tia phân giác của ∠BAC (gt)

⇒ ∠BAM = ∠CAM

⇒ ∠BAM = ∠NAM

Xét ∆ABM và ∆ANM có:

AB = AN (gt)

∠BAM = ∠NAM (cmt)

AM là cạnh chung

⇒ ∆ABM = ∆ANM (c-g-c)

⇒ MB = MN (hai cạnh tương ứng)

Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)

=>\(2\cdot\left(\widehat{IBC}+\widehat{ICB}\right)=180^0-65^0=115^0\)

=>\(\widehat{IBC}+\widehat{ICB}=57,5^0\)

Xét ΔIBC có \(\widehat{IBC}+\widehat{ICB}+\widehat{BIC}=180^0\)

=>\(\widehat{BIC}=180^0-57,5^0=122,5^0\)

a: Ta có: \(\widehat{ABD}=\dfrac{\widehat{ABC}}{2}\)

\(\widehat{ACE}=\dfrac{\widehat{ACB}}{2}\)

mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)

nên \(\widehat{ABD}=\widehat{ACE}\)

Xét ΔADB và ΔAEC có

\(\widehat{ABD}=\widehat{ACE}\)

AB=AC

\(\widehat{BAD}\) chung

Do đó: ΔADB=ΔAEC

=>BD=CE

b: Ta có: ΔADB=ΔAEC

=>AD=AE

=>ΔADE cân tại A

c: Xét ΔABC có \(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)

nên ED//BC