K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
13 tháng 4 2024
Sửa đề: \(\dfrac{1}{2}x+\dfrac{3}{2}\left(x-5\right)=3\)
=>\(\dfrac{1}{2}x+\dfrac{3}{2}x-\dfrac{15}{2}=3\)
=>\(2x=3+\dfrac{15}{2}=\dfrac{21}{2}\)
=>\(x=\dfrac{21}{2}:2=\dfrac{21}{4}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 4 2024
\(\dfrac{1}{2}\) x \(\dfrac{3}{2}\) x (\(x-5\)) = 3
\(x-5\) = 3 : (\(\dfrac{1}{2}\) x \(\dfrac{3}{2}\))
\(x-5\) = 4
\(x\) = 4 + 5
\(x\) = 9
Vậy \(x=9\)
13 tháng 4 2024
a: \(M\left(x\right)=2x^3-x^2+8x-1-3x^2\)
\(=2x^3+\left(-x^2-3x^2\right)+8x-1\)
\(=2x^3-4x^2+8x-1\)
\(N\left(x\right)=-4x^2+2x^2+3+5+7x\)
\(=\left(-4x^2+2x^2\right)+7x+8\)
\(=-2x^2+7x+8\)
b: M(x)+N(x)
\(=2x^3-4x^2+8x-1-2x^2+7x+8\)
\(=2x^3-6x^2+15x+7\)
c: \(3x^2\left(5x^2-x+2\right)\)
\(=3x^2\cdot5x^2-3x^2\cdot x+3x^2\cdot2\)
\(=15x^4-3x^3+6x^2\)
LT
2
13 tháng 4 2024
\(\dfrac{-2x^4-\dfrac{7}{2}x^3-17x^2+9x-7}{2-x}\)
\(=\dfrac{2x^4+3,5x^3+17x^2-9x+7}{x-2}\)
\(=\dfrac{2x^4-4x^3+7,5x^3-15x^2+32x^2-64x+55x-110+117}{x-2}\)
\(=2x^3+7,5x^2+32x+55+\dfrac{117}{x-2}\)
NH
1
12 tháng 4 2024
Bài 5:
a: Xét ΔABC có AB<AC
mà BH,CH lần lượt là hình chiếu của AB,AC trên BC
nên HB<HC
Xét ΔMBC có
HB<HC
mà HB,HC lần lượt là hình chiếu của MB,MC trên BC
nên MB<MC
b: Xét ΔBMH có \(\widehat{DMH}\) là góc ngoài tại M
nên \(\widehat{DMH}=\widehat{MHB}+\widehat{MBH}=90^0+\widehat{MBH}>90^0\)
Xét ΔDMH có \(\widehat{DMH}>90^0\)
nên DH là cạnh lớn nhất của ΔDMH
=>DH>DM
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
12 tháng 4 2024
a; Biểu thức biểu thị số tiền mua y vở và mua x bút là:
6000 x \(x\) + 8000 x y
b; Số tiền dự định mua 5 cái bút và 15 quyển vở là:
6000 x 5 + 8000 x 15 = 150 000 (đồng)
Kết luận:..
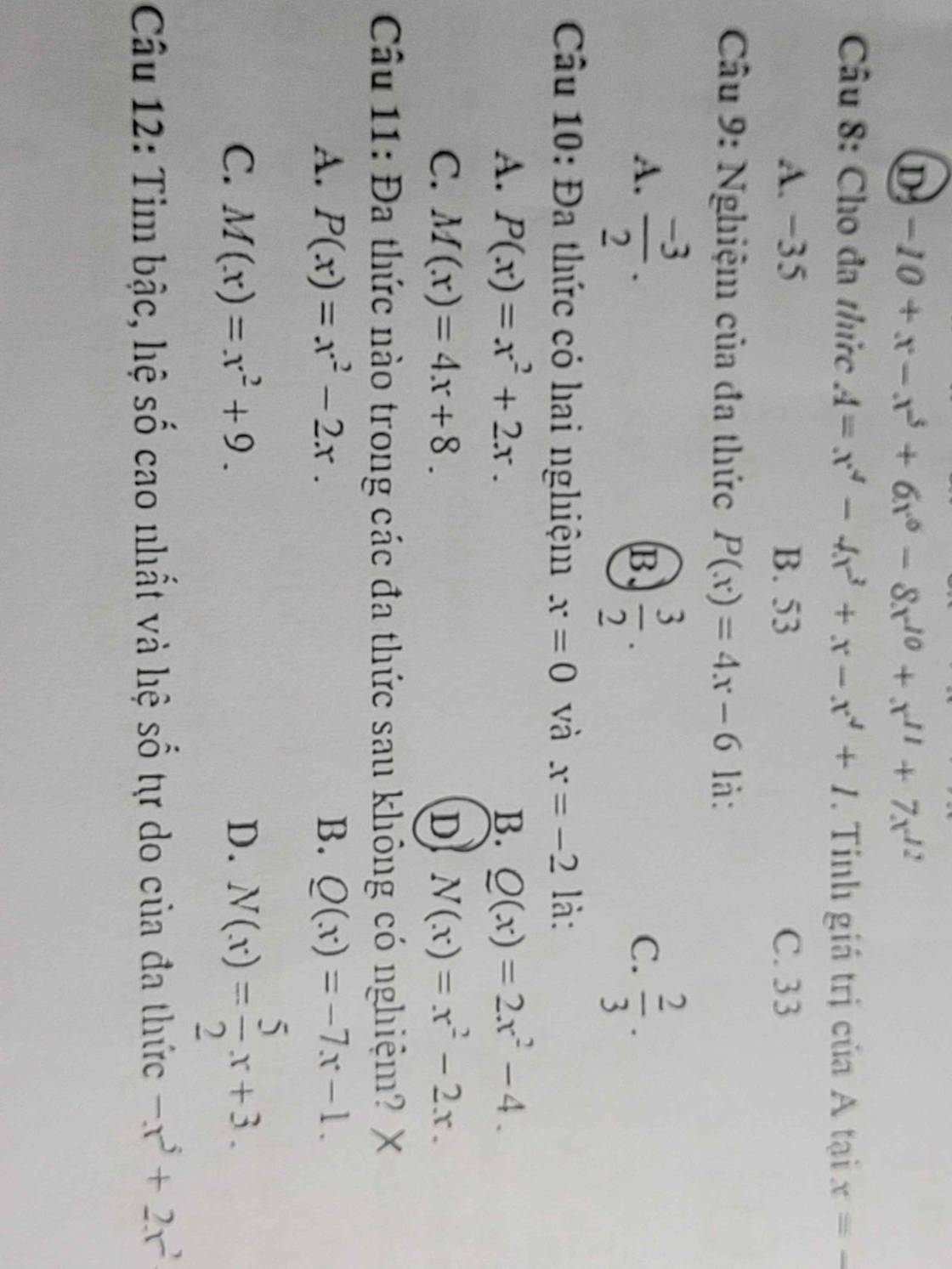
i: Đặt x2+2x+3=0
=>\(x^2+2x+1+2=0\)
=>\(\left(x+1\right)^2+2=0\)(vô lý)
=>\(x\in\varnothing\)
k: \(3x^2+8x-11=0\)
=>\(3x^2+11x-3x-11=0\)
=>(3x+11)(x-1)=0
=>\(\left[{}\begin{matrix}x=-\dfrac{11}{3}\\x=1\end{matrix}\right.\)
m: Đặt \(x^2+8x+20=0\)
=>\(x^2+8x+16+4=0\)
=>\(\left(x+4\right)^2+4=0\)(vô lý)
=>\(x\in\varnothing\)