1) \(\sqrt{2x-1}=\sqrt{x^2+4x-4}\left(Đk:x\ge\dfrac{1}{2}\right)\)

\(\Leftrightarrow2x-1=x^2+4x-4\)

\(\Leftrightarrow x^2+2x-3=0\)

\(\Leftrightarrow\left(x-1\right)\left(x+3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(TM\right)\\x=-3\left(L\right)\end{matrix}\right.\)

Vậy \(S=\left\{1\right\}\)

2) \(\sqrt{x^2-4x+3}=x-3\left(Đk:x\ge3\right)\)

\(\Leftrightarrow\left(x-3\right)^2=x^2-4x+3\)

\(\Leftrightarrow x^2-6x+9=x^2-4x+3\)

\(\Leftrightarrow2x=6\)

\(\Leftrightarrow x=3\)

Vậy \(S=\left\{3\right\}\)

Để phương trình: \(x^2-2\left(m-1\right)x+4m+8=0\) có nghiệm

\(\Rightarrow\Delta\ge0\)

\(\Leftrightarrow4\left(m-1\right)^2-4\left(4m+8\right)\ge0\)

\(\Leftrightarrow4m^2-8m+4-16m-32\ge0\)

\(\Leftrightarrow4m^2-24m-28\ge0\)

\(\Leftrightarrow m^2-6m-7\ge0\)

\(\Leftrightarrow\left(m+1\right)\left(m-7\right)\ge0\)

\(\Rightarrow m\in(-\infty;-1]\cup[7;+\infty)\)

Gọi F, S lần lượt là tập hợp các bạn thích chơi đá bóng, bơi lội.

Dùng công thức \(\left|F\cup S\right|+\left|F\cap S\right|=\left|F\right|+\left|S\right|\) 

\(\Rightarrow\left|F\cap S\right|=\left|F\right|+\left|S\right|-\left|F\cup S\right|\) \(=18+15-28=5\)

Vậy có 5 bạn thích cả đá bóng và bơi lội.

Bạn cần hỏi đáp điều gì không nhỉ?

Bạn cần làm gì?

chỉ nhờ vào tương lai

Tùy em nhá, có thể là em sẽ chỉ đc loại khá thôi em ạ, giỏi thì phải tất cả trên 9 cơ em ạ.

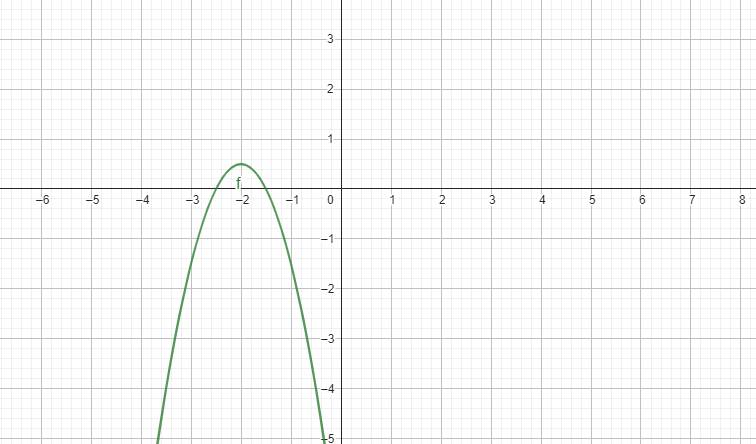
 Xét parabol \(\left(C_m\right):y=-2x^2-\left(2m-1\right)x+6-3m\), ta có \(\Delta=\left[-\left(2m-1\right)\right]^2-4\left(-2\right)\left(6+3m\right)=4m^2+20m+49\)

  Gọi \(I_m\) là đỉnh của \(\left(C_m\right)\) thì \(I_m\left(\dfrac{-2m+1}{4};\dfrac{4m^2+20m+49}{8}\right)\)

  Để hàm số đã cho nghịch biến trong khoảng \(\left(-2;+\infty\right)\) thì \(\dfrac{-2m+1}{4}=-2\Leftrightarrow m=\dfrac{9}{2}\)

Tao đéo biết thằng Nguyễn Huy Hung nha ☹

Cách 1: Dùng định lý Menelaus đảo:

Từ đề bài, ta có \(\dfrac{BD}{BC}=\dfrac{2}{3}\), \(\dfrac{MC}{MA}=\dfrac{3}{2}\), \(\dfrac{IA}{ID}=1\)

\(\Rightarrow\dfrac{BD}{BC}.\dfrac{MC}{MA}.\dfrac{IA}{ID}=1\)

Theo định lý Menelaus đảo, suy ra B, I, M thẳng hàng.

Cách 2: Dùng vector

 Ta có \(\overrightarrow{BI}=\dfrac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{BD}\right)\)

\(=\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{2}.\dfrac{2}{3}\overrightarrow{BC}\)

\(=\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{3}\overrightarrow{BC}\) 

\(=\dfrac{1}{6}\left(3\overrightarrow{BA}+2\overrightarrow{BC}\right)\)

Lại có \(\overrightarrow{BM}=\dfrac{MC}{AC}\overrightarrow{BA}+\dfrac{MA}{AC}\overrightarrow{BC}\)

\(=\dfrac{3}{5}\overrightarrow{BA}+\dfrac{2}{5}\overrightarrow{BC}\)

\(=\dfrac{1}{5}\left(3\overrightarrow{BA}+2\overrightarrow{BC}\right)\)

\(=\dfrac{6}{5}.\dfrac{1}{6}\left(3\overrightarrow{BA}+2\overrightarrow{BC}\right)\)

\(=\dfrac{6}{5}\overrightarrow{BI}\)

Vậy \(\overrightarrow{BM}=\dfrac{6}{5}\overrightarrow{BI}\), suy ra B, I, M thẳng hàng. 

Có \(\overrightarrow{MA}+k\overrightarrow{MB}+\left(1-k\right)\overrightarrow{MC}=\overrightarrow{0}\)

\(\Leftrightarrow\left(\overrightarrow{MA}+\overrightarrow{MC}\right)+k\left(\overrightarrow{MB}-\overrightarrow{MC}\right)=\overrightarrow{0}\)       (1)

Gọi N là trung điểm của AC thì 

(1) \(\Leftrightarrow2\overrightarrow{MN}+k\overrightarrow{CB}=\overrightarrow{0}\)

\(\Leftrightarrow\overrightarrow{NM}=\dfrac{k}{2}\overrightarrow{CB}\)      (2)

Vậy điểm M là điểm thỏa mãn \(\overrightarrow{NM}=\dfrac{k}{2}\overrightarrow{CB}\) với N là trung điểm AC.