Điều này tương đương ko có cạnh nào của lục giác được tạo ra từ 2 đỉnh liền nhau của đa giác

Chọn 1 đỉnh \(A_1\) có 108 cách

Chọn 5 đỉnh còn lại \(A_2A_3A_4A_5A_6\) sao cho giữa \(A_1A_2\) có \(x_1\) đỉnh, giữa \(A_2A_3\) có \(x_2\) đỉnh, ..., giữa \(A_6A_1\) có \(x_6\) đỉnh với \(x_1;x_2;...;x_6\) là các số nguyên dương

\(\Rightarrow x_1+x_2+x_3+x_4+x_5+x_6=108-6=102\)

Theo nguyên lý chia kẹo Euler, pt trên có \(C_{101}^5\) bộ nghiệm nguyên dương

\(\Rightarrow\dfrac{108.C_{101}^5}{6}\) lục giác thỏa mãn

 Cho phương trình bậc hai \(x^2\) + 2\(x\) - m² + 2m - 3 = 0

a; Chứng minh phương trình luôn có hai nghiệm phân biệt.

Ta có \(x^2\) + 2\(x\) - m² + 2m - 3 = 0

    ⇒ △^, = 1²  - ( - m² + 2m - 3) = 1 + m² - 2m + 3 = (m - 1)² + 3 

      (m - 1)² ≥ 0 ∀ m; ⇒ (m - 1)² + 3 ≥ 3 ∀ m

       ⇒△^, = (m -1)² + 3 ≥ 3 > 0 ∀ m

Vậy phương trình đã cho luôn có hai nghiệm phân biệt với mọi giá trị của m.

b; Theo chứng minh trên ta có phương trình đã cho luôn có hai nghiệm phân biệt với mọi giá trị của m, áp dụng hệ thức Vi-et ta có:

\(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1.x_2=-m^2+2m-3\end{matrix}\right.\) (1)

Mặt khác ta có: |\(x_1\) - \(x_2\)| = 4 ⇒ (|\(x_1\) - \(x_2\)|)² = 4² ⇒ (\(x_1\) - \(x_2\))²  = 16

                         (\(x_1\) + \(x_2\))² - 4\(x_2\)\(x_2\) = 16 (2)

Thay (1) vào (2) ta có: (-2)² - 4.(- m² + 2m - 3) = 16

                                       4 + 4m² - 8m + 12  = 16

                                             4m² - 8m = 16 - 12 - 4

                                             4m² - 8m = 0

                                              4m.(m - 2) = 0

                                                \(\left[{}\begin{matrix}m=0\\m-2=0\end{matrix}\right.\)

                                                \(\left[{}\begin{matrix}m=0\\m=2\end{matrix}\right.\)

Vậy để phương trình đã cho có hai nghiệm phân biệt thỏa mãn đề bài thì 

m \(\in\) {0; 2}

a.

\(\Delta'=1-\left(-m^2+2m-3\right)=m^2-2m+4=\left(m-1\right)^2+3>0;\forall m\)

\(\Rightarrow\) Phương trình luôn có 2 nghiệm pb với mọi m

b.

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1x_2=-m^2+2m-3\end{matrix}\right.\)

\(\left|x_1-x_2\right|=4\)

\(\Leftrightarrow\left(x_1-x_2\right)^2=16\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=16\)

\(\Leftrightarrow4-4\left(-m^2+2m-3\right)=16\)

\(\Leftrightarrow m^2-2m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=2\end{matrix}\right.\)

        Đây là toán nâng cao chuyên đề chuyển động, cấu trúc nâng cao thi chuyên, thi học sinh giỏi các cấp, thi violympic. Hôm nay Olm.vn sẽ hướng dẫn các em giải chi tiết dạng này bằng tỉ số vận tốc như sau:

                                Giải:

           Thời gian xe máy đi từ B về đến C là:

            9 giờ 36 phút - 7 giờ 30 phút  = \(\dfrac{21}{10}\) (giờ)

  Vì cùng một quãng đường thì thời gian tỉ lệ nghịch với vận tốc nên nếu đi bằng ô tô từ B đến C hết thời gian là:

                       \(\dfrac{21}{10}\) : \(\dfrac{5}{3}\) = \(\dfrac{63}{50}\) (giờ)

 Thời gian ô tô đi từ A đến C là:

             9 giờ 36 phút - 6 giờ 45 phút = 2 giờ 51 phút

                      2 giờ 51 phút = \(\dfrac{57}{20}\) giờ 

Nếu đi bằng xe ô tô trên cả quãng đường từ A đến B thì đi hết thời gian là:

                     \(\dfrac{57}{20}\) + \(\dfrac{63}{50}\) = \(\dfrac{411}{100}\) (giờ)

Vận tốc của ô tô là: 226,05 : \(\dfrac{411}{100}\) = 55 (km/h)

Vận tốc của xe máy là: 55 : \(\dfrac{5}{3}\) = 33 (km/h)

Đáp số: Vận tốc xe ô tô là: 55km/h

             Vận tốc xe máy là là: 33 km/h

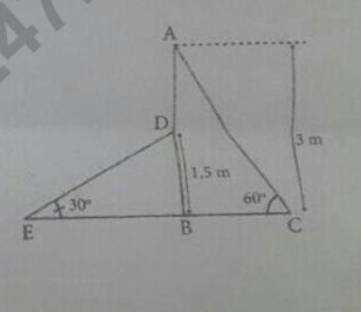
Trong tam giác vuông BDE:

\(DE=\dfrac{BD}{sinE}=\dfrac{1,5}{sin30^0}=3\left(m\right)\)

Trong tam giác vuông ABC:

\(AC=\dfrac{AB}{sinC}=\dfrac{3}{sin60^0}=2\sqrt{3}\left(m\right)\)

Ta có:

\(CE=BE+BC=\dfrac{BD}{tanE}+\dfrac{AB}{tanC}=\dfrac{1,5}{tan30^0}+\dfrac{3}{tan60^0}=\dfrac{5\sqrt{3}}{2}\left(m\right)\)

a: Sửa đề; MF vuông góc với AC tại F

Xét ΔBEM vuông tại E và ΔCFM vuông tại F có

BM=CM

\(\widehat{MBE}=\widehat{MCF}\)

Do đó: ΔBEM=ΔCFM

b: Ta có: ΔBEM=ΔCFM

=>ME=MF

=>M nằm trên đường trung trực của EF(1)

ta có: ΔBEM=ΔCFM

=>BE=CF

Ta có: AE+EB=AB

AF+FC=AC

mà BE=FC và AB=AC

nên AE=AF

=>A nằm trên đường trung trực của EF(2)

Từ (1),(2) suy ra AM là đường trung trực của EF

c: Xét ΔABC có \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)

nên EF//BC

d: Xét ΔABD vuông tại B và ΔACD vuông tại C có

AD chung

AB=AC

Do đó: ΔABD=ΔACD

=>DB=DC

=>D nằm trên đường trung trực của BC(3)

ta có: AB=AC

=>A nằm trên đường trung trực của BC(4)

ta có: MB=MC

=>M nằm trên đường trung trực của BC(5)

Từ (3),(4),(5) suy ra A,M,D thẳng hàng

Không gian mẫu: \(C_{2n}^3\)

Đa giác đều 2n đỉnh có n đường chéo đi qua tâm O

Chọn 1 đường chéo có n cách

Chọn 1 điểm kết hợp với đường chéo tạo thành tam giác vuông (nội tiếp chắn nửa đường tròn): có \(2n-2\) cách

\(\Rightarrow n\left(2n-2\right)\) tam giác vuông

Xác suất: \(P=\dfrac{n\left(2n-2\right)}{C_{2n}^3}=\dfrac{1}{13}\Rightarrow26n\left(n-1\right)=C_{2n}^3\)

\(\Rightarrow26n\left(n-1\right)=\dfrac{n.\left(2n-1\right)\left(2n-2\right)}{3}\)

\(\Rightarrow n^2-21n+20=0\Rightarrow\left[{}\begin{matrix}n=1\left(loại\right)\\n=20\end{matrix}\right.\)

Trên \(\left[0;3\right]\) hàm \(y=x^2-3x\) âm nên ta cần "xoay" nó lên thành \(y=3x-x^2\)

Khi đó:

Pt hoành độ giao điểm trên \(\left[0;3\right]\): \(3x-x^2=x\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)

Pt hoành độ giao điểm với \(x>3\): \(x^2-3x=x\Rightarrow x=4\)

Do đó:

\(V=\pi\int\limits^2_0\left(3x-x^2\right)^2dx+\pi\int\limits^4_2x^2dx-\pi\int\limits^4_3\left(x^2-3x\right)^2dx=\dfrac{611\pi}{30}\)

\(\Rightarrow18a-300b=1998\)

Gọi số có dạng \(\overline{a_1a_2a_3a_4a_6a_6}\)

Do số chẵn nên \(a_6\) có 5 cách chọn

\(a_5\) có 9 cách chọn (khác \(a_6\))

\(a_4\) có 9 cách chọn (khác \(a_5\))

....

\(a_2\) có 9 cách chọn (khác \(a_3\))

\(a_1\) có 8 cách chọn (khác 0 và \(a_2\))

\(\Rightarrow5.9.9.9.9.8\) số thỏa mãn

Chia các số từ 1 đến 100 thành 3 nhóm: 

\(A=\left\{3;6;9;...;99\right\}\) gồm 33 số chia hết cho 3

\(B=\left\{1;4;7;...;100\right\}\) gồm 34 số chia 3 dư 1

\(C=\left\{2;5;8;...;98\right\}\) gồm 33 số chia 3 dư 2

Tổng 3 số chia hết cho 3 khi: cả 3 số cùng số dư khi chia 3 - hay cùng thuộc 1 tập, 3 số thuộc 3 tập khác nhau

\(\Rightarrow C_{33}^3+C_{34}^3+C_{33}^3+C_{33}^1.C_{34}^1.C_{33}^1\) trường hợp thỏa mãn

Xác suất: \(P=\dfrac{C_{33}^3+C_{34}^3+C_{33}^3+C_{33}^1.C_{34}^1.C_{33}^1}{C_{100}^3}=\dfrac{817}{2450}\)

Từ đề bài ta suy ra trong 7 chữ số có đúng 1 chữ số có mặt 2 lần, 6 chữ số còn lại có mặt đúng 1 lần

Không gian mẫu: \(7.C_8^2.6!=141120\) số

TH1: chữ số có mặt 2 lần là chữ số lẻ.

Chọn chữ số lẻ lặp 2 lần có: 4 cách

Xếp vị trí cho 4 chữ số lẻ (có 1 số lặp 2 lần): \(C_5^2.3!=60\) cách

5 chữ số lẻ tạo thành 6 khe trống, xếp 3 chữ số chẵn vào 6 khe trống: \(A_6^3\) cách

TH2: chữ số có mặt 2 lần là chữ số chẵn.

Chọn chữ số chẵn có mặt 2 lần: 3 cách

Xếp vị trí cho 4 chữ số lẻ: \(4!\) cách

4 chữ số lẻ tạo thành 5 khe trống, chọn 2 vị trí cho chữ số chẵn lặp 2 lần: \(C_5^2\) cách

Xếp 3 chữ số chẵn còn lại: \(3!\) cách

\(\Rightarrow4.60.A_6^3+3.4!.C_5^2.3!=33120\) số

Xác suất: \(\dfrac{33120}{141120}=\dfrac{23}{98}\)