hòa tan 50 g muối vào trong 150 gam nước Tính tỉ số phần trăm muối trong dung dịch nước muối
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ: x<>0
\(\dfrac{2}{5}\left(\dfrac{1}{2}-\dfrac{2}{2x}\right)-\dfrac{3}{5}\left(\dfrac{1}{3x}-\dfrac{10}{3}\right)=-\dfrac{1}{4}\)
=>\(\dfrac{1}{5}-\dfrac{2}{5x}-\dfrac{1}{5x}+2=-\dfrac{1}{4}\)
=>\(-\dfrac{3}{5x}+\dfrac{11}{5}=-\dfrac{1}{4}\)
=>\(-\dfrac{3}{5x}=-\dfrac{1}{4}-\dfrac{11}{5}=\dfrac{-49}{20}\)
=>\(\dfrac{3}{5x}=\dfrac{49}{20}\)
=>\(5x=20\cdot\dfrac{3}{49}=\dfrac{60}{49}\)
=>\(x=\dfrac{12}{49}\left(nhận\right)\)

\(A=\dfrac{1.2+2.1.2.2+3.1.3.2+4.1.4.2+5.1.5.2}{3.4+2.3.2.4+3.3.3.4+4.3.4.4+5.3.5.4}\)
\(=\dfrac{1.2+1.2.2^2+1.2.3^2+1.2.4^2+1.2.5^2}{3.4+3.4.2^2+3.4.3^2+3.4.4^2+3.4.5^2}\)
\(=\dfrac{1.2.\left(1+2^2+3^2+4^2+5^2\right)}{3.4.\left(1+2^2+3^2+4^2+5^2\right)}\)
\(=\dfrac{1.2}{3.4}=\dfrac{1}{6}\)

12:
\(S=\dfrac{1}{2}+\dfrac{2}{4}+...+\dfrac{10}{2^{10}}\)
\(=\dfrac{1}{2^1}+\dfrac{2}{2^2}+...+\dfrac{10}{2^{10}}\)
\(=\dfrac{1+1}{2^{1-1}}-\dfrac{1+2}{2^1}+\dfrac{2+1}{2^{2-1}}-\dfrac{2+2}{2^2}+...+\dfrac{10+1}{2^{10-1}}-\dfrac{10+2}{2^{10}}\)
\(=2-\dfrac{12}{2^{10}}=\dfrac{2^{11}-12}{2^{10}}\)

\(\dfrac{x-1}{2}=\dfrac{2-x}{3}\)
\(\Rightarrow3\cdot\left(x-1\right)=2\cdot\left(2-x\right)\)
\(\Rightarrow3x-3=4-2x\)
\(\Rightarrow3x+2x=4+3\)
\(\Rightarrow5x=7\)
\(\Rightarrow x=\dfrac{7}{5}\)
\(x-\dfrac{1}{2}=2-\dfrac{x}{3}\)
\(x+\dfrac{x}{3}=2+\dfrac{1}{2}\)
\(x\left(1+\dfrac{1}{3}\right)=\dfrac{5}{2}\)
\(x\times\dfrac{4}{3}=\dfrac{5}{2}\)
\(x=\dfrac{5}{2}:\dfrac{4}{3}\)
\(x=\dfrac{15}{8}\)

Câu 6:
a: MB=2MC
=>\(\dfrac{CM}{CB}=\dfrac{1}{3};\dfrac{BM}{BC}=\dfrac{2}{3}\)
Ta có: BM=2/3BC
=>\(S_{MBE}=\dfrac{2}{3}\cdot S_{BEC}\)
Vì CM=1/3CB
nên \(S_{MCD}=\dfrac{1}{3}\cdot S_{BCD}\)
Xét ΔMAB và ΔMEC có
\(\widehat{MAB}=\widehat{MEC}\)(hai góc so le trong, AB//EC)
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
Do đó: ΔMAB~ΔMEC
=>\(\dfrac{AB}{EC}=\dfrac{BM}{CM}=2\)
=>\(\dfrac{CD}{CE}=2\)
=>\(S_{BCD}=2\cdot S_{BCE}\)
=>\(\dfrac{1}{3}\cdot S_{BCD}=\dfrac{2}{3}\cdot S_{BCE}\)
=>\(S_{MBE}=S_{MCD}\)
b: \(MB=\dfrac{2}{3}BC\)
mà BC=AD
nên \(\dfrac{MB}{AD}=\dfrac{2}{3}\)
Xét ΔOBM và ΔODA có
\(\widehat{OBM}=\widehat{ODA}\)(BM//DA)
\(\widehat{BOM}=\widehat{DOA}\)(hai góc đối đỉnh)
Do đó: ΔOBM~ΔODA
=>\(\dfrac{OB}{OD}=\dfrac{MB}{DA}=\dfrac{2}{3}\)

Bài 43: Sửa đề: Trên tia Ox
a: Trên tia Ox, ta có: OA<OB
nên A nằm giữa O và B
=>OA+AB=OB
=>AB+4=7
=>AB=3(cm)
b: Vì BA và BD là hai tia đối nhau
nên B nằm giữa A và D
=>AD=AB+BD=3+1=4(cm)
c: Vì OA=AD(=4cm)
nên A là trung điểm của OD
Bài 44:
\(S=\dfrac{3^2}{1\cdot3}+\dfrac{3^2}{3\cdot5}+...+\dfrac{3^2}{2021\cdot2023}\)
\(=\dfrac{9}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{2021\cdot2023}\right)\)
\(=\dfrac{9}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2021}-\dfrac{1}{2023}\right)\)
\(=\dfrac{9}{2}\left(1-\dfrac{1}{2023}\right)=\dfrac{9}{2}\cdot\dfrac{2022}{2023}=\dfrac{9099}{2023}\)

\(\dfrac{11}{19}.\dfrac{12}{29}-\dfrac{11}{19}.\dfrac{2}{29}+\dfrac{11}{19}.\dfrac{19}{29}\)
\(=\dfrac{11}{19}.\left(\dfrac{12}{29}-\dfrac{2}{29}+\dfrac{19}{29}\right)\)
\(=\dfrac{11}{19}.1\)
\(=\dfrac{11}{19}\)

3/4 giá niêm yết là:
\(\dfrac{3}{4}\cdot300000=225000\left(đồng\right)\)
Giá vốn là \(225000\cdot\dfrac{100}{125}=180000\left(đồng\right)\)
Để lãi 40% so với giá vốn thì giá tiền cửa hàng cần bán là:
\(180000\left(1+40\%\right)=180000\cdot1,4=252000\left(đồng\right)\)
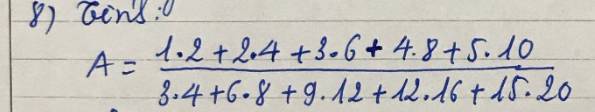
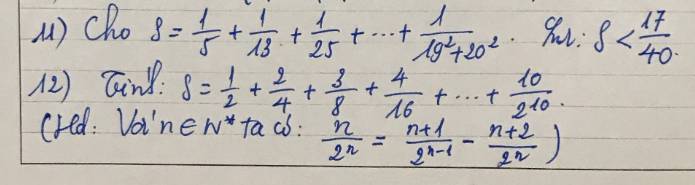


Giải:
Khối lượng dung dịch nước muối là:
50 + 150 = 200 (gam)
Tỉ số phần trăm muối có trong dung dịch nước muối là:
50 : 200 x 100% = 25%
Kết luận: tỉ số phần trăm muối trong dung dịch nước muối là 25%