Đánh sai đề kìa :v \(\frac{1}{\sqrt{b^2-ab+2a^2}}\) mới đúng. 

Cho \(a=b\rightarrow S=2\sqrt{2}\). Ta cm đây là gtln của S.

\(S\le\left(a+b\right)\sqrt{2\left(\frac{1}{a^2-ab+2b^2}+\frac{1}{b^2-ab+2a^2}\right)}\le2\sqrt{2}\)

\(\Leftrightarrow\left(5a^2-6ab+5b^2\right)\left(a-b\right)^2\ge0\)(bình phương lên quy đồng là xong)

Đẳng thức xảy ra khi a  = b.

Đúng ko đấy ạ, sao em quy đồng lên ra \(20a^2b^2-16\left(a^3b+ab^3\right)+5\left(a^4+b^4\right)\)

Nhưng \(\left(a-b\right)^2\left(5a^2-6ab+5b^2\right)=5\left(a^4+b^4\right)+22a^2b^2-16\left(a^3b+ab^3\right)\)

Ta có:

(sin α+cos α)^2

=sin^2α + 2sin α cos α + cos^2 α

=1+2sin α cos α

Nên A đúng

(sin α−cos α)^2

=sin^2 α−2sin α cos α+cos^2α

=(sin^2α+cos^2α)−2sin α cos α

=1−2sin α cos α

Nên B đúng

cos^4 α−sin^4 α

=(cos^2 α−sin^2 α)(cos^2 α+sin^2 α)

=(cos^2 α−sin^2 α).1

=cos^2 α−sin^2 α

Nên C đúng

cos^4 α+sin^4 α

=(sin^2 α+cos^2 α )^2−2sin^2 α cos^2 α

=1−2 sin^2 α cos^2 α.

Nên D sai chọn D

ko bít có đúng ko nx

Bạn ơi! Toán từ lớp 10 trở lên bạn vào hoc 24 để gửi câu hỏi nhé!

Bài này câu D sai. 

Bạn thay \(\alpha=\frac{\pi}{2}\) vào thử nhé!

Ta có cos45 độ + sin45 độ=√2/2+√2/2=√2

Chọn (B).

Ta có sin0 độ + cos0 độ =0+1=1 nên A sai.

sin90 độ + cos90 độ =1+0=1 nên B đúng.

sin180 độ + cos180 độ=0+(−1)=−1 nên C đúng.

sin60 độ + cos60 độ =√3/2+1/2=√3+1/2 nên D đúng.

Chọn (A).

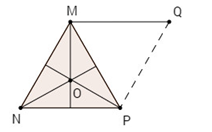
Vẽ −−→MQ=−−→NPMQ→=NP→

(MN→,NP→)=(MN→,MQ→)=120 độ.

Chọn (A).

Ngoài ra, có thể tính được:

(−−→MO,−−→ON)=60 độ \

(−−−→MN,−−→OP)=90 độ

(−−−→MN,−−→MP)=60 độ

ho O là tâm đường tròn ngoại tiếp tam giác đều MNP. Góc nào sau đây bằng 12001200 ? (

A) (−−−→MN,−−→NP)(MN→,NP→);

(B) (−−→MO,−−→ON)(MO→,ON→);

(C) (−−−→MN,−−→OP)(MN→,OP→);

(D) (−−−→MN,−−→MP)(MN→,MP→).

#Tiểu Cừu

+) \(P=\frac{\sqrt{x}+\sqrt{x^2-2x+1}+1}{\sqrt{x^2-2x+1}}=\frac{\sqrt{x}+\left|x-1\right|+1}{\left|x-1\right|}\)

+) \(x=a+1-\sqrt{1+a^2+\frac{a^2}{\left(a+1\right)^2}}\)

\(=a+1-\sqrt{\left(a+1\right)^2-2a+\frac{a^2}{\left(a+1\right)^2}}\)

\(=a+1-\sqrt{\left(a+1-\frac{a}{a+1}\right)^2}\) vì a > 0 => \(a+1-\frac{a}{a+1}=\frac{a^2+a+1}{a+1}>0\)

\(=a+1-\left(a+1-\frac{a}{a+1}\right)=\frac{a}{a+1}\)

=> \(\left|x-1\right|=\left|\frac{a}{a+1}-1\right|=\left|-\frac{1}{a+1}\right|=\frac{1}{a+1}\)

=> \(P=\frac{\sqrt{\frac{a}{a+1}}+\frac{1}{a+1}+1}{\frac{1}{a+1}}=\sqrt{a\left(a+1\right)}+a+2\)

99999999 ok

Bạn xem lại đề, tổng của các chữ số hay tích của các chữ số hay hiệu hay gì đó? 

Tham khảo câu trả lời tại đây bạn nhé !

https://olm.vn/hoi-dap/detail/224113518607.html

Câu hỏi của An Van - Toán lớp 10 - Học toán với OnlineMath

Chúc bạn học tốt ^_^

Bài làm:

Ta có: \(n^3+3n^2+5n=\left(n^3+3n^2+2n\right)+3n\)

\(=n\left(n+1\right)\left(n+2\right)+3n\)

Vì n(n+1)(n+2) là tích 3 STN liên tiếp 

=> n(n+1)(n+2) chia hết cho 3, mà 3n chia hết cho 3

=> đpcm

Cho: \(x\ne-1\)và \(y\ne-1\)

g/s: \(x+y+xy=-1\)

<=> \(\left(x+xy\right)+\left(y+1\right)=0\)

<=> \(\left(x+1\right)\left(y+1\right)=0\)

<=> \(\orbr{\begin{cases}x=-1\\y=-1\end{cases}}\) vô lí vì trái với gỉa thiết 

Vậy  \(x\ne-1\)và \(y\ne-1\) thì \(x+y+xy\ne-1\)