
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ: x<>-2y
\(\left\{{}\begin{matrix}\dfrac{1}{x+2y}+y=-2\\\dfrac{2}{x+2y}-3y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{3}{x+2y}+3y=-6\\\dfrac{2}{x+2y}-3y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{5}{x+2y}=5\\\dfrac{2}{x+2y}-3y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+2y=1\\3y=\dfrac{2}{x+2y}-1=2-1=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{1}{3}\\x=1-2y=1-2\cdot\dfrac{1}{3}=1-\dfrac{2}{3}=\dfrac{1}{3}\end{matrix}\right.\left(nhận\right)\)

Ta có:
\(a^4+\dfrac{1}{4}=\left(a^2+\dfrac{1}{2}\right)^2-a^2=\left(a^2+a+\dfrac{1}{2}\right)\left(a^2-a+\dfrac{1}{2}\right)\)
\(=\left(a^2+a+\dfrac{1}{2}\right)\left(a^2-2a+1+a-1+\dfrac{1}{2}\right)\)
\(=\left(a^2+a+\dfrac{1}{2}\right)\left[\left(a-1\right)^2+\left(a-1\right)+\dfrac{1}{2}\right]\)
Do đó:
\(K=\dfrac{\left(2^2+2+\dfrac{1}{2}\right)\left(1^2+1+\dfrac{1}{2}\right)...\left(\left(2n\right)^2+2n+\dfrac{1}{2}\right)\left(\left(2n-1\right)^2+\left(2n-1\right)+\dfrac{1}{2}\right)}{\left(1^2+1+\dfrac{1}{2}\right)\left(0^2+0+\dfrac{1}{2}\right)...\left(\left(2n-1\right)^2+\left(2n-1\right)+\dfrac{1}{2}\right)\left(\left(2n-2\right)^2+\left(2n-2\right)+\dfrac{1}{2}\right)}\)
\(=\dfrac{\left(2n\right)^2+2n+\dfrac{1}{2}}{0^2+0+\dfrac{1}{2}}=8n^2+4n+1\)
\(=\left(2n\right)^2+\left(2n+1\right)^2\) là tổng của 2 SCP
ai giải hộ em câu này với
cho 30g hôn hợp c2h5oh với ch3cooh phản ứng hết với 100ml NaOH 1M
a) tính phần trăm kl các chất ban đầu
b)tính kl Na cần để phản ứng với lượng c2h5oh

Ta có: \(\left(x+y+z\right)^2=x^2+y^2+z^2\)
\(\Leftrightarrow x^2+y^2+z^2+2xy+2yz+2zx-x^2-y^2-z^2=0\)
\(\Leftrightarrow2\left(xy+yz+zx\right)=0\)
\(\Leftrightarrow xy+yz+zx=0\)
Đặt \(\dfrac{1}{x}=a;\dfrac{1}{y}=b;\dfrac{1}{z}=c\Rightarrow\dfrac{3}{xyz}=3abc\)
Lại có: \(xy+yz+zx=0\Rightarrow\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ca}=0\)
\(\Leftrightarrow\dfrac{a+b+c}{abc}=0\Leftrightarrow a+b+c=0\)
Khi đó, xét hiệu: \(\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}-\dfrac{3}{xyz}\)
\(=a^3+b^3+c^3-3abc\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)^3-3\left(a+b\right)c\left(a+b+c\right)-3ab\left(a+b+c\right)\)
\(=0\) (do \(a+b+c=0\))
\(\Rightarrow\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}=\dfrac{3}{xyz}\) (đpcm)
\(Toru\)



a: \(\text{Δ}=\left(2m+1\right)^2-4\cdot\left(m^2+\dfrac{1}{2}\right)\)
\(=4m^2+4m+1-4m^2-2=4m-1\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
=>4m-1>0
=>m>1/4
b: Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m+1\\x_1x_2=\dfrac{c}{a}=m^2+\dfrac{1}{2}\end{matrix}\right.\)
\(M=\left(x_1-1\right)\left(x_2-1\right)\)
\(=x_1x_2-\left(x_1+x_2\right)+1\)
\(=m^2+\dfrac{1}{2}-2m-1+1\)
\(=m^2-2m+\dfrac{1}{2}\)
\(=m^2-2m+1-\dfrac{1}{2}=\left(m-1\right)^2-\dfrac{1}{2}>=-\dfrac{1}{2}\forall m\)
Dấu '=' xảy ra khi m-1=0
=>m=1(nhận



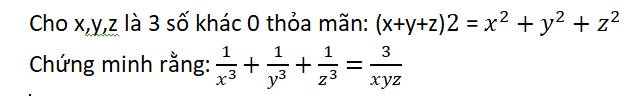

1: Thay x=9 vào B, ta được:
\(B=\dfrac{1}{3-1}=\dfrac{1}{2}\)
2: P=A-B
\(=\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\)
\(=\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\)
\(=\dfrac{x+2+\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{-\sqrt{x}+1+x-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}=\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)