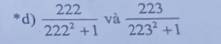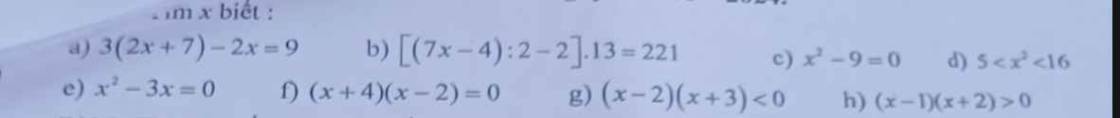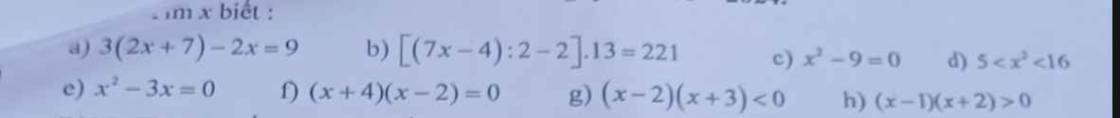Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`#3107.101107`
`a)`
- Tổng của 2 số hữu tỉ khác dấu: \(-\dfrac{4}{15}=-\dfrac{13}{15}+\dfrac{9}{15}\)
`b)`
- Tích cảu 2 số hữu tỉ: \(-\dfrac{4}{15}=-\dfrac{8}{15}\cdot\dfrac{1}{2}\)
`c)`
Thương của 2 số hữu tỉ: \(-\dfrac{4}{15}=-\dfrac{16}{15}\div2\)

a) \(\dfrac{2x+1}{9}=\dfrac{5}{x+1}\left(x\ne-1\right)\)
\(\Rightarrow\left(2x+1\right)\left(x+1\right)=9\cdot5=45\)
\(\Rightarrow2x^2+2x+x+1=45\)
\(\Rightarrow2x^2+3x-44=0\)
\(\Rightarrow2x^2+11x-8x-44=0\)
\(\Rightarrow x\left(2x+11\right)-4\left(2x+11\right)=0\)
\(\Rightarrow\left(x-4\right)\left(2x+11\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\2x=-11\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-\dfrac{11}{2}\end{matrix}\right.\)
b) \(\dfrac{2x-1}{21}=\dfrac{3}{2x+1}\left(x\ne-\dfrac{1}{2}\right)\)
\(\Rightarrow\left(2x-1\right)\left(2x+1\right)=21\cdot3=63\)
\(\Rightarrow4x^2-1=63\)
\(\Rightarrow4x^2=64\)
\(\Rightarrow\left(2x\right)^2=8^2\)
\(\Rightarrow\left[{}\begin{matrix}2x=8\\2x=-8\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)
c) \(\dfrac{2x-1}{2}=\dfrac{5}{x}\left(x\ne0\right)\)
\(\Rightarrow x\left(2x-1\right)=5\cdot2=10\)
\(\Rightarrow2x^2-x=10\)
\(\Rightarrow2x^2-x-10=0\)
\(\Rightarrow2x^2+4x-5x-10=0\)
\(\Rightarrow2x\left(x+2\right)-5\left(x+2\right)=0\)
\(\Rightarrow\left(2x-5\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}2x=5\\x=-2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-2\end{matrix}\right.\)
d) \(\dfrac{x-3}{3}=\dfrac{2x+1}{5}\)
\(\Rightarrow15\cdot\dfrac{x-3}{3}=15\cdot\dfrac{2x+1}{5}\)
\(\Rightarrow5\left(x-3\right)=3\left(2x+1\right)\)
\(\Rightarrow5x-15=6x+3\)
\(\Rightarrow6x-5x=-18\)
\(\Rightarrow x=-18\)

Bài 1:
\(\dfrac{a}{b}-\dfrac{a+2009}{b+2009}=\dfrac{a\left(b+2009\right)-b\left(a+2009\right)}{b\left(b+2009\right)}\)
\(=\dfrac{2009a-2009b}{b\left(b+2009\right)}=\dfrac{2009\left(a-b\right)}{b\left(b+2009\right)}\)
Vì a>b>0 nên a-b>0; b>0; b+2009>0
=>\(\dfrac{2009\left(a-b\right)}{b\left(b+2009\right)}>0\)
=>\(\dfrac{a}{b}>\dfrac{a+2009}{b+2009}\)

Đặt 222=a
=>\(\dfrac{222}{222^2+1}=\dfrac{a}{a^2+1};\dfrac{223}{223^2+1}=\dfrac{\left(a+1\right)^2}{\left(a+1\right)^2+1}\)
\(\dfrac{a^2}{a^2+1}-\dfrac{\left(a+1\right)^2}{\left(a+1\right)^2+1}\)
\(=\dfrac{a^2\left[\left(a+1\right)^2+1\right]-\left(a+1\right)^2\left(a^2+1\right)}{\left(a^2+1\right)\left[\left(a+1\right)^2+1\right]}\)
\(=\dfrac{a^2\left(a^2+2a+2\right)-\left(a^2+2a+1\right)\left(a^2+1\right)}{\left(a^2+1\right)\left[\left(a+1\right)^2+1\right]}\)
\(=\dfrac{a^4+2a^3+2a^2-a^4-a^2-2a^3-2a-a^2-1}{\left(a^2+1\right)\left[\left(a+1\right)^2+1\right]}\)
\(=\dfrac{-2a-1}{\left(a^2+1\right)\left[\left(a+1\right)^2+1\right]}< 0\)
=>\(\dfrac{222}{222^2+1}< \dfrac{223}{223^2+1}\)

Bài 3
a; m - 2021 = 0 ⇒ m = 2021
Lập bảng ta có:
| m | 2021 |
| m - 2021 | - 0 + |
| 2024 | + + |
| \(x=\dfrac{m-2021}{2024}\) | - 0 + |
Theo bảng trên ta có \(x\) là số hữu tỉ dương khi và chỉ khi m > 2021
Vậy m > 2021
Bài 3b;
Bài 3
a; m - 2021 = 0 ⇒ m = 2021
Lập bảng ta có:
| m | 2021 |
| m - 2021 | - 0 + |
| 2024 | + + |
| \(x=\dfrac{m-2021}{2024}\) | - 0 + |
Theo bảng trên ta có \(x\) là số hữu tỉ âm khi và chỉ khi m < 2021
Vậy m < 2021

Bài 2a:
(2\(x\) + 5).35 = 38
2\(x\) + 5 = 38 : 35
2\(x\) + 5 = 33
2\(x\) + 5 = 27
2\(x\) = 27 - 5
2\(x\) = 22
\(x\) = 22: 2
\(x\) = 11
Vậy \(x\) = 11
b; 5\(x+2\) - 5\(x+1\) = 2500
5\(x+1\).(5 - 1) = 2500
5\(x+1\). 4 = 2500
5\(x+1\) = 2500 : 4
5\(x+1\) = 625
5\(x+1\) = 54
\(x+1\) = 4
\(x\) = 4 - 1
\(x\) = 3
Vậy \(x=3\)

f; (\(x\) + 4).(\(x-2\)) = 0
\(\left[{}\begin{matrix}x+4=0\\x-2=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-4\\x=2\end{matrix}\right.\)
Vậy \(x\) \(\in\) {-4; 2}
g; (\(x\) - 2).(\(x\) + 3) < 0
\(x\) - 2 = 0 ⇒ \(x\) = 2; \(x\) + 3 = 0 ⇒ \(x\) = -3
Lập bảng ta có:
| \(x\) | - 3 2 |
| \(x-2\) | - - 0 + |
| \(x\) + 3 | - 0 + + |
| (\(x-2\)).(\(x+3\)) | + 0 - 0 + |
Theo bảng trên ta có -3 < \(x\) < 2
Vậy -3 < \(x\) < 2

e) \(x^2-3x=0\)
\(\Leftrightarrow x\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
Vậy: ...
f) \(\left(x+4\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=2\end{matrix}\right.\)
Vậy: ...
g) \(\left(x-2\right)\left(x+3\right)< 0\)
TH1: \(\left\{{}\begin{matrix}x-2>0\\x+3< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>2\\x< -3\end{matrix}\right.\)
\(\Rightarrow x\in\varnothing\)
TH2: \(\left\{{}\begin{matrix}x-2< 0\\x+3>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< 2\\x>-3\end{matrix}\right.\)
\(\Rightarrow-3< x< 2\)
Vậy: ...
h) \(\left(x-1\right)\left(x+2\right)>0\)
TH1: \(\left\{{}\begin{matrix}x-1>0\\x+2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>1\\x>-2\end{matrix}\right.\)
\(\Rightarrow x>1\)
TH2: \(\left\{{}\begin{matrix}x-1< 0\\x+2< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< 1\\x< -2\end{matrix}\right.\)
\(\Rightarrow x< -2\)
Vậy: ...
a) \(3\left(2x+7\right)-2x=9\Leftrightarrow6x+21-2x=9\)
\(\Leftrightarrow4x+21=9\)
\(\Leftrightarrow4x=9-21=-12\)
\(\Leftrightarrow x=\dfrac{-12}{4}=-3\)
Vậy: ...
b) \(\left[\left(7x-4\right):2-2\right]\cdot13=221\)
\(\Leftrightarrow\left(7x-4\right):2-2=\dfrac{221}{13}=17\)
\(\Leftrightarrow\left(7x-4\right):2=17+2\)
\(\Leftrightarrow\left(7x-4\right):2=19\)
\(\Leftrightarrow7x-4=19\cdot2=38\)
\(\Leftrightarrow7x=42\)
\(\Leftrightarrow x=\dfrac{42}{7}=6\)
Vậy: ...
c) \(x^2-9=0\)
\(\Leftrightarrow x^2=9\)
\(\Leftrightarrow x=\pm\sqrt{9}\)
\(\Leftrightarrow x=\pm3\)
Vậy: ....
d) \(5< x^2< 16\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2>5\\x^2< 16\end{matrix}\right.\)
Với \(x^2>5\Rightarrow\left[{}\begin{matrix}x< -\sqrt{5}\\x>\sqrt{5}\end{matrix}\right.\) (1)
Với \(x^2< 16\Rightarrow-4< x< 4\) (2)
Từ (1) và (2) \(\left[{}\begin{matrix}-4< x< -\sqrt{5}\\\sqrt{5}< x< 4\end{matrix}\right.\)