Một vùng nọ có 88 thành phố và giữa hai thành phố bất kì được kết nối bởi một tuyến bay trực tiếp (hai chiều). Ủy ban Hàng không dự kiến cấp phép cho 88 hãng hàng không khai thác các tuyến bay đó, một tuyến bay bất kì sẽ được cấp phép cho đúng một trong các hãng đó và mỗi hãng khai thác ít nhất một tuyến bay. Hơn nữa, người ta muốn rằng với 3 hãng hàng không bất kì, luôn tìm được 3 thành phố sao cho 3 tuyến bay trực tiếp kết nối chúng được khai thác bởi 3 hãng đó. Hỏi Ủ ban Hàng không có thể thực hiện điều đó hay không?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

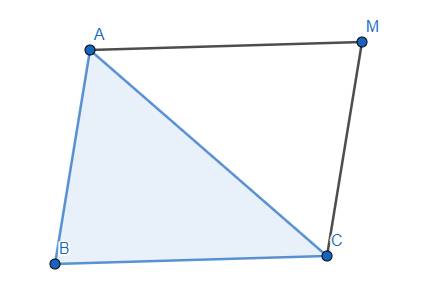
Ta thấy \(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MA}+\overrightarrow{BM}+\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{BA}=\overrightarrow{CM}\)
Như vậy, điểm M chính là đỉnh thứ tư của hình bình hành ABCM.

\(A\cap B=\left[-1;3\right]\\ A\cup B=\left(-\infty;5\right)\)

E = {\(x\)| \(x\) = 2k; k \(\in\)Z; - 25 ≤ k ≤ 20}

Lời giải:
Vì $\frac{AB}{AC}=\frac{3}{4}$ nên đặt $AB=3a; AC=4a$ $(a>0$)
Áp dụng hệ thức lượng trong tam giác vuông ta có:
$\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{AH^2}$
$\Rightarrow \frac{1}{(3a)^2}+\frac{1}{(4a)^2}=\frac{1}{16^2}$
$\Rightarrow \frac{25}{144a^2}=\frac{1}{16^2}$
$\Rightarrow a=\frac{20}{3}$
Áp dụng định lý pitago:
$HC=\sqrt{AC^2-AH^2}=\sqrt{(4a)^2-16^2}=\sqrt{(\frac{80}{3})^2-16^2}=\frac{64}{3}$ (cm)

\(36^{35}.12.234=\left(6^2\right)^{35}.2^2.3.18.13=6^{70}.2^2.3.3^2.2.13=2^{70}.3^{70}.2^3.3^3.13=2^{73}.3^{73}.13\)




 ...
... ...
...