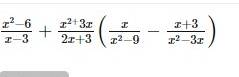ĐKXĐ: \(x\notin\left\{0;3;-3;-\dfrac{3}{2}\right\}\)

\(\dfrac{x^2-6}{x-3}+\dfrac{x^2+3x}{2x+3}\left(\dfrac{x}{x^2-9}-\dfrac{x+3}{x\left(x-3\right)}\right)\)

\(=\dfrac{x^2-6}{x-3}+\dfrac{x\left(x+3\right)}{2x+3}\cdot\left(\dfrac{x}{\left(x-3\right)\left(x+3\right)}-\dfrac{x+3}{x\left(x-3\right)}\right)\)

\(=\dfrac{x^2-6}{x-3}+\dfrac{x\left(x+3\right)}{2x+3}\cdot\dfrac{x^2-\left(x+3\right)^2}{x\left(x-3\right)\left(x+3\right)}\)

\(=\dfrac{x^2-6}{x-3}+\dfrac{x^2-x^2-6x-9}{\left(2x+3\right)\left(x-3\right)}\)

\(=\dfrac{x^2-6}{x-3}-\dfrac{3}{x-3}=\dfrac{x^2-9}{x-3}=x+3\)

Gọi vận tốc thật của thuyền là x(km/h)

(ĐK: x>10)

Vận tốc lúc đi là x+10(km/h)

Vận tốc lúc về là x-10(km/h)

Độ dài quãng đường lúc đi và lúc về là bằng nhau nên ta có:

4(x+10)=5(x-10)

=>5x-50=4x+40

=>x=90(nhận)

Vậy: Khoảng cách từ A đến B là \(4\left(90+10\right)=400\left(km\right)\)

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có

\(\widehat{ABC}\) chung

Do đó: ΔABC~ΔHBA

b: XétΔHBA vuông tại H và ΔHAC vuông tại H có

\(\widehat{HBA}=\widehat{HAC}\left(=90^0-\widehat{C}\right)\)

Do đó: ΔHBA~ΔHAC

=>\(\dfrac{HB}{HA}=\dfrac{HA}{HC}\)

=>\(HB\cdot HC=HA^2\)

c: Xét tứ giác ADHE có \(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)

nên ADHE là hình chữ nhật

=>\(\widehat{AED}=\widehat{AHD}\)

mà \(\widehat{AHD}=\widehat{ABC}\left(=90^0-\widehat{HAB}\right)\)

nên \(\widehat{AED}=\widehat{ABC}\)

ΔABC vuông tại A

mà AM là đường trung tuyến

nên MA=MC

=>\(\widehat{MAC}=\widehat{ACB}\)

\(\widehat{MAC}+\widehat{AED}=\widehat{ABC}+\widehat{ACB}=90^0\)

=>DE\(\perp\)AM

\(\dfrac{x^2+x+1}{x+1}+\dfrac{x^2+2x+2}{x+2}-\dfrac{x^2+3x+3}{x+3}-\dfrac{x^2+4x+4}{x+4}=0\)

=>\(\dfrac{x\left(x+1\right)+1}{x+1}+\dfrac{x\left(x+2\right)+2}{x+2}-\dfrac{x\left(x+3\right)+3}{x+3}-\dfrac{x\left(x+4\right)+4}{x+4}=0\)

=>\(x+x-x-x+\dfrac{1}{x+1}+\dfrac{2}{x+2}-\dfrac{3}{x+3}-\dfrac{4}{x+4}=0\)

=>\(\left(\dfrac{1}{x+1}-1\right)+\left(\dfrac{2}{x+2}-1\right)-\left(\dfrac{3}{x+3}-1\right)-\left(\dfrac{4}{x+4}-1\right)=0\)

=>\(\dfrac{-x}{x+1}+\dfrac{-x}{x+2}-\dfrac{-x}{x+3}-\dfrac{-x}{x+4}=0\)

=>x=0

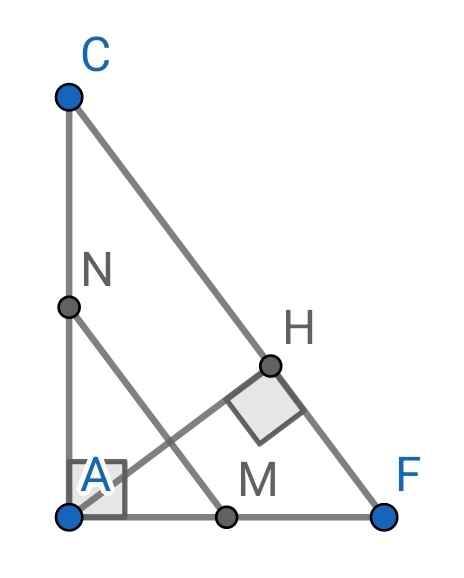
a) Sửa đề: Chứng minh MN là đường trung bình của ∆AFC

Do M là trung điểm của AF (gt)

N là trung điểm của AC (gt)

⇒ MN là đường trung bình của ∆AFC

b) Xét hai tam giác vuông: ∆AFC và ∆HFA có:

∠F chung

⇒ ∆AFC ∽ ∆HFA (g-g)

c) Xét hai tam giác vuông: ∆AHC và ∆FHA có:

∠ACH = ∠FAH (cùng phụ ∠AFC)

⇒ ∆AHC ∽ ∆FHA (g-g)

⇒ AH/HF = HC/AH

⇒ AH² = HF.HC