11/3 - 5/6 + 4/3 + 6 - 7/6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề thi đánh giá năng lực

Gọi độ dài 2 cạnh còn lại của tam giác là x và y
\(\Rightarrow x+y+6=16\Rightarrow x+y=10\)
\(S=\sqrt{8\left(8-6\right)\left(8-x\right)\left(8-y\right)}=4\sqrt{\left(8-x\right)\left(8-y\right)}\le2\left(8-x+8-y\right)=2.6=12\)
\(S_{max}=12\) khi \(\left\{{}\begin{matrix}x+y=10\\8-x=8-y\end{matrix}\right.\) \(\Rightarrow x=y=5\)


Bạn có thể ghi rõ đạo hàm \(f'\left(x\right)\) không? Căn thức đến chỗ nào vậy?


\(\overrightarrow{AB}=\left(-1;1;-5\right)\Rightarrow AB=3\sqrt{3}\)
Do D thuộc Ox nên tọa độ có dạng: \(D\left(a;0;0\right)\)
\(\Rightarrow\overrightarrow{AD}=\left(a-5;1;-6\right)\Rightarrow AD=\sqrt{\left(a-5\right)^2+37}\)
\(\Rightarrow\sqrt{\left(a-5\right)^2+37}=6\sqrt{3}\)
\(\Rightarrow\left(a-5\right)^2=71\Rightarrow\left[{}\begin{matrix}a=5+\sqrt{71}\\a=5-\sqrt{71}< 0\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow a^2+b+c=\left(5+\sqrt{71}\right)^2+0+0=96+10\sqrt{71}\)

hàm số \(y=x^0\text{ cũng chính là đường thẳng }y=1\) đây là một đường thẳng vuông góc với trục Oy tại điểm (0,1) thôi
còn hàm \(y=\frac{1}{x}\Rightarrow y'=-\frac{1}{x^2}< 0\forall x\) nên hàm số nghịch biến trên R.
Đồ thị hàm số

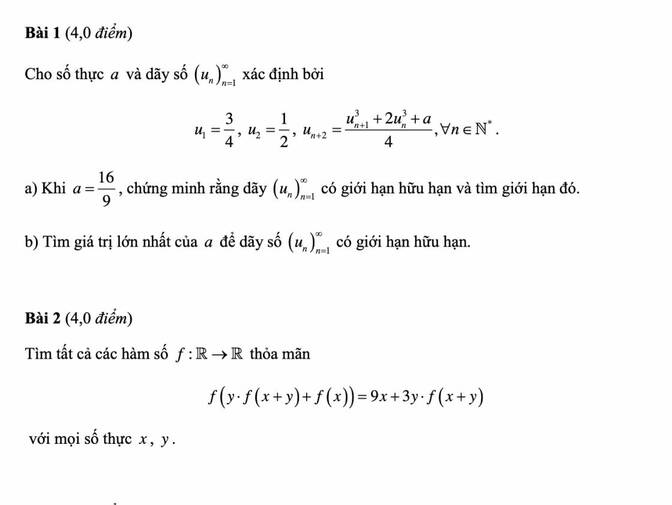

kết quả : 9
11/3 - 5/6 + 4/3 + 6 - 7/6
= 11/3 + 4/3 - 5/6 - 7/6 + 6
= (11/3 + 4/3) - (5/6 + 7/6) + 6
= 15/3 - 12/6 + 6
= 5 - 2 + 6
= 9