Câu 18. Nếu -30m biểu diễn độ sâu 30m dưới mực nước biển thì +20m biểu diễn độ cao là: A. - 40m dưới mực nước biển B. 20m dưới mực nước biển C. - 20m trên mực nước biển D. 20m trên mực nước biển
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


TH1: m=-2
BPT sẽ trở thành:
\(\left(-2+2\right)x^2-2\left(-2+2\right)x+1+3\cdot\left(-2\right)< =0\)
=>-5<=0(đúng)
=>Nhận
TH2: m<>-2
\(\text{Δ}=\left[-2\left(m+2\right)\right]^2-4\left(m+2\right)\left(3m+1\right)\)
\(=4\left(m^2+4m+4\right)-4\left(3m^2+7m+2\right)\)
\(=4\left(m^2+4m+4-3m^2-7m-2\right)=4\left(-2m^2-3m+2\right)\)
Để BPT luôn đúng với mọi x thực thì
\(\left\{{}\begin{matrix}\text{Δ}< =0\\m+2< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4\left(-2m^2-3m+2\right)< =0\\m< -2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2m^2-3m+2< =0\\m< -2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2m^2+3m-2>=0\\m< -2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2m^2+4m-m-2>=0\\m< -2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(m+2\right)\left(2m-1\right)>=0\\m< -2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}m>=\dfrac{1}{2}\\m< =-2\end{matrix}\right.\\m< -2\end{matrix}\right.\Leftrightarrow m< -2\)
Vậy: m<=-2

\(\dfrac{\left(x^2+8x+7\right)\left(x+3\right)\left(x+5\right)+15}{x^3+8x^2+10x}\)
\(=\dfrac{\left(x^2+8x+7\right)\left(x^2+8x+15\right)+15}{x\left(x^2+8x+10\right)}\)
\(=\dfrac{\left(x^2+8x\right)^2+22\left(x^2+8x\right)+105+15}{x\left(x^2+8x+10\right)}\)
\(=\dfrac{\left(x^2+8x\right)^2+22\left(x^2+8x\right)+120}{x\left(x^2+8x+10\right)}=\dfrac{\left(x^2+8x+10\right)\left(x^2+8x+12\right)}{x\left(x^2+8x+10\right)}\)
\(=\dfrac{x^2+8x+12}{x}\)
Olm chào em, em cần làm gì với biểu thức này?

3\(x\) = 5y; \(x+y=40\)
3\(x\) = 5y suy ra: \(x=\frac53\)y thay vào \(x+y=40\) ta được:
\(\frac53y+y=40\)
8y = 120
y = \(\frac{120}{8}\)
y = 15 thay vào \(x=\frac53y\) ta được \(x=\) \(\frac53\times15=25\)
Vậy (\(x;y\) ) = (25; 15)

Giải:
Chiều cao của tam giác là:
5 x 2 : 2 = 5(m)
Diện tích tam giác là:
6 x 5 : 2 =15 (m\(^2\))
Đáp số: 15m\(^2\)

b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{1,1}=\dfrac{y}{1,3}=\dfrac{z}{1,4}=\dfrac{2x-y}{2\cdot1,1-1,3}=\dfrac{5.5}{0.9}=\dfrac{55}{9}\)
=>\(\left\{{}\begin{matrix}x=\dfrac{55}{9}\cdot1,1=\dfrac{121}{18}\\y=\dfrac{55}{9}\cdot1,3=\dfrac{143}{18}\\z=\dfrac{55}{9}\cdot1,4=\dfrac{77}{9}\end{matrix}\right.\)
c:
x-y+100=z
=>x-y-z=-100
\(\dfrac{x}{4}=\dfrac{y}{3}\)
=>\(\dfrac{x}{20}=\dfrac{y}{15}\left(1\right)\)
\(\dfrac{y}{5}=\dfrac{z}{3}\)
=>\(\dfrac{y}{15}=\dfrac{z}{9}\left(2\right)\)
Từ (1),(2) suy ra \(\dfrac{x}{20}=\dfrac{y}{15}=\dfrac{z}{9}\)
mà x-y-z=-100
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{20}=\dfrac{y}{15}=\dfrac{z}{9}=\dfrac{x-y-z}{20-15-9}=\dfrac{-100}{-4}=25\)
=>\(\left\{{}\begin{matrix}x=25\cdot20=500\\y=25\cdot15=375\\z=25\cdot9=225\end{matrix}\right.\)
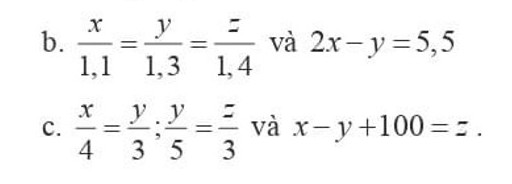
D. 20 m trên mực nước biển
Nếu -30 biểu diễn độ sâu 30m dưới mặt nước biển, thì +20 biểu diễn độ cao 20m trên mặt nước biển, tức là một vị trí cao hơn mặt nước biển 20m.
Bài này chọn câu D nha