Cho ba chữ số 5; 4 và 1. Tổng tất cả các số có ba chữ số tạo thành từ cả ba chữ số trên và mỗi chữ số xuất hiện một lần bằng bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 6:
\(A=ax+bx+3ay+3by\)
\(=x\left(a+b\right)+3y\left(a+b\right)\)
\(=\left(a+b\right)\left(x+3y\right)=5\cdot7=35\)
Bài 7:
a: \(\left(2x-4\right)^2>=0\forall x\)
\(\left(3y-9\right)^4>=0\forall y\)
Do đó: \(\left(2x-4\right)^2+\left(3y-9\right)^4>=0\forall x,y\)
mà \(\left(2x-4\right)^2+\left(3y-9\right)^4< =0\forall x,y\)
nên \(\left\{{}\begin{matrix}2x-4=0\\3y-9=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\)
b; (\(x^3\) - 1)(\(x^3\) - 10)(\(x^3\) - 30)(\(x^3\) - 70) < 0
Đặt \(x^3\) = t
Khi đó: T = (t - 1)(t - 10)(t - 30)(t - 70) < 0
Lập bảng xét dấu ta có:
| t | 1 10 30 70 |
| t - 1 | - 0 + + + + |
| t - 10 | - - 0 + + + |
| t - 30 | - - - 0 + + |
| t - 70 | - - - - 0 + |
| T = (t - 1).(t - 10).(t - 30).(t - 70) | + 0 - 0 + 0 - 0 + |
Theo bảng trên ta có:
1 < t < 10 hoặc 30 < t < 70
⇒ 1 < \(x^3\) - 1 < 10 ⇒ 2 < \(x^3\) < 11
Vì \(x\) nguyên nên \(x\)3 = 8 ⇒ \(x^3\) = 23 ⇒ \(x=2\)
30 < t < 70
30 < \(x^3\) - 1 < 70
31 < \(x^3\) < 71
Vì \(x\) nguyên nên \(x^3\) = 64
⇒ \(x^3\) = 43 ⇒ \(x\) = 4
Vậy \(x\) \(\in\) {2; 4}

Giải:
Gọi số tự nhiên nhỏ nhất cần tìm là \(x\); \(x\in\) N thì theo bài ra ta có:
Số thứ hai là: \(x\) + 1
Số thứ ba là: \(x+1+1\) = \(x\) + 2
Theo bài ra ta có: \(x\) + \(x\) + 1 + \(x\) + 2 = 183
(\(x\) + \(x\) + \(x\)) + (1 + 2) = 183
3\(x\) + 3 = 183
3\(x\) = 183 - 3
3\(x\) = 180
\(x\) = 180 : 3
\(x\) = 60
Vậy số tự nhiên nhỏ nhất thỏa mãn đề bài là: 60
Trung bình cộng của ba số là : 183:3=61
Vì trung bình cộng của ba số là số thứ hai.
Số nhỏ nhất là:61-1=60
Đáp số:60.

\(A=5+5^2+5^3+\dots+5^{200}\\5A=5^2+5^3+5^4+\dots+5^{201}\\5A-A=(5^2+5^3+5^4+\dots+5^{201})-(5+5^2+5^3+\dots+5^{200})\\4A=5^{201}-5\\\Rightarrow A=\frac{5^{201}-5}{4}\)
A = 5 + 5² + 5³ + ... + 5²⁰⁰
⇒ 5A = 5² + 5³ + 5⁴ + ... + 5²⁰¹
⇒ 4A = 5A - A
= (5² + 5³ + 5⁴ + ... + 5²⁰¹) - (5 + 5² + 5³ + ... + 5²⁰⁰)
= 5²⁰¹ - 5
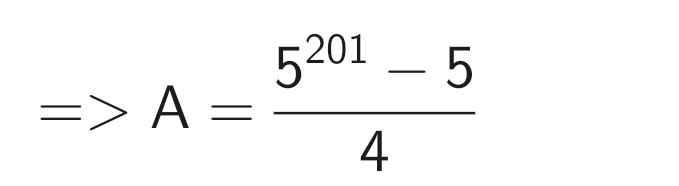

Do 17 là số bị chia và số dư là 5 nên:
ab = 17 - 5 = 12
Lại có:
12 = 1.12 = 2.6 = 3.4
Mà số dư là 5 nên a = 6 hoặc a = 12
Khi đó b = 2 hoặc b = 1
Vậy ta có các cặp số (a; b) thỏa mãn:
(12; 1); (6; 2)

Đây là dạng toán nâng cao lập số theo điều kiện cho trước,
Giải:
Vì xóa đi chữ số đầu của số X thì số đó giảm đi 2000 đơn vị. Vậy chữ số bị xóa là chữ số ở vị trí hàng nghìn và đó là chữ số 2.
Vì chữ số 2 là số đứng đầu, lại đứng ở vị trí hàng nghìn của số X nên số X là số có bốn chữ số.
Vì số X là số có các chữ số giống nhau nên số X là:
2222
Đáp số: 2222

Đề bị lỗi, em có thể viết bằng công thức toán học để mọi người hiểu đúng đề bài em nhé.

a: Để A là số nguyên thì \(n-5⋮n+1\)
=>\(n+1-6⋮n+1\)
=>\(-6⋮n+1\)
=>\(n+1\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
=>\(n\in\left\{0;-2;1;-3;2;-4;5;-7\right\}\)
Khi n=0 thì \(A=\dfrac{0-5}{0+1}=-5< 0\)(nhận)
Khi n=-2 thì \(A=\dfrac{-2-5}{-2+1}=\dfrac{-7}{-1}=7>0\left(loại\right)\)
Khi n=1 thì \(A=\dfrac{1-5}{1+1}=\dfrac{-4}{2}=-2< 0\)(nhận)
Khi n=-3 thì \(A=\dfrac{-3-5}{-3+1}=\dfrac{-8}{-2}=4>0\)(loại)
Khi n=2 thì \(A=\dfrac{2-5}{2+1}=\dfrac{-3}{3}=-1< 0\)(nhận)
Khi n=-4 thì \(A=\dfrac{-4-5}{-4+1}=\dfrac{-9}{-3}=3>0\left(loại\right)\)
Khi n=5 thì \(A=\dfrac{5-5}{5+1}=0\left(loại\right)\)
Khi n=-7 thì \(A=\dfrac{-7-5}{-7+1}=\dfrac{-12}{-6}=2>0\left(loại\right)\)
b: \(A=\dfrac{n-5}{n+1}=\dfrac{n+1-6}{n+1}=1-\dfrac{6}{n+1}\)
Để A có giá trị nhỏ nhất thì \(-\dfrac{6}{n+1}\) nhỏ nhất
=>\(\dfrac{6}{n+1}\) lớn nhất
=>n+1=1
=>n=0
Để A có giá trị lớn nhất thì \(\dfrac{6}{n+1}\) nhỏ nhất
=>n+1=-1
=>n=-2
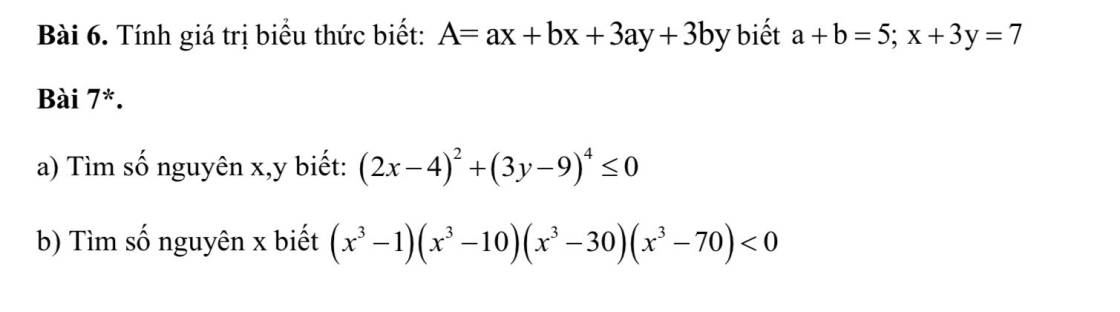

mik nghĩ là 9:)))
có 3 lựa chọn hàng trăm, mỗi lựa chọn hàng trăm có 2 lựa chọn hàng chục, mỗi lựa chọn hàng chục có 1 lựa chọn hàng đơn vị.
vậy cố tất cả số số là:3x2x1=6( số)