Gọi ba số tự nhiên liên tiếp lần lượt là x;x+1;x+2

Cộng ba tích, mỗi tích của tích của hai trong ba số trên thì được 26 nên ta có:

\(x\left(x+1\right)+\left(x+1\right)\left(x+2\right)+x\left(x+2\right)=26\)

=>\(x^2+x+x^2+3x+2+x^2+2x=26\)

=>\(3x^2+6x+2-26=0\)

=>\(3x^2+6x-24=0\)

=>\(x^2+2x-8=0\)

=>(x+4)(x-2)=0

=>\(\left[{}\begin{matrix}x=-4\left(loại\right)\\x=2\left(nhận\right)\end{matrix}\right.\)

Vậy: Ba số liên tiếp cần tìm là 2;3;4

                         Giải:

Ba số tự nhiên liên tiếp có dạng: n; n + 1;  n + 2 (n \(\in\)  N*)

Tích của số thứ nhất và số thứ hai là: n.(n + 1)

Tích của số thứ nhất và số thứ ba là: n.(n + 2) 

Tích của số thứ hai và số thứ ba là: (n + 1).(n + 2)

Theo bài ra ta có:

 n(n + 1) + n(n+2) + (n + 1)(n + 2) = 26

 n² + n + n² + 2n + n² + n + 2n + 2  = 26

 3n² + 6n + 2  - 26 = 0

3n² + 6n -  24 = 0

3n² - 12 + 6n - 12= 0

(3n² - 12) + (6n - 12) = 0

3(n² - 4) + 6(n - 2) = 0

3(n - 2)(n + 2) + 6(n - 2) = 0

(n - 2)(3n + 6  + 6) = 0

 (n - 2)(3n + 12) = 0

\(\left[{}\begin{matrix}n-2=0\\3n+12=0\end{matrix}\right.\)

\(\left[{}\begin{matrix}n=2\\n=-4\end{matrix}\right.\)

n = - \(4\) (loại)

Vậy n = 2, nên số thứ nhất là 2 

Kết luận: Ba số tự nhiên liên tiếp đó là:   2; 3; 4

1: Xét ΔPMN có AB//MN

nên \(\dfrac{AB}{MN}=\dfrac{PA}{PM}\)

=>\(\dfrac{AB}{MN}=\dfrac{3}{7}\)

mà MN-AB=8

nên \(MN=8:\left(7-3\right)\cdot7=8:4\cdot7=14\left(cm\right)\)

=>AB=14-8=6(cm)

2:

a: Xét ΔABD có AE là phân giác

nên \(\dfrac{BE}{ED}=\dfrac{BA}{AD}\)

Xét ΔBAC có BF là phân giác

nên \(\dfrac{FA}{FC}=\dfrac{BA}{BC}=\dfrac{BA}{AD}\)

=>\(\dfrac{BE}{ED}=\dfrac{FA}{FC}\)

b:

Ta có: ABCD là hình bình hành

=>AC cắt BD tại trung điểm của mỗi đường

=>O là trung điểm chung của AC và BD

 \(\dfrac{BE}{ED}=\dfrac{FA}{FC}\)

=>\(\dfrac{BE}{ED}+1=\dfrac{FA}{FC}+1\)

=>\(\dfrac{BD}{ED}=\dfrac{AC}{FC}\)

mà BD=2OD và AC=2OC

nên \(\dfrac{2OD}{ED}=\dfrac{2OC}{FC}\)

=>\(\dfrac{OD}{ED}=\dfrac{OC}{FC}\)

Xét ΔODC có \(\dfrac{OD}{ED}=\dfrac{OC}{FC}\)

nên EF//CD

a: Đặt (d): y=ax+b 

Theo đồ thị, ta sẽ thấy: (d) đi qua A(6;0) và B(9;120)

Thay x=6 và y=0 vào y=ax+b, ta được:

\(a\cdot6+b=0\)

=>6a+b=0(1)

Thay x=9 và y=120 vào y=ax+b, ta được:

\(a\cdot9+b=120\)

=>9a+b=120(2)

Từ (1) và (2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}9a+b=120\\6a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9a+b-6a-b=120\\6a+b=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}3a=120\\b=-6a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=40\\b=-240\end{matrix}\right.\)

b: a=40; b=-240

=>y=40x-240

Thay x=8 vào y=40x-240, ta được:

\(y=40\cdot8-240=80\left(km\right)\)

=>Ô tô còn cách B 120-80=40km

a: Vì đường thẳng y=ax+b song song với đường thẳng y=3x-7 nên \(\left\{{}\begin{matrix}a=3\\b\ne-7\end{matrix}\right.\)

=>y=3x+b

Thay x=1 và y=2 vào y=3x+b, ta được:

\(b+3\cdot1=2\)

=>b+3=2

=>b=-1

Vậy: y=3x-1

b: Tọa độ giao điểm của (d1) và (d2) là:

\(\left\{{}\begin{matrix}2x-7=-3x+3\\y=2x-7\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}5x=10\\y=2x-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2\cdot2-7=-3\end{matrix}\right.\)

Thay x=2 và y=-3 vào y=ax+b, ta được:

\(a\cdot2+b=-3\)

=>2a+b=-3(1)

Thay x=-2 và y=5 vào y=ax+b, ta được:

\(a\cdot\left(-2\right)+b=5\)

=>-2a+b=5(2)

Từ (1) và (2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}2a+b=-3\\-2a+b=5\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2a+b-2a+b=-3+5\\2a+b=-3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2b=2\\2a=-3-b\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}b=1\\2a=-3-1=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=1\end{matrix}\right.\)

a: 

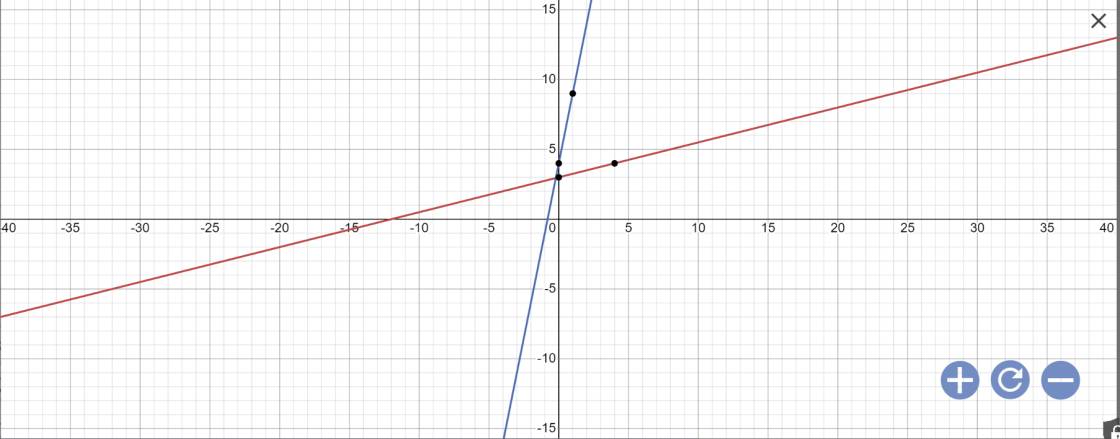
b: Tọa độ giao điểm của d1 với trục Ox là:

\(\left\{{}\begin{matrix}y=0\\\dfrac{1}{4}x+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\\dfrac{x}{4}=-3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=-12\\y=0\end{matrix}\right.\)

Vậy: (d1) giao Ox tại A(-12;0)

Tọa độ giao điểm của (d1) với trục Oy là:

\(\left\{{}\begin{matrix}x=0\\y=\dfrac{1}{4}x+3=\dfrac{1}{4}\cdot0+3=3\end{matrix}\right.\)

vậy: (d1) giao Oy tại B(0;3)

a:

ĐKXĐ: \(x\ne0;y\ne0\)

 \(\dfrac{\dfrac{1}{x}+\dfrac{1}{y}}{\dfrac{1}{x}-\dfrac{1}{y}}=\dfrac{x+y}{xy}:\dfrac{x-y}{xy}=\dfrac{x+y}{xy}\cdot\dfrac{xy}{x-y}=\dfrac{x+y}{x-y}\)

b:

ĐKXĐ: \(x\notin\left\{0;1;-1\right\}\)

 \(\dfrac{\dfrac{x}{x+1}-\dfrac{x-1}{x}}{\dfrac{x}{x-1}-\dfrac{x+1}{x}}\)

\(=\left(\dfrac{x^2-\left(x-1\right)\left(x+1\right)}{x\left(x+1\right)}\right):\dfrac{x^2-\left(x-1\right)\left(x+1\right)}{x\left(x-1\right)}\)

\(=\dfrac{x^2-x^2+1}{x\cdot\left(x+1\right)}\cdot\dfrac{x\left(x-1\right)}{x^2-x^2+1}\)

\(=\dfrac{x-1}{x+1}\)

c:

ĐKXĐ: \(x\ne-1\)

 \(1-\dfrac{x}{1-\dfrac{x}{x+1}}\)

\(=1-\dfrac{x}{\dfrac{x+1-x}{x+1}}\)

\(=1-\dfrac{x}{\dfrac{1}{x+1}}\)

\(=1-x\left(x+1\right)=1-x^2-x\)

\(B=\dfrac{-\left(2x^2+3\right)+2x^2+x+5}{2x^2+3}=-1+\dfrac{2\left(x+\dfrac{1}{4}\right)^2+\dfrac{39}{8}}{2x^2+3}>-1\)

\(B=\dfrac{2x^2+3-2x^2+x-1}{2x^2+3}=1-\dfrac{2\left(x-\dfrac{1}{4}\right)^2+\dfrac{7}{8}}{2x^2+3}< 1\)

\(\Rightarrow-1< B< 1\)

Mà B nguyên \(\Rightarrow B=0\)

\(\Rightarrow x+2=0\Rightarrow x=-2\)