Tích sau có bao nhiêu chữ số giống nhau ở tận cùng bên phải ?? 1 x 2 x 3 x 4 x ....x 99 x 100
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{34}{62}+a=\dfrac{1}{3}\\ =>\dfrac{17}{31}+a=\dfrac{1}{3}\\ =>a=\dfrac{1}{3}-\dfrac{17}{31}\\ =>a=\dfrac{31}{93}-\dfrac{51}{93}\\ =>a==\dfrac{-20}{93}\)

Chiều rộng hình chữ nhật là \(8:2=4\left(m\right)\)
Diện tích hình chữ nhật là 8x4=32(m2)=3200(dm2)
diện tích 1 viên gạch là 4x4=16(dm2)
Số viên gạch cần dùng là 3200:16=200(viên)

Gọi chiều dài là a => chiều rộng = a-4
Theo bài ra: a+(a-4)=80
<=> 2a = 84
=> a = 42
=> chiều rộng = a-4 = 42-4 = 38
Diện tích tấm màn là: 38x42= 1596 m2

\(A=\dfrac{7}{19\cdot31}+\dfrac{5}{19\cdot43}+\dfrac{3}{23\cdot43}+\dfrac{11}{23\cdot57}+\dfrac{19}{38\cdot57}\)
\(=2\left(\dfrac{7}{31\cdot38}+\dfrac{5}{38\cdot43}+\dfrac{3}{43\cdot46}+\dfrac{11}{46\cdot57}+\dfrac{19}{57\cdot76}\right)\)
\(=2\left(\dfrac{1}{31}-\dfrac{1}{38}+\dfrac{1}{38}-\dfrac{1}{43}+\dfrac{1}{43}-\dfrac{1}{46}+\dfrac{1}{46}-\dfrac{1}{57}+\dfrac{1}{57}-\dfrac{1}{76}\right)\)
\(=2\left(\dfrac{1}{31}-\dfrac{1}{76}\right)=2\cdot\dfrac{45}{31\cdot76}=\dfrac{45}{1178}\)

Hiệu của số thứ 2 mới và số thứ 2 cũ bằng hiệu giữa tổng mới và tổng cũ
Hiệu của số thứ 2 mới và số thứ 2 cũ là:
`580 - 420 = 160 `
Ta có sơ đồ:
Số thứ 2 cũ: `1` phần
Số thứu 2 mới: `3` phần
Hiệu số phần bằng nhau là:
`3 - 1 = 2` (phần)
Giá trị 1 phần là:
`160 : 2 = 80`
Số thứ hai cũ là:
`80 ` x `1 = 80`
Số thứ nhất là:
`420 - 80 = 340`
Đáp số: .....
2 lần số thứ hai là 580-420=160
Số thứ hai là 160:2=80
Số thứ nhất là 420-80=340


x:6+17568=30876
=>x:6=30876-17568=13308
=>\(x=13308\times6=79848\)
\(X:6+17568=30876\)
\(X:6=30876-17568\)
\(X:6=13308\)
\(X=13308.6\)
\(X=79848\)

\(F=\dfrac{\dfrac{2010}{1}+\dfrac{2009}{2}+...+\dfrac{1}{2010}+2010}{1+\dfrac{1}{2}+...+\dfrac{1}{2010}}\)
\(=\dfrac{\left(\dfrac{2010}{1}+1\right)+\left(\dfrac{2009}{2}+1\right)+...+\left(\dfrac{1}{2010}+1\right)}{1+\dfrac{1}{2}+...+\dfrac{1}{2010}}\)
\(=\dfrac{\dfrac{2011}{1}+\dfrac{2011}{2}+...+\dfrac{2011}{2010}}{1+\dfrac{1}{2}+...+\dfrac{1}{2010}}=2011\)
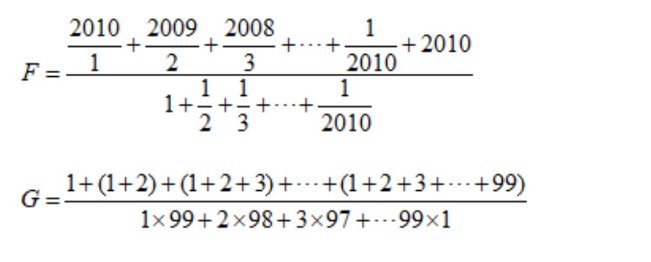 Gíup mình nha
Gíup mình nha