Câu 1: B

Câu 2: A

Câu 3: B

Câu 4: C

Câu 5: D

Câu 6: A

Câu 7: \(\dfrac{x+2}{6}=\dfrac{-15}{2}\)

=>\(\dfrac{x+2}{6}=\dfrac{-45}{6}\)

=>x+2=-45

=>x=-47

=>Chọn C

Câu 8: B

Câu 9: C

Câu 10: A

Câu 11: \(x\cdot\dfrac{3}{4}=\dfrac{7}{8}\)

=>\(x=\dfrac{7}{8}:\dfrac{3}{4}=\dfrac{7}{8}\cdot\dfrac{4}{3}=\dfrac{28}{24}=\dfrac{7}{6}\)

=>Chọn C

Câu 12: C

Câu 13: D

Câu 14; C

Câu 15: A

Câu 16: D

II: Tự luận:

Bài 2:

a: \(3\dfrac{1}{3}x+16=13,25\)

=>\(x\cdot\dfrac{10}{3}=13,25-16=-2,75\)

=>\(x=-\dfrac{11}{4}:\dfrac{10}{3}=-\dfrac{11}{4}\cdot\dfrac{3}{10}=\dfrac{-33}{40}\)

b: \(x-43=\left(57-x\right)-50\)

=>x-43=7-x

=>2x=50

=>x=25

Các bn ơi,giúp mk với mk đag cần gấp lắm!!!!

diện tích trồng cây ăn quả là:

\(1200\times\dfrac{2}{3}=800\left(m^2\right)\)

diện tích trồng hoa là:

\(60:\dfrac{5}{6}=72\left(m^2\right)\)

diện tích trồng rau là:

\(1200-72-800=328\left(m^2\right)\)

tỉ số phần trăm giữa diện tích trồng hoa và diện tích trồng rau là:

72:328\(\times\)100%\(\approx\)22%

\(\overline{a,b}-\overline{0,ab}=4,05\)

=>\(\overline{a,b}-\overline{a,b}\times0,1=4,05\)

=>\(0,9\times\overline{a,b}=4,05\)

=>\(\overline{a,b}=4,05:0,9=4,5\)

\(\overline{a,b}\) - \(\overline{0,ab}\) = 4,05

\(\overline{a,b}\) x 1 - \(\overline{a,b}\)  x 0,1 = 4,05

\(\overline{a,b}\) x (1 - 0,1) = 4,05

\(\overline{a,b}\) x 0,9 = 4,05

\(\overline{a,b}\)         = 4,05 : 0,9

\(\overline{a,b}\)         = 4,5

a: \(\widehat{AOC}+\widehat{AOB}=180^0\)(hai góc kề bù)

=>\(\widehat{AOC}+124^0=180^0\)

=>\(\widehat{AOC}=56^0\)

b: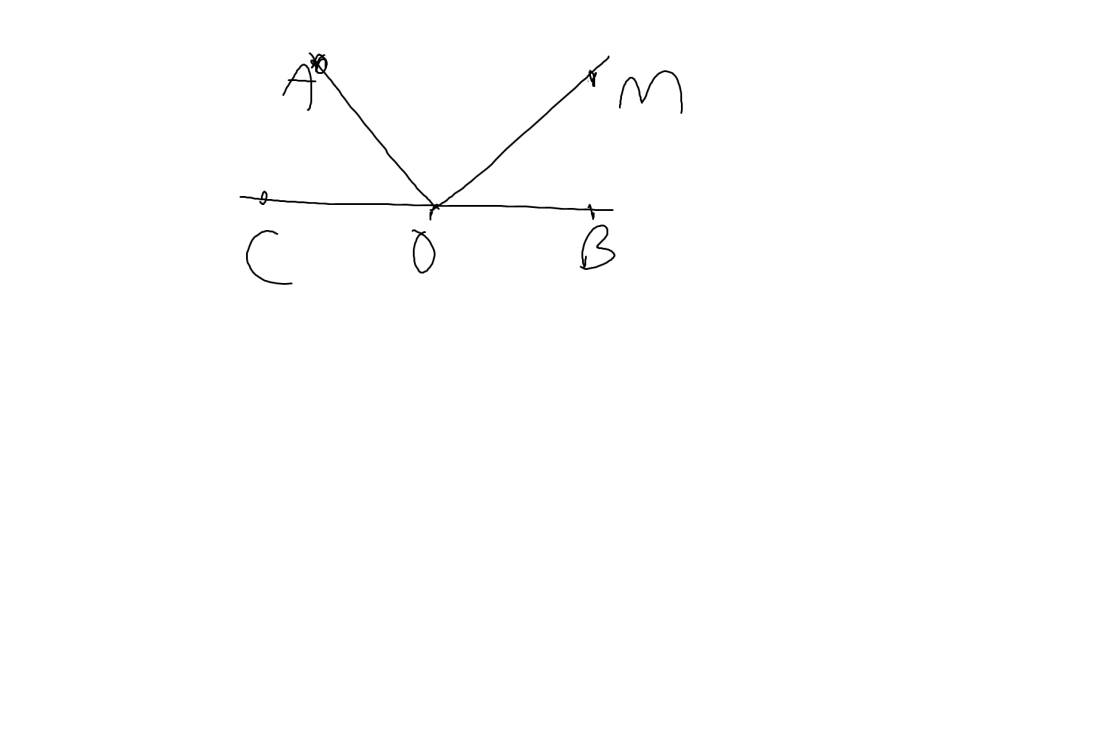 

Ta biết:\(\dfrac{11}{17}\)<\(\dfrac{a}{b}< \dfrac{23}{29}\) và \(8b-9a=31\)(\(a,b\in N\))

\(\Rightarrow b=\dfrac{31+9a}{8}=\dfrac{32-1+8a+a}{8}=\left[\left(4+a\right)+\dfrac{a-1}{8}\right]\in N\)

⇒\(\dfrac{a-1}{8}\in N\)

\(\Leftrightarrow\left(a-1\right)⋮8\Rightarrow a=8k++1\)

khi đó\(b=\dfrac{31+9.\left(8k+1\right)}{8}=9k+5\)⇒\(\dfrac{11}{17}< \dfrac{8k+1}{9k+5}< \dfrac{23}{29}\)

11.(9k+5)<17.(8k+1)⇔k>129.(8k+1)<23.(9k+5)⇔k<4⇒1<k<4​

⇒kϵ{2;3}

k=2=>a=17

          b=23

k=3=>a=25

          b=32

kết luận:(a,b) là:(17,23);(25,32)

Số nguyên tố lẻ nhỏ nhất là số 3

=>a=3

Số chục là số nguyên tố chẵn

=>b=2

Số đơn vị là số nguyên tố duy nhất có tận cùng bằng 5

=>Hàng đơn vị là c=5

vậy: Số cần tìm là 325

giúp mình với ạ

Lời giải:

Giả sử (𝑎2+𝑏2,𝑎𝑏)>1(a2+b2,ab)>1. Khi đó, gọi 𝑝p là ước nguyên tố lớn nhất của (𝑎2+𝑏2,𝑎𝑏)(a2+b2,ab)

⇒𝑎2+𝑏2⋮𝑝;𝑎𝑏⋮𝑝⇒a2+b2⋮p;ab⋮p

Vì 𝑎𝑏⋮𝑝⇒𝑎⋮𝑝ab⋮p⇒a⋮p hoặc 𝑏⋮𝑝b⋮p

Nếu 𝑎⋮𝑝a⋮p. Kết hợp 𝑎2+𝑏2⋮𝑝⇒𝑏2⋮𝑝a2+b2⋮p⇒b2⋮p

⇒𝑏⋮𝑝⇒b⋮p

⇒𝑝=Ư𝐶(𝑎,𝑏)⇒p=ƯC(a,b) . Mà (𝑎,𝑏)=1(a,b)=1 nên vô lý 

Tương tự nếu 𝑏⋮𝑝b⋮p
Vậy điều giả sử là sai. Tức là (𝑎2+𝑏2,𝑎𝑏)=1(a2+b2,ab)=1

Số học sinh trung bình chiếm số 12 cả lớp là sao em?

B = \(\dfrac{-8}{2n-1}\) (n \(\in\) Z)

a; Tìm điều kiện của số nguyên n để B là phân số

B là phân số khi và chỉ khi 2n - 1 \(\ne\) 0 ⇒ n ≠ \(\dfrac{1}{2}\)

Vậy B là phân số với mọi giá trị của n \(\in\) Z

b; Tìm số nguyên n để B nguyên

B = \(\dfrac{-8}{2n-1}\) \(\in\) Z ⇔ 8 ⋮ 2n - 1

2n - 1 \(\in\) Ư(8) = {-8; -4; -2; -1; 1; 2; 4; 8}

Lập bảng ta có:

vì n thuộc z nên theo bảng trên ta có: n \(\in\){0; 1}

Kết luận với n \(\in\) {0; 1} thì biểu thức B =\(\dfrac{-8}{2n-1}\) là một só nguyên. 

nhanh giúp mk với