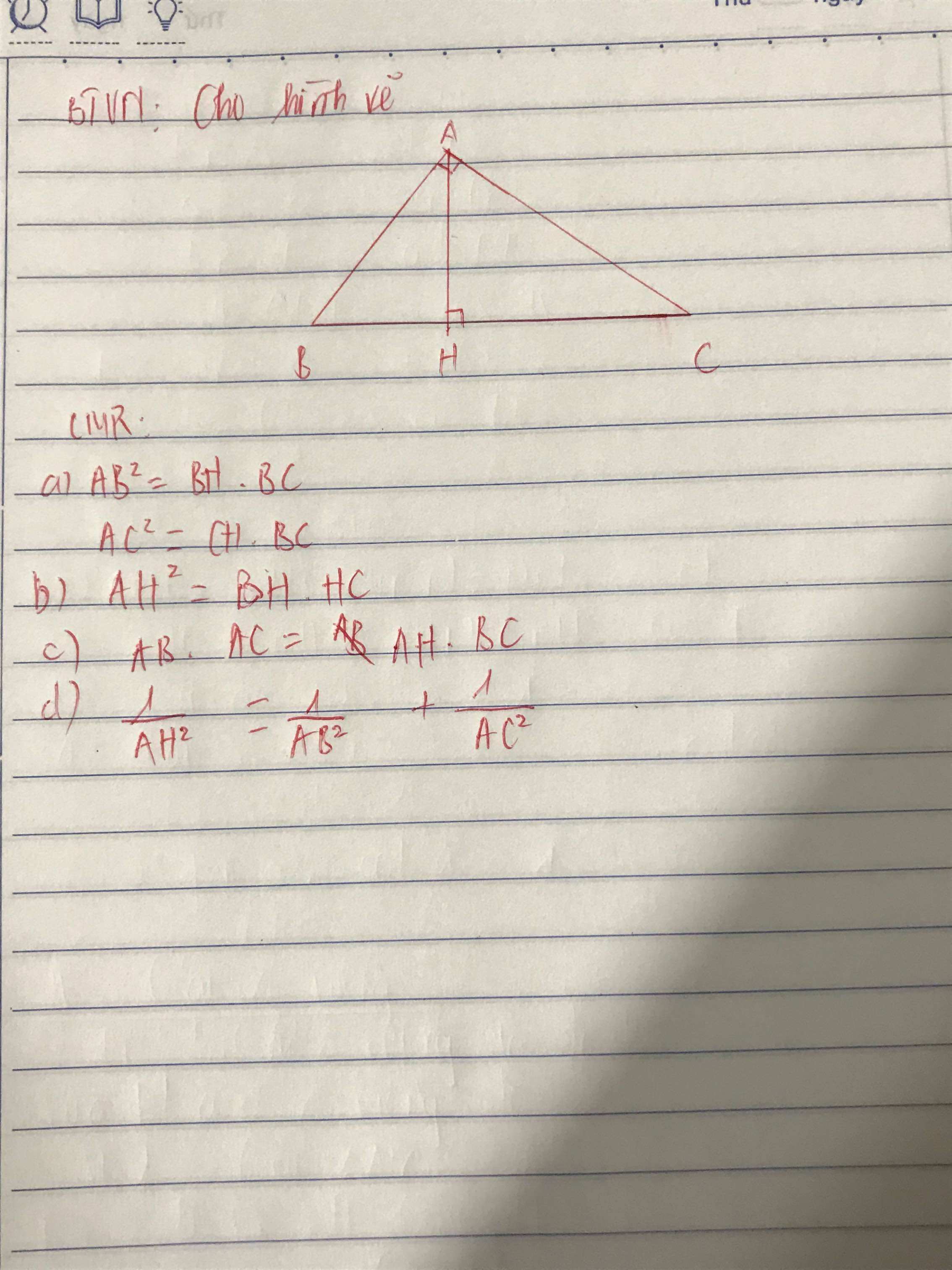a: Xét ΔBHA vuông tại H và ΔBAC vuông tại A có

\(\widehat{HBA}\) chung

Do đó: ΔBHA~ΔBAC
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)

=>\(BA^2=BH\cdot BC\)

Xét ΔCHA vuông tại H và ΔCAB vuông tại A có

\(\widehat{HCA}\) chung

Do đó: ΔCHA~ΔCAB

=>\(\dfrac{CH}{CA}=\dfrac{CA}{CB}\)

=>\(CH\cdot CB=CA^2\)

b: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có

\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)

Do đó: ΔHAB~ΔHCA

=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)

=>\(HA^2=HB\cdot HC\)

c: ΔCHA~ΔCAB

=>\(\dfrac{CA}{CB}=\dfrac{AH}{AB}\)

=>\(AB\cdot AC=AH\cdot BC\)

d: \(\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{AB^2+AC^2}{AB^2\cdot AC^2}=\dfrac{BC^2}{BH\cdot BC\cdot CH\cdot BC}=\dfrac{1}{BH\cdot CH}=\dfrac{1}{AH^2}\)

a, Xét tam giác AHB và tam giác CAB có

^AHB = ^CAB ; ^ABH _ chung 

Vậy tam giác AHB ~ tam giác CAB (g.g) 

\(\dfrac{AB}{BC}=\dfrac{HB}{AB}\Rightarrow AB^2=HB.BC\)

tương tự tam giác AHC ~ tam giác CAB 

\(\dfrac{AH}{AC}=\dfrac{AC}{BC}\Rightarrow AC^2=AH.BC\)

b, Xét tam giác AHB và tam giác CHA ta có 

^AHB = ^CHA ; ^ABH = ^CAH ( cùng phụ với ^BAH ) 

Vậy tam giác AHB ~ tam giác CHA (g.g) 

\(\dfrac{AH}{CH}=\dfrac{HB}{AH}\Rightarrow AH^2=HB.HC\)

c, \(S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}AH.BC\Rightarrow AB.AC=AH.BC\)

d, Ta có \(AH^2=BH.CH\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{BH.CH}=\dfrac{BC^2}{AB^2.AC^2}=\dfrac{AB^2+AC^2}{AB^2.AC^2}=\dfrac{1}{AC^2}+\dfrac{1}{AB^2}\)

1. 

a) các y ta có các giá trị công tác là: 1, 2, 3, 4, 5, 6, 7

Tần số của các giá trị là: 

Số năm công tác: 

1 có 6 y tá

2 có 5 y tá

3 có 5 y tá

4 có 7 y tá

5 có 9 y tá 

6 có 5 y tá 

7 có 2 y tá 

b) Phòng khám có tổng số:

6 + 5 + 5 + 7 + 9 + 5 + 2 = 39 (y tá) 

c) Số y tá đã công tác ở phòng khám ít nhất 3 năm là:

5 + 7 + 9 + 5 + 2 = 28 (y tá) 

Gọi chữ số hàng chục là: a 

Chữ số hàng đơn vị là: b

ĐK: \(a,b\in N,1\le a\le9;0\le b\le9\)

Ta có: b=4a (1)

Nếu thêm số 0 vào giữa 2 chữ số thì đc số hơn số cũ 180 nên ta có pt: 

\(\overline{a0b}-\overline{ab}=180\Leftrightarrow100a+b-10a-b=180\Leftrightarrow90a=180\Leftrightarrow a=2\) (tm)

=> b=4*2=8 (tm) 

Vậy số cần tìm là:  28

\(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\sqrt{\dfrac{216}{3}}\)

\(=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}-\sqrt{72}\)

\(=\dfrac{\sqrt{6}}{2}-6\sqrt{2}=\dfrac{\sqrt{6}-12}{2}\)

a:

ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne1\end{matrix}\right.\)

 Sửa đề: \(A=\sqrt{x}:\left(\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}+\dfrac{x+2}{x\sqrt{x}-1}\right)\)

\(=\sqrt{x}:\left(\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)-x-\sqrt{x}-1+x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right)\)

\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{x-1-\sqrt{x}+1}=\dfrac{\left(x-\sqrt{x}\right)\left(x+\sqrt{x}+1\right)}{x-\sqrt{x}}\)

\(=x+\sqrt{x}+1\)

b: Để A=7 thì \(x+\sqrt{x}+1=7\)

=>\(x+\sqrt{x}-6=0\)

=>\(\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)=0\)

=>\(\sqrt{x}-2=0\)(Vì \(\sqrt{x}+3>0\forall x\) thỏa mãn ĐKXĐ)

=>x=4(nhận)

Cảm ơn bn,may mà có bn

A được định nghĩa như thế nào hả bạn?

Nó là X+căn X +1/1=7/1 á bn mik tính mãi ko ra :((

Xét tam giác ABC vuông tại A

tanC = AB/AC \(\Rightarrow AC=\dfrac{AB}{tanC}=\dfrac{70}{tan35^0}\approx99,97m\)

Xét tam giác BDO vuông tại B 

Ta có ^BOD = ^DBO - ^BDO = 90⁰ - ^BDO 

Mà BD // AC => ^BDO = ^ACO ( do 2 góc này ở vị trí đồng vị ) 

Kẻ DH vuông AC tại H 

Ta có DH = AB = 3 cm 

Xét tam giác CHD vuông tại H 

\(sinC=\dfrac{HD}{CD}=\dfrac{3}{4}\Rightarrow\widehat{C}\approx48,59^0\)

\(\Rightarrow\widehat{BOD}=90^0-48,59^0\approx41^0\)

Các phương trình bậc nhất 2 ẩn là: `3x-y=3;x+2y=8;y+3y=11`

Hệ số a,b,c của các pt là: 

+) `3x-y=3` có `a=3; b=-1;c=3` 

+) `x+2y=8` có `a=1;b=2;c=8` 

+) `y+3x=11` có `a=3;b=1;c=11`