BÀI TỈ SỐ LƯỢNG GIÁC
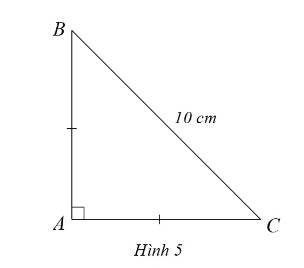
Cho ▲ABC vuông cân tại A, biết BC=10cm. Tính AB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
a: \(\left\{{}\begin{matrix}4x+y=2\\\dfrac{4}{3}x+\dfrac{1}{3}y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2-4x\\\dfrac{4}{3}x+\dfrac{1}{3}\left(2-4x\right)=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=2-4x\\\dfrac{4}{3}x+\dfrac{2}{3}-\dfrac{4}{3}x=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2-4x\\\dfrac{2}{3}=1\left(vôlý\right)\end{matrix}\right.\)
=>Hệ phương trình vô nghiệm
b: \(\left\{{}\begin{matrix}x-y\sqrt{2}=0\\2x+y\sqrt{2}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=y\sqrt{2}\\2y\sqrt{2}+y\sqrt{2}=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3y\sqrt{2}=3\\x=y\sqrt{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}\\x=\dfrac{y\sqrt{2}}{2}=\dfrac{\sqrt{2}}{2}\cdot\sqrt{2}=1\end{matrix}\right.\)
c: \(\left\{{}\begin{matrix}5x\sqrt{3}+y=2\sqrt{2}\\x\sqrt{6}-y\sqrt{2}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\sqrt{2}-5x\sqrt{3}\\x\sqrt{6}-\sqrt{2}\left(2\sqrt{2}-5x\sqrt{3}\right)=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\sqrt{6}-4+5x\sqrt{6}=2\\y=2\sqrt{2}-5x\sqrt{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x\sqrt{6}=6\\y=2\sqrt{2}-5\sqrt{3}\cdot x\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{\sqrt{6}}=\dfrac{\sqrt{6}}{6}\\y=2\sqrt{2}-5\sqrt{3}\cdot\dfrac{\sqrt{6}}{6}=-\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)
d: \(\left\{{}\begin{matrix}2\left(x+y\right)+3\left(x-y\right)=4\\\left(x+y\right)+2\left(x-y\right)=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+2y+3x-3y=4\\x+y+2x-2y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x-y=4\\3x-y=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=5x-4\\3x-\left(5x-4\right)=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=5x-4\\-2x+4=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=5\cdot\dfrac{-1}{2}-4=-\dfrac{5}{2}-4=-\dfrac{13}{2}\end{matrix}\right.\)

Trong tam giác ABD, có: \(\dfrac{MA}{MB}=\dfrac{QA}{QD}\) nên MQ//BD và \(\dfrac{QM}{BD}=\dfrac{AM}{AB}\).
CMTT, ta có: NP//BD và \(\dfrac{NP}{BD}=\dfrac{CP}{CD}\)
Nên MQ//NP. Hơn nữa vì \(\dfrac{AM}{AB}=\dfrac{CP}{CD}\) nên \(\dfrac{QM}{BD}=\dfrac{NP}{BD}\Rightarrow QM=NP\)
Do đó tứ giác MNPQ là hình bình hành.
\(\Rightarrow\) MP, NQ cắt nhau tại trung điểm I của mỗi đoạn.
Dựng các hình bình hành AMXE, ABYE, CPZE, CDTE.
Ta có \(\dfrac{MX}{PZ}=\dfrac{AE}{CE}=\dfrac{1}{2}=\dfrac{MI}{IP}\) nên theo định lý Thales thì X, I, Z thẳng hàng và \(\dfrac{IX}{IZ}=\dfrac{IM}{IP}=\dfrac{1}{2}\) hay I là trung điểm XZ
Tương tự như vậy, ta cũng có Y, F, T thẳng hàng và F là trung điểm YT.
Mặt khác, ta có \(\dfrac{EX}{XY}=\dfrac{MA}{MB}=\dfrac{PC}{PD}=\dfrac{ZE}{ZT}\) nên XZ//YT
\(\Rightarrow\dfrac{EZ}{ET}=\dfrac{XZ}{YT}=\dfrac{2IZ}{2FT}=\dfrac{IZ}{FT}\)
Từ đó theo định lý Thales suy ra được E, I, F thẳng hàng (đpcm).

Ta có: \(\tan B=\dfrac{AC}{AB}=\dfrac{3}{4}\)
\(\Rightarrow AC=AB\cdot\dfrac{3}{4}=12\cdot\dfrac{3}{4}=9\) (cm)
Áp dụng định lí Pythagore vào tam giác ABC vuông tại A, ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC^2=12^2+9^2=225\)
\(\Rightarrow BC=\sqrt{225}=15\) (cm) (vì BC>0)
Khi đó: \(\tan B=\dfrac{3}{4}\Rightarrow\widehat{B}\approx37^{\circ}\)

ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{BC^2-AB^2}=5\left(cm\right)\)
Xét ΔABC vuông tại A có
\(sinB=cosC=\dfrac{AC}{BC}=\dfrac{5}{5\sqrt{2}}=\dfrac{1}{\sqrt{2}}\)
\(cosB=sinC=\dfrac{AB}{BC}=\dfrac{5}{5\sqrt{2}}=\dfrac{1}{\sqrt{2}}\)
\(tanB=cotC=\dfrac{AC}{AB}=\dfrac{5}{5}=1\)
\(cotB=tanC=\dfrac{AB}{AC}=\dfrac{5}{5}=1\)
Theo Pytago tam giac ABC vuong tai A
\(AC=\sqrt{BC^2-AB^2}=\sqrt{50-25}=5\)
Do ^B; ^C phu nhau
sinB = AC/BC = 1/can2 = cosC
cosB = AB/BC = 1/can2 = sinC
tanB = AC/AB = 1 = cotC
cotB = AC/AB = 1 = tanC

Lời giải:
$S=\frac{1}{2^0}+\frac{2}{2^1}+\frac{3}{2^2}+....+\frac{2021}{2^{2020}}$
$2S=2+\frac{2}{2^0}+\frac{3}{2^1}+...+\frac{2021}{2^{2019}}$
$\Rightarrow 2S-S=2+\frac{1}{2^0}+\frac{1}{2^1}+...+\frac{1}{2^{2019}}-\frac{2021}{2^{2020}}$
$\Rightarrow S=2+\frac{1}{2^0}+\frac{1}{2^1}+...+\frac{1}{2^{2019}}-\frac{2021}{2^{2020}}$
$2S=4+2+\frac{1}{2^0}+\frac{1}{2^1}+...+\frac{1}{2^{2018}}-\frac{2021}{2^{2019}}$
$\Rightarrow 2S-S=4-\frac{2022}{2^{2019}}$
$\Rightarrow S< 4$


\(x^2-x\left(m+2\right)+2m=0\)
De pt co 2 nghiem phan biet khi delta > 0
\(\Delta=\left(m+2\right)^2-4.2m=m^2+4m+4-8m=m^2-4m+4=\left(m-2\right)^2\)
Ma (m-2)^2 >= 0 voi moi x
=> m - 2 \(\ne0\Rightarrow m\ne2\)
\(x^2-2x-mx+2m=0\)
\(x^2-\left(2+m\right)x+2m=0\)
\(\Delta=\left[-\left(2+m\right)\right]^2-4.1.2m\)
\(=4+4m+m^2-8m\)
\(=m^2-4m+4\)
\(=\left(m-2\right)^2\)
Để phương trình có hai nghiệm phân biệt thì \(\Delta>0\)
\(\left(m-2\right)^2>0\)
\(m-2\ne0\)
\(m\ne2\)
Vậy \(m\ne2\) thì phương trình đã cho có hai nghiệm phân biệt

Giải:
Gọi chiều rộng của mảnh đất hình chữ nhật là: \(x\) (m); \(x\) > 0
Chiều dài của mảnh đất hình chữ nhật là: \(x\) x 2 = 2\(x\) (m)
Chiều dài của cái ao là: 2\(x\) - 1 x 2 = 2\(x\) - 2 (m)
Chiều rộng của cái ao là: \(x\) - 1 x 2 = \(x\) - 2 (m)
Diện tích của cái ao là: (2\(x\) - 2) x (\(x\) - 2)
Theo bài ra ta có phương trình:
(2\(x\) - 2) x (\(x-2\)) = 60
2\(x^2\) - 4\(x\) - 2\(x\) + 4 = 60
2\(x^2\) - (4\(x\) + 2\(x\)) + 4 = 60
2\(x^2\) - 6\(x\) + 4 - 60 = 0
2\(x^2\) - 6\(x\) - 56 = 0
\(\Delta^,\) = 32 - (- 56)x 2 = 121 > 0
Vậy phương trình có hai nghiệm lần lượt là:
\(x_1\) = (3 + \(\sqrt{121}\)) : 2 = 7
\(x_2\) = (3 - \(\sqrt{121}\)): 2 = - 4 < 0 (loại)
Vậy \(x\) = 7
Chiều rộng của mảnh đất là: 7m
Chiều dài của mảnh đất là: 7 x 2 = 14 (m)
Kết luận các kích thước của mảnh đất là chiều rộng 7m; chiều dài 14m
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AB^2+AB^2=10^2\)
=>\(2\cdot AB^2=100\)
=>\(AB^2=50\)
=>\(AB=\sqrt{50}=5\sqrt{2}\left(cm\right)\)