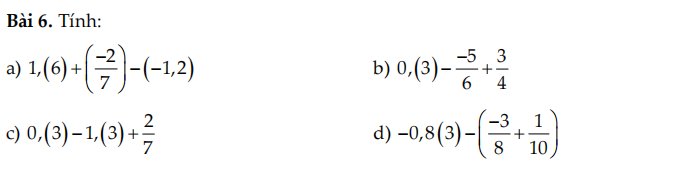
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 7:
a: \(\left[0,\left(30\right)+0,\left(60\right)\right]x=10\)
=>\(\left(\dfrac{10}{33}+\dfrac{20}{33}\right)\cdot x=10\)
=>\(\dfrac{30}{33}\cdot x=10\)
=>\(x\cdot\dfrac{10}{11}=10\)
=>\(x=10:\dfrac{10}{11}=11\)
b: \(0,\left(12\right):1,\left(6\right)=x:0,\left(4\right)\)
=>\(x:\dfrac{4}{9}=\dfrac{4}{33}:\dfrac{5}{3}\)
=>\(x:\dfrac{4}{9}=\dfrac{4}{33}\cdot\dfrac{3}{5}=\dfrac{4}{11\cdot5}=\dfrac{4}{55}\)
=>\(x=\dfrac{4}{55}:\dfrac{4}{9}=\dfrac{9}{55}\)

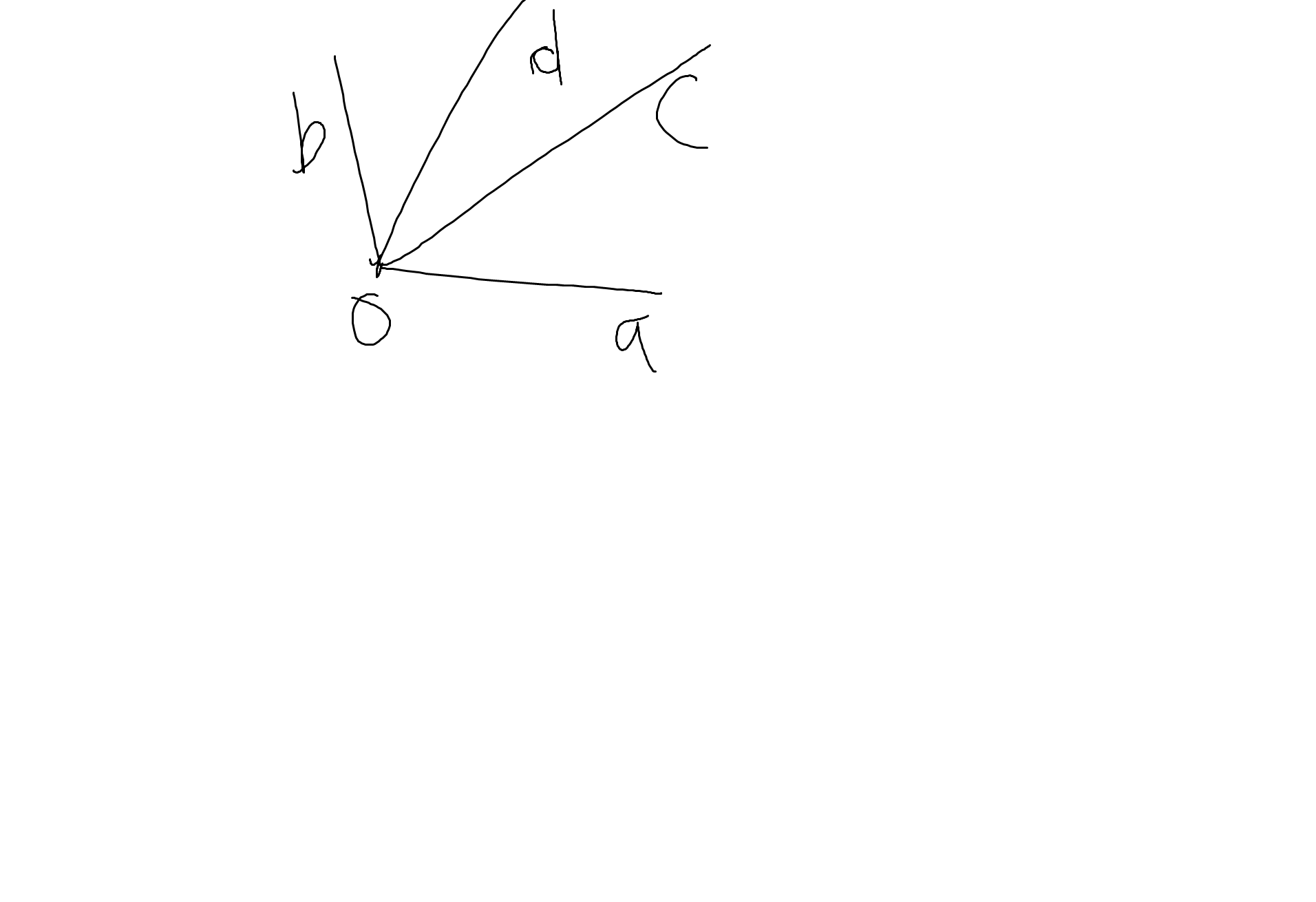
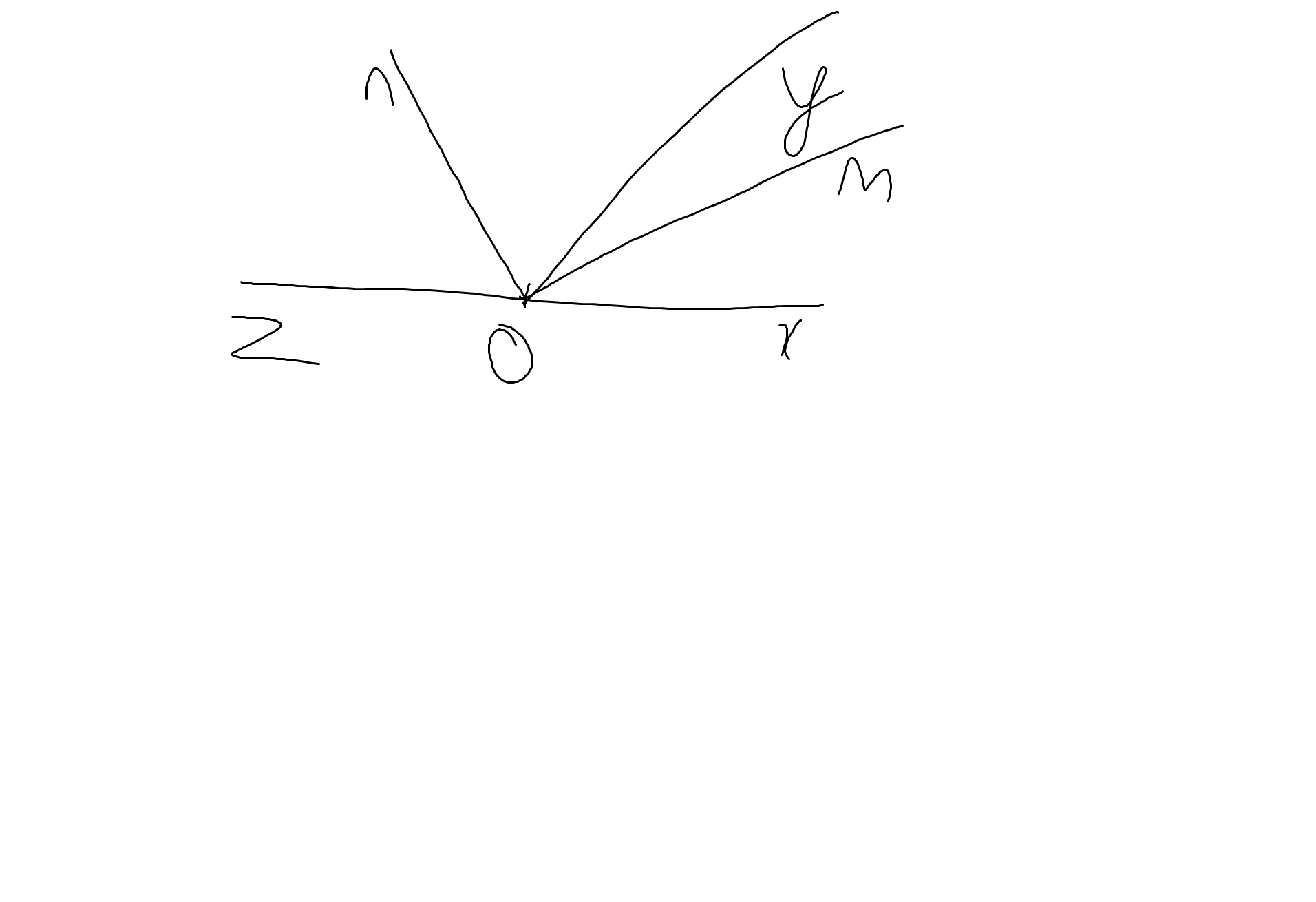
6: \(\widehat{mOn}=\widehat{mOy}+\widehat{nOy}\)
\(=\dfrac{1}{2}\left(\widehat{xOy}+\widehat{zOy}\right)\)
\(=\dfrac{1}{2}\cdot180^0=90^0\)
5:
a: tia Oc nằm giữa hai tia Oa và Ob
=>\(\widehat{aOc}+\widehat{bOc}=\widehat{aOb}\)
=>\(\widehat{bOc}=100^0-40^0=60^0\)
b: Od là phân giác của góc cOb
=>\(\widehat{cOd}=\dfrac{\widehat{cOb}}{2}=\dfrac{60^0}{2}=30^0\)

bài 10:
\(A=1+2012+2012^2+...+2012^{72}\)
=>\(2012A=2012+2012^2+...+2012^{73}\)
=>\(2012A-A=2012+2012^2+...+2012^{73}-1-2012-...-2012^{72}\)
=>\(2011A=2012^{73}-1\)
=>2011A=B
=>B>A
Bài 11:
\(B=\dfrac{3^{10}\cdot11+3^{10}\cdot5}{3^9\cdot2^4}=\dfrac{3^{10}\left(11+5\right)}{3^9\cdot16}=\dfrac{3^{10}}{3^9}=3\)
\(C=\dfrac{2^{10}\cdot13+2^{10}\cdot65}{2^8\cdot104}=\dfrac{2^{10}\left(13+65\right)}{2^8\cdot104}=\dfrac{2^2\cdot78}{104}=\dfrac{4\cdot2}{3}=\dfrac{8}{3}\)
mà \(3>\dfrac{8}{3}\)
nên B>C


Bài 2:
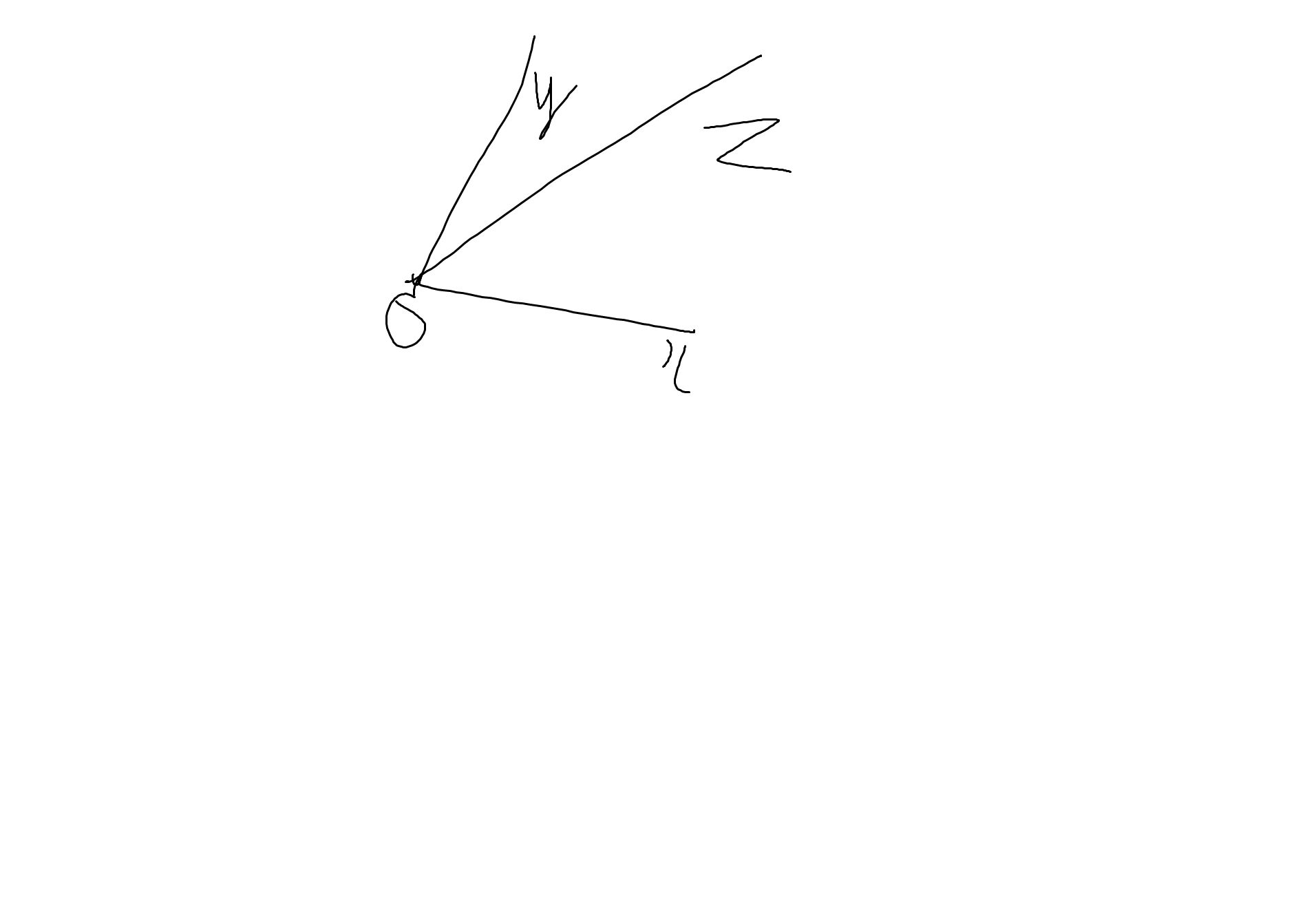
Vì \(\widehat{xOz}< \widehat{xOy}\left(50^0< 80^0\right)\)
nên tia Oz nằm giữa hai tia Ox,Oy
=>\(\widehat{xOz}+\widehat{yOz}=\widehat{xOy}\)
=>\(\widehat{yOz}=80^0-50^0=30^0\)
Bài 4:
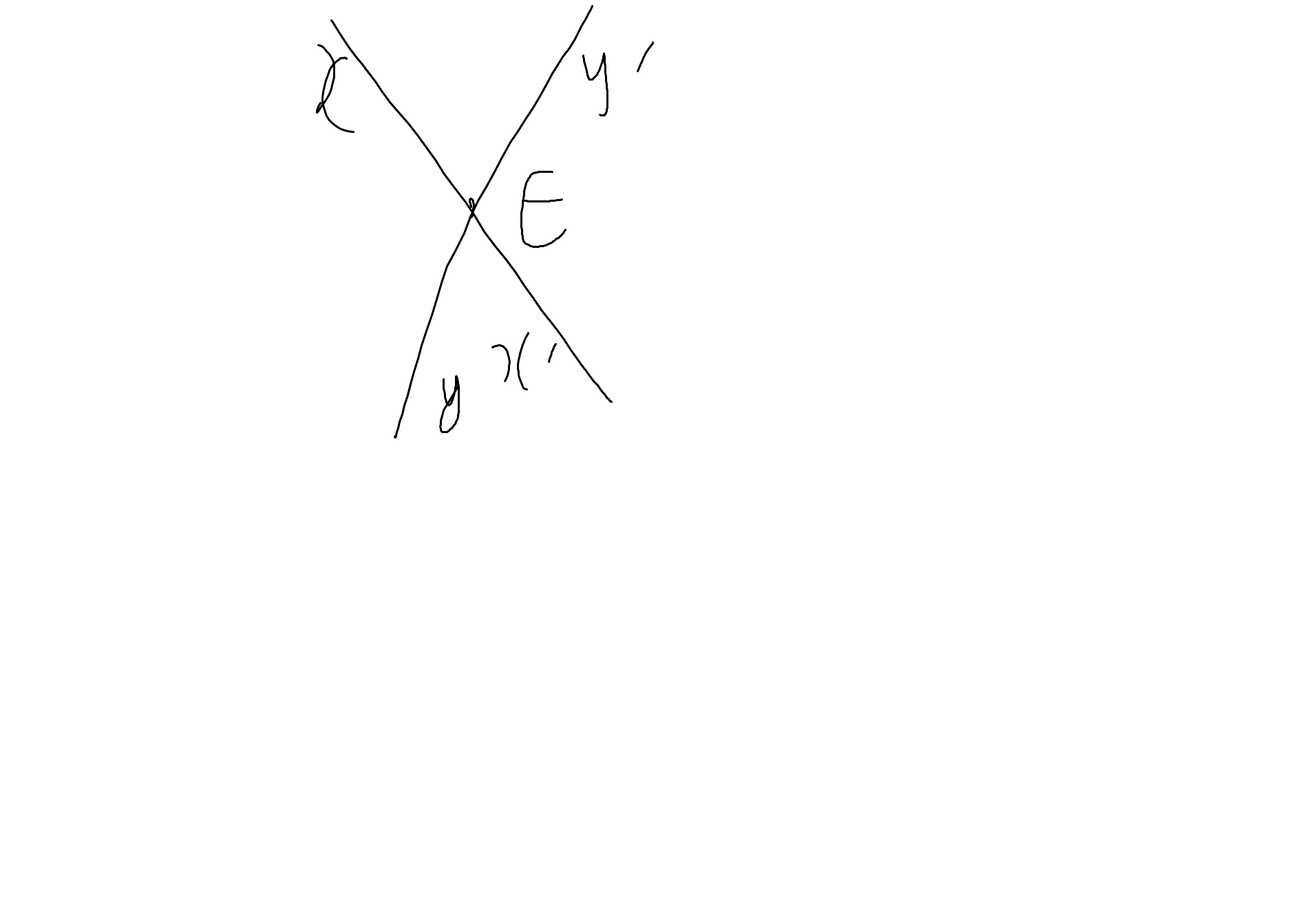
Ta có: \(\widehat{xEy}+\widehat{xEy'}=180^0\)(hai góc kề bù)
=>\(\widehat{xEy'}=180^0-50^0=130^0\)
Ta có: \(\widehat{xEy}=\widehat{x'Ey'}\)(hai góc đối đỉnh)
mà \(\widehat{xEy}=50^0\)
nên \(\widehat{x'Ey'}=50^0\)
Ta có: \(\widehat{xEy'}=\widehat{x'Ey}\)(hai góc đối đỉnh)
mà \(\widehat{xEy'}=130^0\)
nên \(\widehat{x'Ey}=130^0\)

kẻ CM//a và DN//bB(CM và Aa nằm cùng phía với nửa mặt phẳng chứa tia AC, DN và Bb nằm khác phía với nửa mặt phẳng chứa tia DB
CM//Aa
=>\(\widehat{MCA}=\widehat{A_1}\)
Ta có: CM//a
DN//b
mà a//b
nên CM//DN//a//b
CM//DN
=>\(\widehat{MCD}=\widehat{CDN}\)
DN//Bb
=>\(\widehat{NDB}=\widehat{B_1}\)
Ta có: \(\widehat{ACD}=\widehat{ACM}+\widehat{CDM}=\widehat{CDN}+\widehat{B_1}\)
\(\widehat{CDB}=\widehat{CDN}+\widehat{NDB}=\widehat{CDN}+\widehat{B_1}\)
Do đó: \(\widehat{ACD}=\widehat{CDB}\)

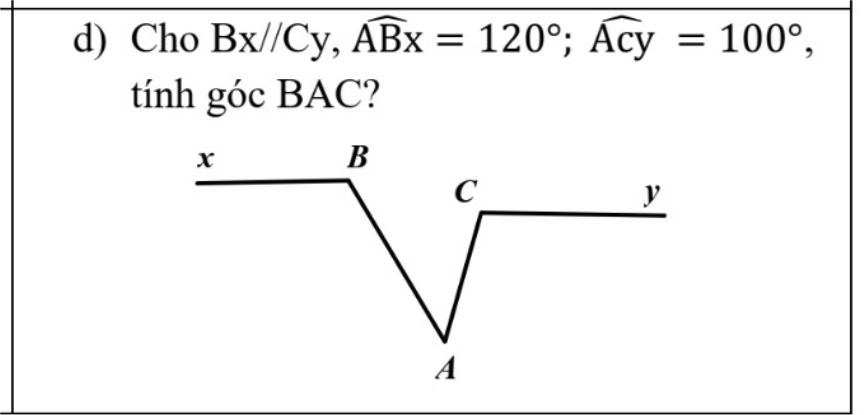
Gọi F là giao điểm của Cy với AB
Bx//Cy
=>\(\widehat{BFC}=\widehat{xBC}\)(hai góc so le trong)
=>\(\widehat{BFC}=120^0\)
Ta có: \(\widehat{BFC}+\widehat{AFC}=180^0\)(hai góc kề bù)
=>\(\widehat{AFC}+120^0=180^0\)
=>\(\widehat{AFC}=60^0\)
Ta có: \(\widehat{ACF}+\widehat{ACy}=180^0\)(hai góc kề bù)
=>\(\widehat{ACF}+100^0=180^0\)
=>\(\widehat{ACF}=80^0\)
Xét ΔACF có \(\widehat{AFC}+\widehat{ACF}+\widehat{CAF}=180^0\)
=>\(\widehat{BAC}=180^0-60^0-80^0=40^0\)

Bài 5
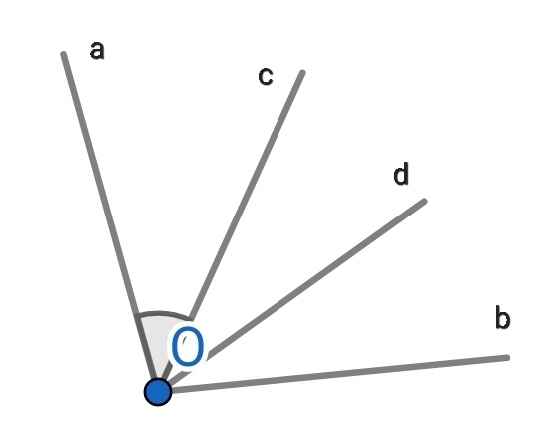
a) Do Oc nằm giữa hai tia Oa và Ob nên
∠aOc + ∠cOb = ∠aOb
⇒ ∠cOb = ∠aOb - ∠aOc
= 100⁰ - 40⁰
= 60⁰
b) Do Od là tia phân giác của ∠cOb (gt)
⇒ ∠cOd = ∠cOb : 2
= 60⁰ : 2
= 30⁰

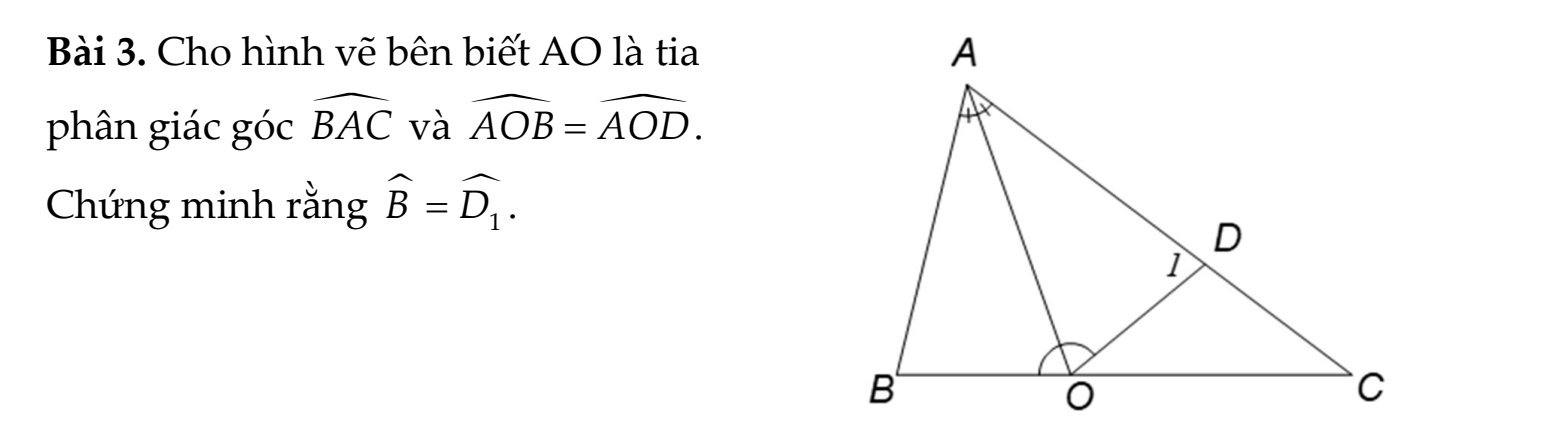
Xét 2 ΔABO và ΔADO ta có:
\(\widehat{BAO}=\widehat{DAO}\) (AD là phân giác của góc BAC)
\(OA\) chung
\(\widehat{AOB}=\widehat{AOD}\left(gt\right)\)
\(=>\Delta ABO=\Delta ADO\left(g.c.g\right)\)
\(=>\widehat{B}=\widehat{D_1}\) (hai góc tương ứng)


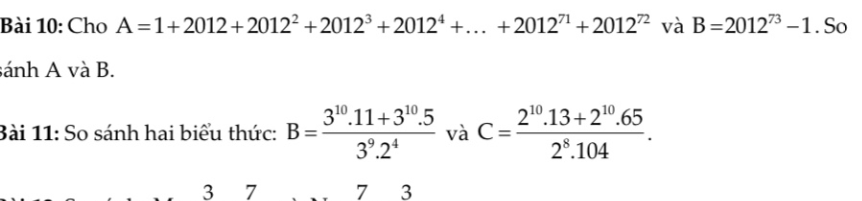
 mn lm giup e vs
mn lm giup e vs 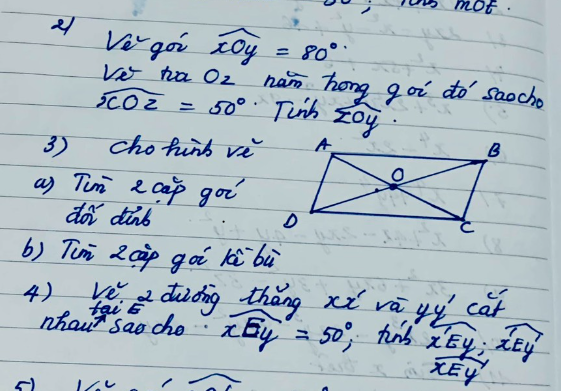 vẽ hình luôn dk ạ mih cần đoạn vẻ hình
vẽ hình luôn dk ạ mih cần đoạn vẻ hình

a: \(1,\left(6\right)+\left(\dfrac{-2}{7}\right)-\left(-1,2\right)\)
\(=\dfrac{5}{3}-\dfrac{2}{7}+\dfrac{6}{5}\)
\(=\dfrac{175}{105}-\dfrac{30}{105}+\dfrac{126}{105}=\dfrac{271}{105}\)
b: \(0,\left(3\right)-\dfrac{-5}{6}+\dfrac{3}{4}=\dfrac{1}{3}+\dfrac{5}{6}+\dfrac{3}{4}\)
\(=\dfrac{4}{12}+\dfrac{10}{12}+\dfrac{9}{12}=\dfrac{23}{12}\)
c: \(0,\left(3\right)-1,\left(3\right)+\dfrac{2}{7}=\dfrac{1}{3}-\dfrac{4}{3}+\dfrac{2}{7}=-1+\dfrac{2}{7}=-\dfrac{5}{7}\)
d: \(-0,8\left(3\right)-\left(\dfrac{-3}{8}+\dfrac{1}{10}\right)\)
\(=-\dfrac{5}{6}+\dfrac{3}{8}-\dfrac{1}{10}\)
\(=-\dfrac{100}{120}+\dfrac{45}{120}-\dfrac{12}{120}=\dfrac{-67}{120}\)