Một thửa ruộng hình chữ nhật có chiều dài 320 m, chiều rộng bằng 3/8 chiều dài. Trung bình cứ 100 m2 thửa ruộng đó thu hoạch được 70 kg thóc. Hỏi trên cả thửa ruộng đó người ta thu hoạch được bao nhiêu ki-lô-gam thóc?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bài giải
Tổng của chiều dài và chiều rộng là:
960 : 2 = 480 (m)
Tổng số phần bằng nhau là:
2 + 1 = 3 ( phần )
Chiều rộng trên bản đồ là:
(480 : 3) x 1 = 160 (m)
Chiều dài trên bản đồ là:
(480 : 3) x 2 = 320 (m)
Diện tích của mảnh đất là:
320 x 160= 51200 (m2)
Diện tích của mảnh đất trên bản đồ tỉ lệ 1:1000 là:
51200 : 1000 = 52,1 (m2)
đ/s:.....
Chiều dài gấp 2 lần chiều rộng suy ra chiều rộng bằng 1/2 chiều dài
Nửa chu vi là :
960:2=480(m)
Chiều dài thực tế là :
480:(2+1)x2=320(m)
Chiều rộng thực tế là :
480-320=160(m)
Chiều dài trên bản đồ là :
320:1000=0,32(m)
Chiều rộng trên bản đồ là :
0,32x1/2=0,16
Diện tích mảnh đất trên bản đồ là :
0,32x0,16=0,0512(m2)
Đáp sô : ...
Chúc hok tốt

1: BC=BH+CH=4+9=13(cm)
Xét ΔHAB vuông tại H và ΔACB vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔHAB~ΔACB
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)
=>\(BA^2=BH\cdot BC=4\cdot13=52\)
=>\(BA=\sqrt{52}=2\sqrt{13}\left(cm\right)\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=13^2-\left(2\sqrt{13}\right)^2=117\)
=>\(AC=\sqrt{117}=3\sqrt{13}\left(cm\right)\)
2: ΔHAB~ΔACB
=>\(\dfrac{HA}{AC}=\dfrac{AB}{CB}\)
=>\(HA=\dfrac{AB\cdot AC}{BC}=\dfrac{2\sqrt{13}\cdot3\sqrt{13}}{13}=6\left(cm\right)\)
Xét tứ giác AKHE có \(\widehat{AKH}=\widehat{AEH}=\widehat{KAE}=90^0\)
nên AKHE là hình chữ nhật
=>AH=KE
=>KE=6(cm)
3: Xét ΔAKH vuông tại K và ΔAHB vuông tại H có
\(\widehat{HAB}\) chung
Do đó: ΔAKH~ΔAHB
=>\(\dfrac{AK}{AH}=\dfrac{AH}{AB}\)
=>\(AH^2=AK\cdot AB\left(1\right)\)
Xét ΔAEH vuông tại E và ΔAHC vuông tại H có
\(\widehat{EAH}\) chung
Do đó: ΔAEH~ΔAHC
=>\(\dfrac{AE}{AH}=\dfrac{AH}{AC}\)
=>\(AH^2=AE\cdot AC\left(2\right)\)
Từ (1),(2) suy ra \(AK\cdot AB=AE\cdot AC\)
=>\(\dfrac{AK}{AC}=\dfrac{AE}{AB}\)
Xét ΔAKE vuông tại A và ΔACB vuông tại A có
\(\dfrac{AK}{AC}=\dfrac{AE}{AB}\)
Do đó: ΔAKE~ΔACB
4: ta có: ΔABC vuông tại A
mà AI là đường trung tuyến
nên IA=IC
=>ΔIAC cân tại I
=>\(\widehat{IAC}=\widehat{ICA}\)
ΔAKE~ΔACB
=>\(\widehat{AEK}=\widehat{ABC}\)
Ta có: \(\widehat{AEK}+\widehat{IAC}=\widehat{ABC}+\widehat{ACB}=90^0\)
=>EK\(\perp\)AI tại N
1. Tính AB, AC:
- Áp dụng định lý Pitago trong tam giác vuông AHB:
- AB² = AH² + HB²
- AH² = AB² - HB²
- Áp dụng định lý Pitago trong tam giác vuông AHC:
- AC² = AH² + HC²
- AH² = AC² - HC²
- Từ hai phương trình trên, ta có: AB² - HB² = AC² - HC²
- Suy ra: AB² = AC² - HC² + HB²
- Thay số: AB² = AC² - 9² + 4² = AC² - 65
- Áp dụng định lý Pitago trong tam giác vuông ABC:
- BC² = AB² + AC²
- BC² = (AC² - 65) + AC² = 2AC² - 65
- Thay BC = HB + HC = 4 + 9 = 13
- 13² = 2AC² - 65
- 2AC² = 13² + 65 = 224
- AC² = 112
- AC = √112 = 4√7 cm
- Thay AC vào phương trình AB² = AC² - 65:
- AB² = (4√7)² - 65 = 112 - 65 = 47
- AB = √47 cm
2. Tính KE:
- Áp dụng định lý Pitago trong tam giác vuông AKE:
- KE² = AK² + AE²
- Áp dụng định lý Pitago trong tam giác vuông AHB:
- AK² = AH² - HK²
- Áp dụng định lý Pitago trong tam giác vuông AHC:
- AE² = AH² - HE²
- Thay vào phương trình KE²:
- KE² = (AH² - HK²) + (AH² - HE²) = 2AH² - (HK² + HE²)
- Ta có: HK + HE = BC = 13 cm
- Áp dụng định lý Pitago trong tam giác vuông HKE:
- KE² = HK² + HE² = (HK + HE)² - 2HK.HE = 13² - 2HK.HE
- Suy ra: 2AH² - (HK² + HE²) = 13² - 2HK.HE
- 2AH² = 13² + 2HK.HE
- AH² = (13² + 2HK.HE) / 2
- Thay AH² = AB² - HB²:
- AB² - HB² = (13² + 2HK.HE) / 2
- 2(AB² - HB²) = 13² + 2HK.HE
- 2HK.HE = 2(AB² - HB²) - 13²
- HK.HE = (AB² - HB²) - 13²/2
- HK.HE = (47 - 4²) - 13²/2 = -65/2
- Vì HK và HE đều dương nên HK.HE = -65/2 là vô lý.
- Vậy, không thể tính KE bằng cách này.
3. Chứng minh AB.AK = AE.AC; AKE ~ ACB:
- Chứng minh AB.AK = AE.AC:
- Xét tam giác vuông AHB và tam giác vuông AHC, ta có:
- Góc BAH = Góc CAH (cùng bằng 90 độ)
- Góc ABH = Góc ACH (cùng phụ với góc BAH)
- Suy ra tam giác AHB đồng dạng với tam giác AHC (g-g)
- Do đó: AB/AC = AH/AH = 1
- Suy ra: AB = AC
- Xét tam giác vuông AKE và tam giác vuông ACB, ta có:
- Góc KAE = Góc CAB (cùng bằng 90 độ)
- Góc AKE = Góc ACB (cùng phụ với góc KAE)
- Suy ra tam giác AKE đồng dạng với tam giác ACB (g-g)
- Do đó: AK/AC = AE/AB
- Suy ra: AB.AK = AE.AC
- Xét tam giác vuông AHB và tam giác vuông AHC, ta có:
- Chứng minh AKE ~ ACB:
- Xét tam giác vuông AKE và tam giác vuông ACB, ta có:
- Góc KAE = Góc CAB (cùng bằng 90 độ)
- Góc AKE = Góc ACB (cùng phụ với góc KAE)
- Suy ra tam giác AKE đồng dạng với tam giác ACB (g-g)
- Xét tam giác vuông AKE và tam giác vuông ACB, ta có:
4. Chứng minh AI vuông góc KE tại N:
- Xét tam giác ABC:
- I là trung điểm của BC nên AI là đường trung tuyến của tam giác ABC.
- Xét tam giác AKE:
- N là giao điểm của AI và KE nên N là trọng tâm của tam giác AKE.
- Theo tính chất trọng tâm của tam giác:
- Trọng tâm của tam giác cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó.
- Do đó: AN = 2/3 AI
- Xét tam giác vuông AHI:
- AI là đường trung tuyến của tam giác vuông AHI nên AI = 1/2 HI.
- Suy ra:
- AN = 2/3 AI = 2/3 * (1/2 HI) = 1/3 HI
- Do đó: IN = AI - AN = 1/2 HI - 1/3 HI = 1/6 HI
- Xét tam giác vuông HKE:
- N là trung điểm của KE nên HN là đường trung tuyến của tam giác vuông HKE.
- Theo tính chất đường trung tuyến của tam giác vuông:
- Đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
- Do đó: HN = 1/2 KE
- Suy ra:
- IN = 1/6 HI = 1/2 HN
- Do đó: HN = 3IN
- Xét tam giác HIN:
- HN = 3IN nên tam giác HIN vuông tại I (định lý đảo của định lý Pytago).
- Kết luận:
- AI vuông góc KE tại N.
Lưu ý:
- Trong bài toán này, không thể tính KE bằng cách sử dụng định lý Pitago trong tam giác vuông HKE vì HK.HE là một số âm.
- Việc chứng minh AB.AK = AE.AC và AKE ~ ACB là cần thiết để chứng minh AI vuông góc KE tại N.
- Việc chứng minh AI vuông góc KE tại N là một ứng dụng của tính chất trọng tâm của tam giác và tính chất đường trung tuyến của tam giác vuông.


Đề thiếu dữ liệu về độ dài quãng đường AB hoặc vận tốc hai xe rồi em!
Cj ơi, em vẫn thấy ở dưới có câu trả lời của anh Akai Hamura ý ạ , e mún hỏi có cách làm nào khác thôi cảm ơn cj

a: Xét tứ giác ABMD có
AD//BM
AB//MD
Do đó: ABMD là hình bình hành
=>AD=BM; AB=MD
Xét tứ giác AEMC có
AE//MC
AC//ME
Do đó: AEMC là hình bình hành
=>AE=MC; ME=AC
Ta có: AE+AD=DE
BM+MC=BC
mà AD=BM và MC=AE
nên DE=BC
Xét ΔABC và ΔMDE có
AB=MD
BC\DE
AC=ME
Do đó: ΔABC=ΔMDE
b: Ta có: AEMC là hình bình hành
=>AM cắt EC tại trung điểm của mỗi đường(1)
Ta có: ABMD là hình bình hành
=>AM cắt BD tại trung điểm của mỗi đường(2)
Từ (1),(2) suy ra AM,EC,BD đồng quy



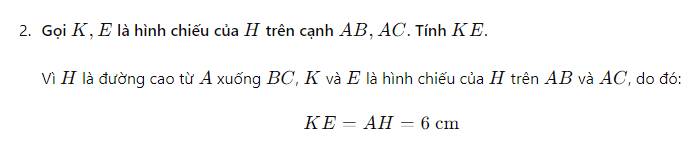

Giải:
Chiều rộng của thửa ruộng hình chữ nhật đó là:
320 x \(\dfrac{3}{8}\) = 120 ( m )
Diện tích thửa ruộng hình chữ nhật đó là:
320 x 120 = 38400 ( m2 )
Trên cả thửa ruộng đó người ta thu hoạch được số ki-lô-gam thóc là:
70 x ( 38400 : 100 ) = 26880 ( kg )
Đáp số: 26880 kg thóc
Chiều rộng thửa ruộng đó là :
320x3/8=120(m)
Diện tích thửa ruộng đó là :
320x120=38400(m2)
Trên cả thửa ruộng đó người ta thu hoạch được số ki-lô-gam thóc là:
38400:100x70=26880(kg)
Đáp số : 26880 ki-lô-gam.