K
Khách
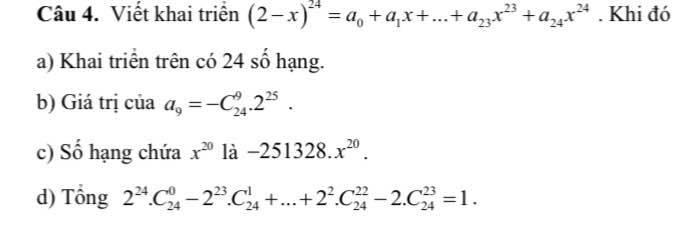
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
11 tháng 5 2024
Gọi các số thỏa mãn ycbt là \(\overline{\alpha\beta\gamma\delta}\)
Khi đó \(\delta\in\left\{4,6,8\right\}\) -> Có 3 cách.
TH1: \(\alpha,\beta,\gamma\) đều lẻ \(\Rightarrow\) Có \(A^3_4=24\) cách.
TH2: Trong các số \(\alpha,\beta,\gamma\) có đúng 1 số chẵn
\(\Rightarrow\) Có \(3.2.4.3=72\) cách.
TH3: Trong các số \(\alpha,\beta,\gamma\) có đúng 1 số lẻ.
\(\Rightarrow\) Có \(3.4.2.1=24\) cách.
\(\Rightarrow\) Có tất cả \(24+72+24=120\) cách chọn bộ \(\left(\alpha,\beta,\gamma\right)\)
\(\Rightarrow\) Có tất cả \(3.120=360\) số thỏa mãn ycbt.
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 5 2024
Câu a là lấy mấy viên để xác suất có 3 viên đỏ em? Đề bài thiếu.
b.
Không gian mẫu: \(C_{20}^4\)
Số cách lấy 2 viên đỏ, 2 viên xanh: \(C_{12}^2.C_8^2\)
Xác suất: \(P=\dfrac{C_{12}^2.C_8^2}{C_{20}^2}=\)
10 tháng 5 2024
Câu 1: D
Câu 2: C
Câu 3: Thay x=1 và y=2 vào y=4x+m-1, ta được:
\(m-1+4\cdot1=2\)
=>m+3=2
=>m=-1
=>Chọn B
Câu 4: B
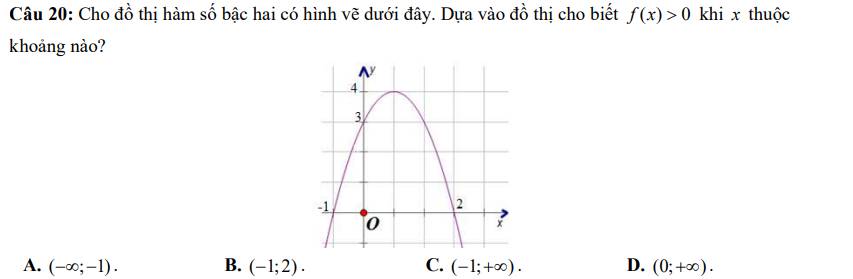
Câu 5: Hoành độ đỉnh là:
\(x=-\dfrac{b}{2a}=\dfrac{-\left(-6\right)}{2\cdot\left(-2\right)}=\dfrac{6}{-4}=-\dfrac{3}{2}\)
=>Chọn C
Câu 6:
Phương trình hoành độ giao điểm là:
\(x^2-4x=-x-2\)
=>\(x^2-3x+2=0\)
=>(x-1)(x-2)=0
=>\(\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Thay x=1 vào y=-x-2, ta được:
y=-1-2=-3
Thay x=2 vào y=-x-2, ta được:
y=-2-2=-4
=>Chọn D
Câu 7: A
Câu 8: \(f\left(x\right)=-2x^2+8x-8\)
\(=-2\left(x^2-4x+4\right)\)
\(=-2\left(x-2\right)^2< =0\forall x\)
=>Chọn C
Câu 9: \(x^4-5x^2+4< 0\)
=>\(\left(x^2-1\right)\left(x^2-4\right)< 0\)
=>\(1< x^2< 4\)
=>\(\left[{}\begin{matrix}1< x< 2\\-2< x< -1\end{matrix}\right.\)
=>Chọn D
Câu 10:
ĐKXĐ: \(x\in R\)
\(x^2-x+2=2x^2-4x+4\)
=>\(-x^2+3x-2=0\)
=>\(x^2-3x+2=0\)
=>(x-1)(x-2)=0
=>\(\left[{}\begin{matrix}x=1\left(nhận\right)\\x=2\left(nhận\right)\end{matrix}\right.\)
=>Chọn B
TN
Trần Nguyễn Phương Thảo
CTVHS
VIP
10 tháng 5 2024
Thi không giúp được bạn nhé!
Mà có giúp cũng đâu có bài đâu mà giúp ^^
9 tháng 5 2024
\(\left(2-x\right)^{24}=\left(x-2\right)^{24}=\sum\limits^{24}_{k=0}C^k_{24}.x^k.\left(-2\right)^{24-k}\)
b) Hệ số tổng quát là \(a_k=C^k_{24}\left(-2\right)^{24-k}\) \(\Rightarrow a_9=C^9_{24}.\left(-2\right)^{24-9}=-2^{15}.C^9_{24}\) -> Sai
c) SHTQ: \(T_k=C^k_{24}.x^k.\left(-2\right)^{24-k}\)
\(x^{20}\Rightarrow k=20\) \(\Rightarrow T_4=C^{20}_{24}.x^{20}\left(-2\right)^{24-20}=170016x^{20}\) -> Sai
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 5 2024
SHTQ trong khai triển \(\left(2-x\right)^{24}\) là: \(C_{24}^k.\left(-x\right)^k.2^{24-k}=C_{24}^k.\left(-1\right)^k.2^{24-k}.x^k\)
b.
Số hạng chứa \(x^9\Rightarrow k=9\)
\(\Rightarrow a_9=C_{24}^9.\left(-1\right)^9.2^{24-9}=-C_{24}^9.2^{15}\)
c.
Số hạng chứa \(x^{20}\Rightarrow k=20\)
Số hạng đó là:
\(C_{24}^{20}.\left(-1\right)^{20}.2^{24-20}.x^{20}=C_{24}^{20}.2^4.x^{20}=170016.x^{20}\)