Phương trình hoành độ giao điểm là:

\(\dfrac{1}{2}x^2=mx-2m+2\)

=>\(\dfrac{1}{2}x^2-mx+2m-2=0\)

\(\text{Δ}=\left(-m\right)^2-4\cdot\dfrac{1}{2}\left(2m-2\right)\)

\(=m^2-2\left(2m-2\right)=m^2-4m+4=\left(m-2\right)^2>=0\forall m\)

Để (d) cắt (P) tại hai điểm phân biệt thì Δ>0

=>\(\left(m-2\right)^2>0\)

=>\(m-2\ne0\)

=>\(m\ne2\)

Theo Vi-et, ta có:

\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m\\x_1x_2=\dfrac{c}{a}=\left(2m-2\right):\dfrac{1}{2}=4m-4\end{matrix}\right.\)

\(\left\{{}\begin{matrix}x_2=8x_1\\x_1+x_2=2m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x_1=2m\\x_2=8x_1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x_1=\dfrac{2}{9}m\\x_2=8\cdot\dfrac{2}{9}m=\dfrac{16}{9}m\end{matrix}\right.\)

\(x_1x_2=4m-4\)

=>\(\dfrac{2}{9}m\cdot\dfrac{16}{9}m=4m-4\)

=>\(\dfrac{32}{81}m^2-4m+4=0\)(1)

\(\text{Δ}=\left(-4\right)^2-4\cdot\dfrac{32}{81}\cdot4=\dfrac{784}{81}\)

Do đó: phương trình (1) có hai nghiệm phân biệt là:

\(\left\{{}\begin{matrix}m_1=\dfrac{4-\dfrac{28}{9}}{2\cdot\dfrac{32}{81}}=\dfrac{9}{8}\left(nhận\right)\\m_2=\dfrac{4+\dfrac{28}{9}}{2\cdot\dfrac{32}{81}}=9\left(nhận\right)\end{matrix}\right.\)

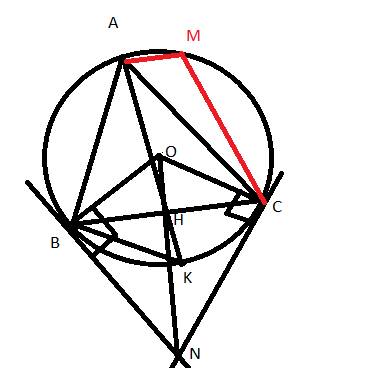
a) Ta có ∠MAB + ∠MOB = 90° + 90° = 180° (vì MA, MB là tiếp tuyến của (O) tại A, B)
Suy ra, tứ giác MAOB nội tiếp.

- SC.SB = SA.SE:

Ta có ∠SCE = ∠SAE = 90° (vì EC là đường kính của (O))
Suy ra, tam giác SCE và tam giác SAE vuông cùng tại E và có cạnh chung là SE
Do đó, SC.SB = SA.SE theo định lý hình chiếu.

b) Ta có ∠ACS = ∠AOM = 90° và ∠CAS = ∠MAO (vì tứ giác MAOB nội tiếp)
Suy ra, tam giác ACS đồng dạng tam giác AOM theo định lý đồng dạng tam giác góc-góc.
Ta có ∠MAS = ∠ACS = 90° và ∠AMO = ∠CAO (vì tứ giác MAOB nội tiếp)
Suy ra, tam giác MAS đồng dạng tam giác AOC theo định lý đồng dạng tam giác góc-góc.
Vì vậy, tam giác MAS cân tại A.

c) Ta có ∠CBA = ∠COA (vì tứ giác MAOB nội tiếp)
Và ∠COA = ∠DOE (vì EC là đường kính của (O))
Và ∠DOE = ∠NDE (vì DE // ON)
Suy ra, ∠CBA = ∠NDE.

a: Xét (O) có

ΔBAC nội tiếp

BC là đường kính

Do đó; ΔBAC vuông tại A

=>BA\(\perp\)AC

mà BA//OK

nên OK\(\perp\)AC 

Ta có: ΔOAC cân tại O

mà OK là đường cao

nên OK là phân giác của góc AOC

Xét ΔOCI và ΔOAI có

OC=OA

\(\widehat{COI}=\widehat{AOI}\)

OI chung

Do đó: ΔOCI=ΔOAI

=>\(\widehat{OAI}=\widehat{OCI}=90^0\)

=>IA là tiếp tuyến của (O)

b: Ta có: \(\widehat{ICK}+\widehat{OCK}=90^0\)

\(\widehat{ACK}+\widehat{OKC}=90^0\)(KO\(\perp\)AC)

mà \(\widehat{OCK}=\widehat{OKC}\)(OK=OC)

nên \(\widehat{ICK}=\widehat{ACK}\)

=>CK là phân giác của góc ACI

Lời giải:

a. Xét tứ giác $AHBC$ có $\widehat{BHC}=\widehat{BAC}=90^0$ và cùng nhìn cạnh $BC$ nên $AHBC$ là tứ giác nội tiếp.

b.

Do $AHBC$ là tứ giác nội tiếp nên:

$\widehat{EHA}=\widehat{ACB}=45^0$ (do $ABC$ là tam giác vuông cân tại $A$)

c.

Xét tam giác $EAH$ và $EBC$ có:

$\widehat{E}$ chung

$\widehat{EHA}=\widehat{ACB}=\widehat{ECB}$ (cmt)

$\Rightarrow \triangle EAH\sim \triangle EBC$ (g.g)

d.

Xét tứ giác $ADHE$ có tổng hai góc đối $\widehat{EHD}+\widehat{DAE}=90^0+90^0=180^0$

$\Rightarrow ADHE$ là tứ giác nội tiếp

$\Rightarrow \widehat{EDA}=\widehat{EHA}=45^0$

Tam giác $EDA$ có $\widehat{A}=90^0$ và $\widehat{D}=45^0$ nên $EDA$ là tam giác vuông cân tại $A$

$\Rightarrow AD=AE$

a. Ta có ∠HAB = ∠HCB (cùng chắn cung HB) và ∠HBA = ∠HCA (cùng chắn cung HA). Do đó, tứ giác AHBC nội tiếp.

b. Góc AHE = 90° - ∠AEB = 90° - ∠ACB = ∠ABC = 45° (vì tam giác ABC vuông cân tại A).

c. Ta có ∠EHA = ∠EBC (cùng chắn cung EB) và ∠EAH = ∠EBA = ∠EBC (vì tam giác ABC vuông cân tại A). Do đó, tam giác EAH và EBC đồng dạng.

d. Vì tam giác EAH và EBC đồng dạng nên EA/EB = AH/BC. Nhưng AH = BC (vì tam giác ABC vuông cân tại A) nên EA = EB. Mà AB = AE + EB = 2EA. Do đó, AD = AB/2 = EA = AE.

a: Gọi O là trung điểm của AC

=>O là tâm đường tròn đường kính AC

Xét (O) có

ΔABC nội tiếp

AC là đường kính

Do đó: ΔABC vuông tại B

=>BC\(\perp\)AB tại B

Xét (O) có

ΔADC nội tiếp

AC là đường kính

Do đó: ΔADC vuông tại D

=>AD\(\perp\)DC tại D

Xét ΔAEF có

FB,ED là các đường cao

FB cắt ED tại C

Do đó: C là trực tâm của ΔAEF

=>AC\(\perp\)EF

b: Xét ΔDFC vuông tại D và ΔDEA vuông tại D có

\(\widehat{DFC}=\widehat{DEA}\left(=90^0-\widehat{BAD}\right)\)

Do đó;ΔDFC~ΔDEA

=>\(\dfrac{DF}{DE}=\dfrac{DC}{DA}\)

=>\(DF\cdot DA=DC\cdot DE\)

c: Xét tứ giác BDFE có \(\widehat{EDF}=\widehat{EBF}=90^0\)

nên BDFE là tứ giác nội tiếp

Tứ giác ABCD nội tiếp đường tròn với đường kính AC có các tính chất sau:

a. EF vuông góc với AC: Điều này có thể được suy ra từ tính chất của tứ giác nội tiếp, trong đó tổng số đo hai góc đối diện bằng 180°.

b. DA . DF = DC . DE: Đây là một tính chất của tứ giác nội tiếp, nơi tích của độ dài hai cạnh không liên tiếp bằng nhau.

c. Tứ giác BDFE nội tiếp: Điều này có thể được chứng minh bằng cách sử dụng các tính chất của tứ giác nội tiếp, trong đó tổng số đo hai góc đối diện bằng 180°

Bài 9:

Phương trình hoành độ giao điểm là:

\(3x^2=2x-m\)

=>\(3x^2-2x+m=0\)

Để (P) cắt (d) tại hai điểm phân biệt nằm về hai phía của trục tung thì a*c<0

=>3m<0

=>m<0

Bài 8:
Phương trình hoành độ giao điểm là:

\(-2x^2=x+m-1\)

=>\(2x^2+x+m-1=0\)

Để (P) cắt (d) tại hai điểm phân biệt thì a*c<0

=>2(m-1)<0

=>m-1<0

=>m<1