Bước đầu tiên, chúng ta hãy xem xét phần (b+1)(b+2)(b + 1)(b + 2):

Do đó, phương trình trở thành:

Bây giờ, ta thử từng giá trị của aa để tìm bb:

1. Thử a=8a = 8 (vì 28=2562^8 = 256)

Giải phương trình bậc hai:

Giải phương trình bậc hai này bằng công thức nghiệm:

Áp dụng cho a=1,b=3,c=−1183a = 1, b = 3, c = -1183:

Bởi vì căn bậc hai của 4736 không phải là số nguyên, giá trị bb sẽ không phải là số tự nhiên.

1. Thử a=9a = 9 (vì 29=5122^9 = 512)

Giải phương trình bậc hai:

Giải phương trình bậc hai này bằng công thức nghiệm:

Bởi vì căn bậc hai của 5756 không phải là số nguyên, giá trị bb sẽ không phải là số tự nhiên.

Tiếp tục thử các giá trị khác của aa hoặc kiểm tra lại giả thiết và bài toán để tìm ra lời giải chính xác hơn (nếu bạn thấy tôi đúng)

  12,56 x 10 + 26,43 : 0,1 + 10

= 12,56  x 10 + 26,43 x 10 + 10 x 1

= 10 x (12,56 + 26,43 + 1)

= 10 x (38,99 + 1)

= 10 x 39,99

= 399,9 

XẾP THÀNH 3 ,4,9 HÀNG NGHĨA LÀ SỐ HỌC SINH LỚP ĐÓ LÀ SỐ CHIA HẾT CHO 3,4,9

SUY RA : SỐ HỌC SINH LỚP ĐÓ LÀ 36

                      Giải:

Vì số học sinh lớp 6A xếp hàng 3, hàng 4 hàng 9 đều vừa đủ nên số học sinh lớp đó là bội chung của 3; 4; 9

          3 = 3; 4 = 2²; 9 = 3²

BCNN(3; 4; 9) = 2².3² = 36

Vậy số học sinh của lớp đó thuộc bội của 36

          B(36) = {0; 36; 72; ...}

Vì số học sinh của lớp đó từ 30 đến 40 nên số học sinh lớp đó là:

       36 học sinh

Kết luận: Số học sinh của lớp đó là 36 học sinh.

A B C D E M N

Xét tư giác BCDE có

AD=AB (gt); AE=AC (gt) => BCDE là hình bình hành (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)

=> DE//BC (cạnh đối hbh) => DN//BM

Mà BM=DN (gt) 

=> BMDN là hbh (Tứ giác có 1 cawoj cạnh đối // và bằng nhau là hbh)

Nối MN cắt BD tại A' => A'D=A'B (Trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)

Mà AD=AB (gt); \(A\in BD;A'\in BD\)

\(\Rightarrow A'\equiv A\) hay A; M; N thẳng hàng

Ta có BMDN là hbh (cmt) => AM=AN (Trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)

Xét tg vuông ABC nếu

\(BM=CN\Rightarrow AM=\dfrac{BC}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)

Mà AM=AN (cmt)

\(\Rightarrow MN=AM+AN=\dfrac{BC}{2}+\dfrac{BC}{2}=BC\)

                      Giải:

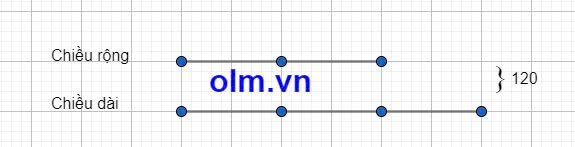
Nửa chu vi của hình chữ nhật là: 240 : 2 = 120 (m)

Ta có sơ đồ: 

Chiều dài là: 120 : (2+ 3)  x 3 = 72 (m)

Chiều rộng là: 120 - 72 = 48 (m)

Diện tích của hình chữ nhật là: 72 x 48 = 3456 (m²)

Đáp số: 3456 m²

3 số tự nhiên 0;1;2;3 nhé

làm được mình tick hết cho

Bài 3: Hình vẽ nào em ơi?

\(4x^3+12=120\)

\(4x^3=120-12\)

\(4x^3=108\)

\(x^3=108:4\)

\(x^3=27\)

\(x^3=3^3\)

\(Do\) \(đó\) \(x=3\)

Vậy \(x=3\)

KID KID

Câu 5:

a: A={0;1;2;3;...;20}

=>A={x\(\in\)N|x<=20}

b: Sửa đề: B={2;5;8;11;14;17;20}

=>B={x\(\in\)N|x=3k+2;0<=k<=6}

d: Sửa đề: D={2;6;12;20;30;42;56}

=>D={x\(\in\)N|x=k(k+1);1<=k<=7}

c: C={1;8;27;64;125}

=>C={x\(\in\)N|x=k³;1<=k<=5}

Câu 6:

a: tập hợp các số tự nhiên không lớn hơn 6 là:

A={0;1;2;3;4;5;6}

b: Các số tự nhiên có hai chữ số và không nhỏ hơn 90 là:

B={90;91;92;93;94;95;96;97;98;99}

c: Các số tự nhiên chia hết cho 3 mà lớn hơn 30; nhỏ hơn 50 là:

C={33;36;39;42;45;48}

d: 4:x=2

=>x=4:2=2(nhận)

=>D={2}

e: x+3<7

=>x<4

mà x là số tự nhiên

nên \(x\in\left\{0;1;2;3\right\}\)

=>E={0;1;2;3}

\(A=\dfrac{1}{2\times3}+\dfrac{1}{3\times4}+\dfrac{1}{4\times5}\)

\(A=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}\)

\(A=\dfrac{1}{2}-\dfrac{1}{5}\)

\(A=\dfrac{5}{10}-\dfrac{2}{10}=\dfrac{3}{10}\)