Chứng minh rằng với mọi số tự nhiên a, tồn tại số tự nhiên b sao cho ab + 4 là số chính phương.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


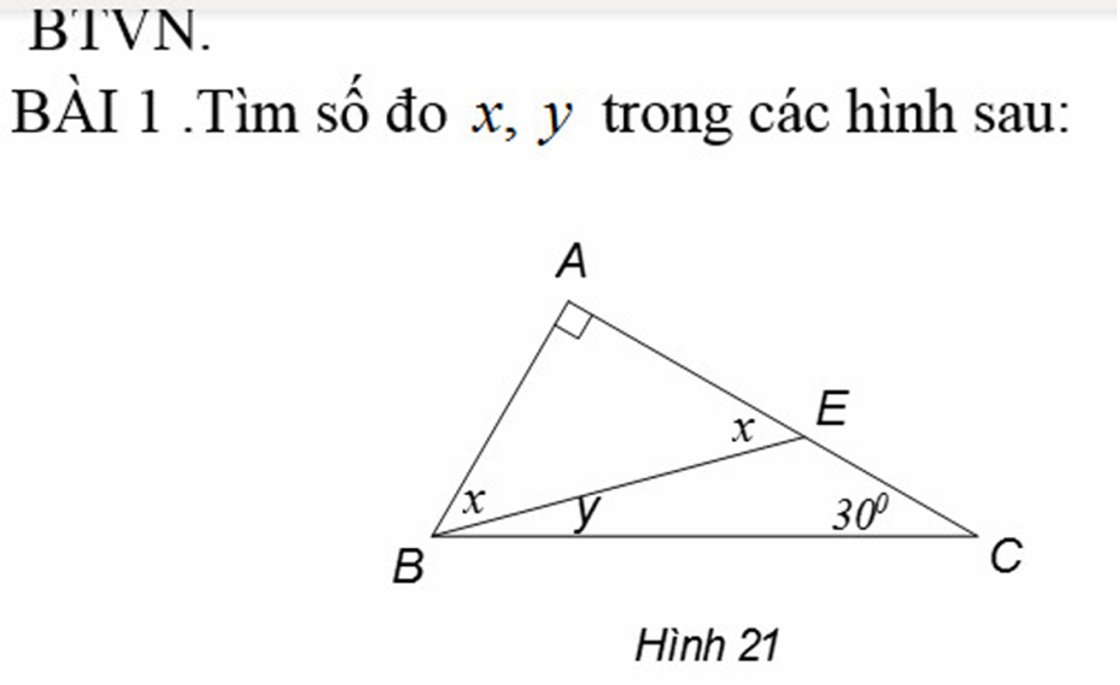
Tam giác ACE đều \(\Rightarrow AE=AC\) và \(\widehat{CAE}=60^o\)
Tam giác ABC vuông cân tại A \(\Rightarrow AB=AC\) và \(\widehat{BAC}=90^o\)
Từ đó \(\Rightarrow AE=AB\) \(\Rightarrow\Delta ABE\) cân tại A
Đồng thời \(\widehat{BAE}=\widehat{BAC}+\widehat{CAE}=90^o+60^o=150^o\)
\(\Rightarrow\widehat{ABE}=\dfrac{180^o-\widehat{BAE}}{2}=\dfrac{180^o-150^o}{2}=15^o\)
Mặt khác, tam giác ADB cân tại và \(\widehat{ADB}=150^o\) nên tam giác ADB chí có thể cân tại D (vì nếu cân tại điểm khác thì khi đó trong tam giác ADB sẽ có 2 góc bằng \(150^o\), vô lý). Khi đó \(\widehat{ABD}=15^o\)
Trên cùng 1 nửa mặt phẳng bờ là đường thẳng chứa tia BA, có \(\widehat{ABD}=\widehat{ABE}=15^o\) nên B, D, E thẳng hàng. (đpcm)

\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\\ \Rightarrow\dfrac{x+y}{xy}=\dfrac{1}{6}\\ \Rightarrow xy=6\left(x+y\right)\\ \Rightarrow xy-6x-6y=0\\ \Rightarrow x\left(y-6\right)-6\left(y-6\right)-36=0\\ \Rightarrow\left(y-6\right)\left(x-6\right)=36\)
Ta có bảng:
| y-6 | 36 | 1 | -1 | -36 | 2 | 18 | -2 | -18 | 3 | 12 | -3 | -12 | 4 | 9 | -9 | -4 | 6 | -6 | |||||
| x-6 | 1 | 36 | -36 | -1 | 18 | 2 | -18 | -2 | 12 | 3 | -12 | -3 | 9 | 4 | -4 | -9 | 6 | -6 | |||||
| y | 42 | 7 | 5 | -30 | 8 | 24 | 4 | -12 | 9 | 18 | 3 | -6 | 10 | 15 | -3 | 2 | 12 | 0 | |||||
| x | 7 | 42 | -30 | 5 | 24 | 8 | -12 | 4 | 18 | 9 | -6 | 3 | 15 | 10 | 2 | -3 | 12 | 0 |
Mà x,y nguyên dương nên (bạn tự chọn lại nhé)
`1/x + 1/y = 1/6`
`<=> (x+y)/(xy) = 1/6`
`<=> xy = 6x + 6y`
`<=> xy - 6x - 6y = 0`
`<=> x(y-6) - 6(y-6) = 36`
`<=> (x-6)(y-6) = 36`
Do `x-6, y-6 in ZZ` nên `(x-6) in Ư(36)`.
Đến đây bạn tự chia trường hợp và làm nhé.

Bài 7:
p là số nguyên tố lớn hơn 3
=>p=3k+1 hoặc p=3k+2
Nếu p=3k+1 thì \(8p+1=8\left(3k+1\right)+1=24k+9=3\left(8k+3\right)⋮3\)
=>Loại
=>p=3k+2
\(4p+1=4\left(3k+2\right)+1=12k+9=3\left(4k+3\right)⋮3\)
=>4p+1 là hợp số
Bài 6:
a: TH1: p=3
p+2=3+2=5; p+4=3+4=7
=>Nhận
TH2: p=3k+1
p+2=3k+1+2=3k+3=3(k+1)
=>Loại
TH3: p=3k+2
p+4=3k+2+4=3k+6=3(k+2)
=>Loại
b: TH1: p=5
p+2=5+2=7; p+6=5+6=11; p+18=5+18=23; p+24=5+24=29
=>Nhận
TH2: p=5k+1
p+24=5k+1+24=5k+25=5(k+5)
=>Loại
TH3: p=5k+2
p+18=5k+2+18=5k+20=5(k+4)
=>Loại
TH4: p=5k+3
p+2=5k+3+2=5k+5=5(k+1)
=>Loại
TH5: p=5k+4
p+6=5k+4+6=5k+10=5(k+2)
=>Loại
Vậy: p=5
Bài 5:
Với p=2 => 7p+5=7*2 + 5 = 19 (tm)
Với p>3
TH1: p=3k+1
=> 7(3k+1)+5=21k+7+5=21k+12=3(7k+4) ⋮ 3
=> 7p+5 là hợp số
TH2: p=3k+2
=>7(3k+2)+5=21k+14+5=21k+19
Vì p là số nguyên tố lớn hơn 3 => p lẻ => 3k + 2 lẻ => 3k lẻ => k lẻ
k lẻ => 21k lẻ => 21k + 19 chẵn => 21k+19 ⋮ 2
=> 7p+5 là hơn số
Vậy có p=2 là thỏa mãn

b: (2x+1):2=12:3
=>(2x+1):2=4
=>2x+1=2*4=8
=>2x=7
=>\(x=\dfrac{7}{2}\)
d: \(\dfrac{2x-14}{3}=\dfrac{12}{9}\)
=>\(\dfrac{2x-14}{3}=\dfrac{4}{3}\)
=>2x-14=4
=>2x=18
=>x=9

Câu 11:
\(C=\dfrac{\left|x-2017\right|+2018}{\left|x-2017\right|+2019}=\dfrac{\left|x-2017\right|+2019-1}{\left|x-2017\right|+2019}\\ =\dfrac{\left|x-2017\right|+2019}{\left|x-2017\right|+2019}-\dfrac{1}{\left|x-2017\right|+2019}\\ =1-\dfrac{1}{\left|x-2017\right|+2019}\)
Ta có: \(\left|x-2017\right|\ge0\forall x\Rightarrow\left|x-2017\right|+2019\ge2019\forall x\)
\(\Rightarrow\dfrac{1}{\left|x-2017\right|+2019}\le\dfrac{1}{2019}\forall x\)
\(\Rightarrow C=1-\dfrac{1}{\left|x-2017\right|+2018}\ge1-\dfrac{1}{2019}=\dfrac{2018}{2019}\)
Dấu "=" xảy ra khi: \(x-2017=0\Rightarrow x=2017\)
vậy: ...


1: Sửa đề: \(f\left(x\right)=3x\left(1-3x+2x^3\right)-2x^2\left(-4+3x^2-x\right)\)
\(=3x-9x^2+6x^4+8x^2-6x^4+2x^3\)
\(=2x^3-x^2+3x\)
\(g\left(x\right)=-4\left(x^4+x^2+1\right)+x^3\left(4x+2\right)+4\)
\(=-4x^4-4x^2-4+4x^3+2x^3+4\)
\(=2x^3-4x^2\)
Bậc là 3
Hệ số cao nhất là 2
Hệ số tự do là 0
2: f(x)=g(x)+h(x)
=>h(x)=f(x)-g(x)
\(=2x^3-x^2+3x-2x^3+4x^2=3x^2+3x\)
3: Đặt h(x)=0
=>3x(x+1)=0
=>x(x+1)=0
=>\(\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
1. `G(x)=-4(x^4+x^2+1)+x^3(4x+2)+4`
`=-4x^4-4x^2-4+4x^4+2x^3+4`
`=(4x^4-4x^4)+2x^3-4x^2+(4-4)`
`=2x^3-4x^2`
Bậc 3
Hệ số cao nhất: 2
Hệ số tự đó: 0
2. `F(x) = G(x) + H(x)`
`=>H(x)=F(x) - G(x)`
`=>H(x)=[3x(1-3x+2x^3)-2x^2(-4+3x^2-x)]-(2x^3-4x^2)
`=>H(x)=3x-9x^2+6x^4+8x^2-6x^4+2x^3-2x^3+4x^2`
`=>H(x)=3x^2+3x`
3. `H(x)=3x^2+3x=0`
`=>3x(x+1)=0`
TH1: `x=0`
TH2: `x+1=0=>x=-1`



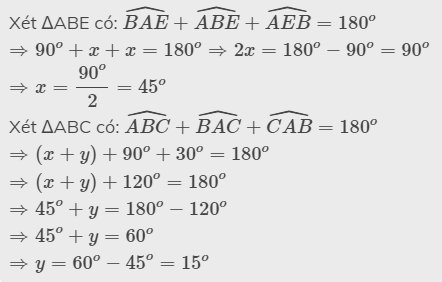
Giả sử tồn tại một số tự nhiên \(a\) để với mọi số tự nhiên \(b\), \(ab+4\) không phải là số chính phương. Điều này có nghĩa là phương trình \(ab+4=k^2\left(k\inℕ,k\ge2\right)\) không có nghiệm tự nhiên \(\left(b,k\right)\).
\(\Leftrightarrow b=\dfrac{k^2-4}{a}\) không có nghiêm tự nhiên.
Điều này tương đương với việc không tồn tại số tự nhiên \(k\) nào để \(k^2-4⋮a\). (*)
Ta sẽ chứng minh (*) vô lý.
Thật vậy, nếu \(a\ge4\) thì tồn tại số tự nhiên \(k=am+2\left(m\inℕ\right)\) thỏa mãn:
\(k^2-4=\left(am+2\right)^2-4=a^2m^2+4am+4-4=a\left(am^2+4m\right)⋮a\)
Nếu \(a=3\) thì tồn tại số \(k=3n+1\left(n\inℕ\right)\) để:
\(k^2-4=\left(3n+1\right)^2-4=9n^2+6n+1-4=9n^2+6n-3⋮3\)
Nếu \(a=2\) thì chỉ cần chọn \(k\) chẵn là xong.
Như vậy ta đã chỉ ra rằng (*) vô lý. Do đó điều ta giả sử ban đầu là sai.
Vậy ta có đpcm.