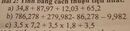\(\hept{\begin{cases}\left(x^2+y^2\right)\left(x-y\right)=13\\\left(x^2-y^2\right)\left(x+y\right)=25\end{cases}}\). Giair hệ phương trình
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
VT
1
2 tháng 12 2020
a,S=3^0+3^2+3^4+3^6+.....+3^2002
3^2xS=3^2+3^4+3^6+3^8+....+3^2004
(3^2-1)S=(3^2+3^4+3^6+....+3^2004)-(3^0+3^2+3^4+3^6+.....3^2002)
8S=3^2004-1
S=(3^2004-1)/8
b,Ta có : 3^2004-1=(3^6)^334-1=BS 3^6-1=BS 728
Mà 728 chia hết cho 7=>3^2004-1 chia hết cho 7
Mặt khác: ƯCLN(7;8)=1
=>S chia hết cho 7
2 tháng 12 2020
gọi hai số đó lần lượt là :a và b
theo bài ta có:a x 5x b :2=22,5
a x b x 5/2=22,5
a x b=9
vậy tích hai số bạn đầu là 9
2 tháng 12 2020
a,34,8+87,97+12,03+65,2
=(34,8+65,2)+(87,97+12,03)=100+100=200
b,786,278+279,982-86,278-9,982
=(786,278-86,278)+(279,982-9,982)
=700+200=900
2 tháng 12 2020
2 ta có x1+x2=1;x3+x4=1;...;x49+x50=1
mà x1+x2+x3+...+x50+x51=0
hay (x1+x2)+(x3+x4)+...+(x49+x50)+x51=0
1+1+1+1+..+1+x51=0(có 25 thừa số 1)
1*25+x51=0
25+x51=0
x51=0-25
x51=-254
3 Trong 31 số đã cho có ít nhất 1 số là số dương đó (vì nếu 31 số đã cho đêu âm thì tổng của 5 số bất kì không thể là 1 số dương)
Tách riêng số riêng đó ra còn 30 số , nhóm 5 số vào 1 nhóm thì được 6 nhóm . Trong đó nhóm nào cũng là 1 số dương .
⇒ Tổng của 30 số là 1 số dương cộng thêm 1 số dương đã tách .
Vậy tổng của 31 số đó là 1 số dương.