
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 4:
a: Xét ΔMAC và ΔMDB có
MA=MD
\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔMAC=ΔMDB
=>AC=BD
b: Ta có: ΔMAC=ΔMDB
=>\(\widehat{MAC}=\widehat{MDB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD
Ta có: AC//BD
AC\(\perp\)AB
Do đó: BD\(\perp\)BA
=>\(\widehat{ABD}=90^0\)
Bài 3:
Vì O là giao điểm của ba đường trung tuyến của ΔABC
nên O là trọng tâm của ΔABC
Gọi D là trung điểm của AC
Xét ΔABC có
O là trọng tâm
D là trung điểm của AC
Do đó: \(BO=\dfrac{2}{3}BD\)
=>BO=2OD
mà BO=OE
nên OE=2OD
=>D là trung điểm của OE
Xét ΔDAO và ΔDCE có
DA=DC
\(\widehat{ADO}=\widehat{CDE}\)(hai góc đối đỉnh)
DO=DE
Do đó: ΔDAO=ΔDCE
=>AO=CE

a; B = - 2\(x^2\) + 7\(x\) - 4
2B = - 4\(x^2\) + 14\(x\) - 8
C = A + 2B
C = 3\(x^2\) - 2\(x\) - 5 + (- 4\(x^2\) + 14\(x\) - 8)
C = 3\(x^2\) - 2\(x\) - 5 - 4\(x^2\) + 14\(x\) - 8
C = (3\(x^2\) - 4\(x^2\)) + (14\(x\) - 2\(x\)) - (5 + 8)
C = - \(x^2\) + 12\(x\) - 13
b; A = 3\(x^2\) - 2\(x\) - 5
3A = 9\(x^2\) - 6\(x\) - 15
D = 3A - 2B
D = 9\(x^2\) - 6\(x\) - 15 - (-4\(x^2\) + 14\(x\) - 8)
D = 9\(x^2\) - 6\(x\) - 15 + 4\(x^2\) - 14\(x\) + 8
D = (9\(x^2\) + 4\(x^2\)) - (6\(x\) + 14\(x\)) - (15 - 8)
D = 13\(x^2\) - 20\(x\) - 7

a) 7x³ - 5x + 2 - 4.(3x² - 2x - 4)
= 7x³ - 5x + 2 - 12x² + 8x + 16
= 7x³ - 12x² + (-5x + 8x) + (2 + 16)
= 7x³ - 12x² + 3x + 18
b) 5x.(-2x² - x + 1/15)
= -10x³ - 5x² + x/3
c) (3x + 2)(2x - 5)
= 6x² - 15x + 4x - 10
= 6x² + (-15x + 4x) - 10
= 6x² - 11x - 10

Câu 1:
a. Xét tam giác AED và ACB có:
AE = AC (gt)
Góc EAD = Góc CAB (2 góc đối)
AD = AB (gt)
=> hai tam giác bằng nhau (cgc)
b. CMtt tam giác EAB = tam giác CAD
=> Góc EBD = góc CDB (2 góc tương ứng)
Vị trí so le trong
=> EB // CD
Bài 1: Xét \(\Delta\) AED và \(\Delta\)ABC có: \(\left\{{}\begin{matrix}AE=AC\left(gt\right)\\AD=AB\left(gt\right)\\\widehat{EAD}=\widehat{BACđối}đỉnh\end{matrix}\right.\)
⇒ \(\Delta\) AED = \(\Delta\) ACB (c-g-c)
b; Tứ giác BCDE là hình bình hành vì có hai đường chéo cắt nhau tại trung điểm mỗi đường. ⇒ EB // DC (đpcm)

Giải:
Gọi số học sinh của mỗi nhóm lần lượt là: \(x;y;z\) (học sinh); \(x;y;z\)\(\in\)N*
Theo bài ra ta có:
4\(x\) = 6y = 12z và \(x+y+z\) = 42
4\(x\) = 6y ⇒ \(x\) = \(\dfrac{6}{4}\)y= \(\dfrac{3}{2}y\); 6y = 12z ⇒ z = \(\dfrac{6y}{12}\) = \(\dfrac{1}{2}\) y
Thay \(x=\)\(\dfrac{3}{2}y\); z = \(\dfrac{1}{2}y\) vào biểu thức: \(x+y+z\) = 42 ta có:
\(\dfrac{3}{2}y+y+\dfrac{1}{2}y=42\)
y.(\(\dfrac{3}{2}+1+\dfrac{1}{2}\)) = 42
y.3 = 42
y = 42 : 3
y = 14 (1)
thay y = 1 vào biểu thức: \(x\) = \(\dfrac{3}{2}y\) ⇒ \(x\) = 14.\(\dfrac{3}{2}=21\) (2)
Thay y = 14 vào biểu thức z = \(\dfrac{1}{2}y=\) 14.\(\dfrac{1}{2}\) = 7 (3)
Từ (1); (2); (3) ta có: \(\left(x;y;z\right)\) = (21; 14; 7)
Kết luận số học sinh tổ 1;tổ 2; tổ 3 lần lượt là: 21học sinh; 14 học sinh; 7 học sinh.
Gọi a (học sinh), b (học sinh), c (học sinh) lần lượt là số học sinh của nhóm I, nhóm II, nhóm III (a, b, c ∈ ℕ*)
Do năng suất trồng cây của mỗi học sinh là như nhau và cùng trồng một số cây như nhau nên số học sinh và số ngày hoàn thành là hai đại lượng tỉ lệ nghịch
⇒ 4a = 6b = 12c
⇒ a/3 = b/2 = c/1
Do tổng số học sinh là 42 nên a + b + c = 42
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
a/3 = b/2 = c/1 = (a + b + c)/(3 + 2 + 1) = 42/6 = 7
a/3 = 7 ⇒ a = 7.3 = 21 (nhận)
b/2 = 7 ⇒ b = 7.2 = 14 (nhận)
c/1 = 7 ⇒ c = 7.1 = 7 (nhận)
Vậy số học sinh của nhóm I, nhóm II, nhóm III lần lượt là: 21 học sinh, 14 học sinh, 7 học sinh

Vì \(2040⋮24\) nên ta chỉ cần chứng minh \(n^2-1⋮24\)
Do \(n\) là SNT > 3 nên \(n\) có dạng \(6k+1\) hoặc \(6k+5\)
TH1: \(n=6k+1\) thì \(n^2-1\)
\(=\left(n-1\right)\left(n+1\right)\)
\(=\left(6k+1-1\right)\left(6k+1+1\right)\)
\(=6k\left(6k+2\right)\)
\(=12k\left(3k+1\right)=A\)
Nếu k chẵn thì hiển nhiên \(A⋮24\). Nếu k lẻ thì \(3k+1⋮2\) \(\Rightarrow A⋮24\)
TH2: \(n=6k+5\)
\(\Rightarrow n^2-1=\left(n-1\right)\left(n+1\right)\)
\(=\left(6k+5-1\right)\left(6k+5+1\right)\)
\(=\left(6k+4\right)\left(6k+6\right)\)
\(=12\left(3k+2\right)\left(k+1\right)=B\)
Xét k lẻ thì \(k+1\) chẵn \(\Rightarrow B⋮24\)
k chẵn thì \(3k+2\) chẵn \(\Rightarrow B⋮24\)
Vậy \(n^2-1⋮24\) \(\Rightarrow n^2-1-2040⋮24\) \(\Rightarrow n^2-2041⋮24\) (đpcm)

\(\left(2x+1\right)\left(x-1\right)-\left(2x^2-x\right)=4\)
=>\(2x^2-2x+x-1-2x^2+x=4\)
=>-1=4(vô lý)
(2\(x\) + 1)(\(x\) - 1) - (2\(x^2\) - \(x\)) = 4
2\(x^2\) - 2\(x\) + \(x\) - 1 - 2\(x^2\) + \(x\) = 4
(2\(x^2\) - 2\(x^2\)) + (-2\(x\) + \(x\) + \(x\)) - 1 = 4
0 + 0 - 1 = 4
- 1 = 4 (vô lí)
Không có giá trị nào của \(x\) thỏa mãn đề bài
Vậy \(x\in\) \(\varnothing\)


Lời giải:
$x^3+x^2+x+1=2^y$
$\Rightarrow x^2(x+1)+(x+1)=2^y$
$\Rightarrow (x+1)(x^2+1)=2^y$
$\Rightarrow x+1=2^m; x^2+1=2^n$ với $m,n$ là số tự nhiên, $m+n=y$
$\Rightarrow (2^m-1)^2+1=2^n$
$\Rightarrow 2^{2m}-2^{m+1}+2=2^n$
Nếu $m,n$ đều $\geq 2$ thì hiển nhiên $2=2^n+2^{m+1}-2^{2m}\vdots 4$ (vô lý)
$\Rightarrow$ tồn tại ít nhất 1 trong 2 số nhỏ hơn 2.
Giả sử $n<2$. Khi đó $n=0$ hoặc $n=1$.
+ Nếu $n=0$ thì $x=0\Rightarrow m=0\Rightarrow y=m+n=0$ (tm)
+ Nếu $n=1$ thì $x=1\Rightarrow m=1\Rightarrow y=m+n=2$ (tm)

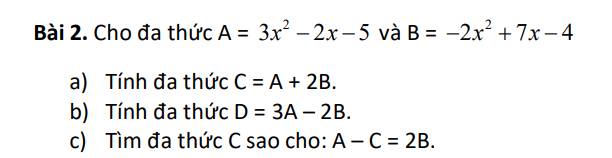
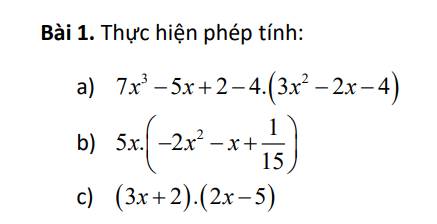


Ta có: BI+IC=BC
=>\(IC+\dfrac{1}{3}BC=BC\)
=>\(IC=\dfrac{2}{3}CB\)
Xét ΔCAD có
CB là đường trung tuyến
\(CI=\dfrac{2}{3}CB\)
Do đó: I là trọng tâm của ΔCAD
Xét ΔCAD có
I là trọng tâm
AI cắt DC tại K
Do đó: K là trung điểm của DC
=>DK=KC